- Home
- >
- Reflexive Property of Equality – Explanation and Examples
JUMP TO TOPIC
The Reflexive Property of Equality – Explanation and Examples
 The reflexive property of equality states that all real numbers are equal to themselves.
The reflexive property of equality states that all real numbers are equal to themselves.
While this important truth may seem obvious, it has far-reaching applications in arithmetic, logic, computer science, and algebra.
Before moving forward with this section, make sure to review the general article about the properties of equality.
This section covers:
- What Is Reflexive Property of Equality?
- Reflexivity and Equivalence Relations
- Reflexive Property of Equality Definition
- Example of Reflexive Property of Equality
What Is Reflexive Property of Equality?
The reflexive property of equality states that all numbers are equal to themselves.
This may seem incredibly obvious, so it is easy to think that it is not even worth mentioning.
On the contrary, this property ensures that equality is well-defined for proofs. It is also a good starting point for many proofs.
The English word “reflexive” comes from the Latin word “reflectere,” which means “to bend back” or “to turn back.” The reflexive property of equality means that equality “turns back on itself.” That is, it turns back on itself, like a reflection.
History of the Reflexive Property of Equality
Both Euclid and Peano articulated different versions of the reflexive property of equality in their own axiom lists.
Recall that axioms are statements that do not need to be proved. Reflexivity is a true axiom in that it does not immediately follow from other axioms. Despite the fact that it may seem obvious, it does ensure mathematical rigor. Therefore, most axiom lists include it.
Euclid only included a version of the axiom. Peano, however, included it for all natural numbers. Today, it is recognized that reflexivity holds for all real numbers.
Note that while reflexivity does not follow from other axioms, it can be used to deduce other truths commonly listed as axioms.
Reflexivity and Equivalence Relations
Equivalence relations are mathematical relationships that are symmetric, reflexive, and transitive. That is,
- If one element is related to a second, the second is also related to the first.
- Additionally, all elements are related to themselves.
- If two elements are each related to a third, then the first two are related to each other.
Since there are symmetric, reflexive, and transitive properties of equality, equality is an equivalence relation. Other examples of equivalence relations include triangle similarity and congruence.
Including the reflexive property of equality ensures that equality is well-defined as an equivalence relation. The concept is used in many proofs. For example, reflexivity and substitution together prove the transitive property of equality.
Why is this worth mentioning?
Not all relationships are reflexive. For example, comparisons are not all reflexive. There is no real number $a$ for which $a>a$ or $a<a$.
The reflexive property of equality also provides a good starting point for proofs. This is because beginning with $a=a$ or assuming $a=a$ is useful for many different types of proofs.
Reflexive Property of Equality Definition
The reflexive property of equality states that all real numbers are equal to themselves.
Euclid included a version of this property in his definition of Common Notion 4: “Things which coincide with one another are equal one another.” This is not exactly the same, but it is a useful articulation for geometric purposes.
Arithmetically, let $a$ be a real number. Then:
$a=a$
There is not an easily articulated converse of this. The contrapositive is similar to that of other properties of equality. Specifically, if $a$ and $b$ are real numbers such that $a \neq b$, then $b \neq a$.
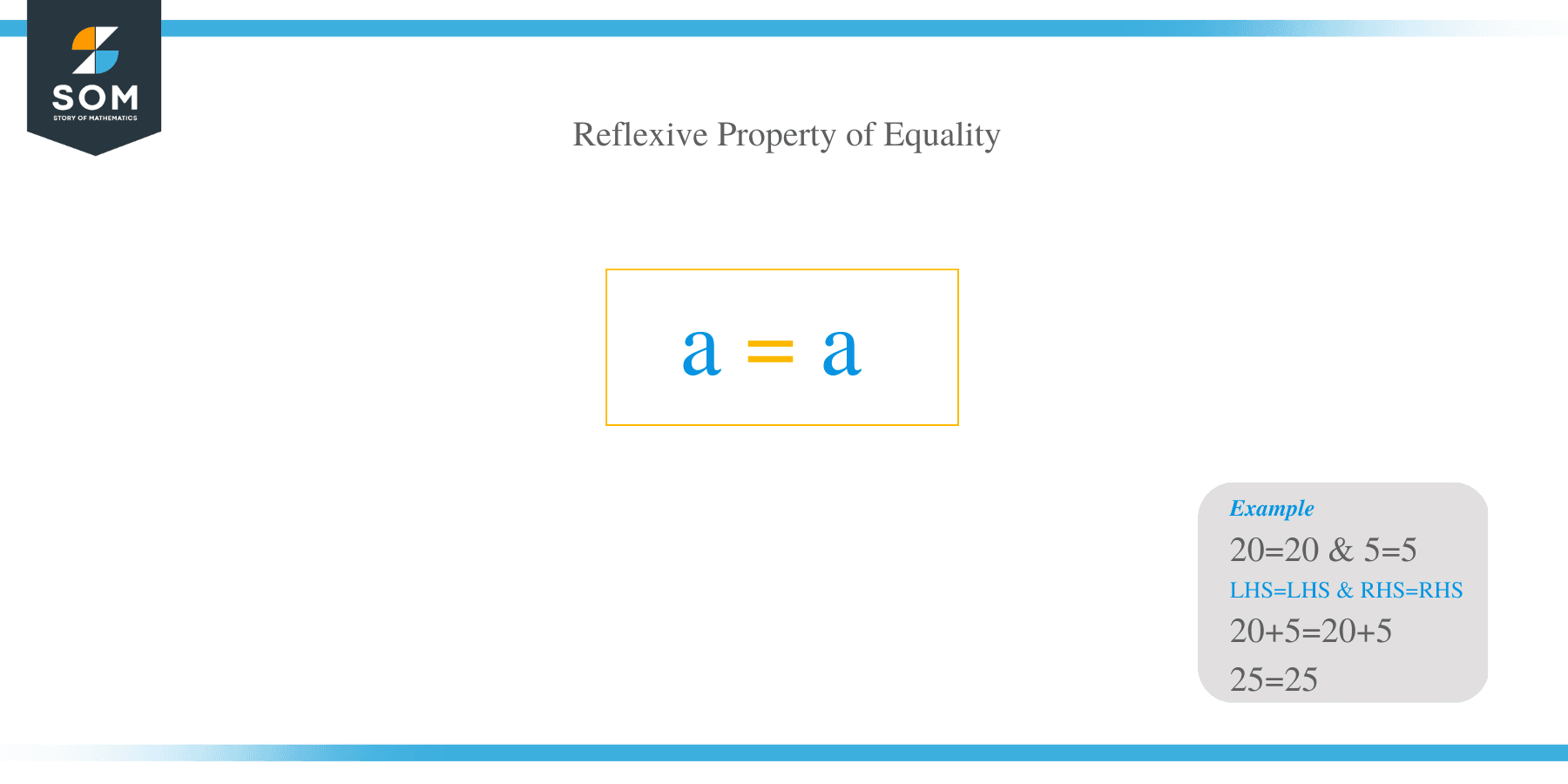
Example of Reflexive Property of Equality
Since Euclid did include a version of the reflexive property of equality, he used it in his proofs. One famous example is found in proposition 4. This proof establishes that two triangles with two equal sides and a common angle between the sides are the same.
The method Euclid uses to do this is called “superposition.” It is not a preferred proof method, but he mainly uses Common Notion 4 to support it.
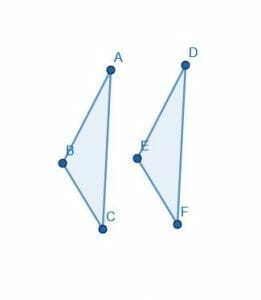
The proof begins with the assumption that $AB=DE$, $AC=DF$, and $\angle BAC= \angle EDF$.
Then, Euclid uses “superposition” to place triangle $DEF$ on $ABC$ so that $D$ lines up with $A$, $E$ lines up with $B$, and $F$ lines up with $C$.
Since $B$ lines up with $E$ and $C$ lines up with $F$, the line $BC$ lines up with $EF$. Therefore, since they are the same, Euclid states that they have equal length, invoking Common Notion 4.
He then notes that the whole triangle $ABC$ lines up with $DEF$ exactly. Using Common Notion 4, he concludes that the two are equal.
Common Notion 4 is only a version of the reflexive property, but other version prove fundamental facts about arithmetic.
Note that superposition was not Euclid’s preferred proof route. Additionally, even though he did not state the transitive property of equality, he used it in many proofs. This makes sense since it follows from the reflexive and substitution properties of equality.
Examples
This section covers common examples of problems involving the reflexive property of equality and their step-by-step solutions.
Note that in many cases, the reflexive property of equality works best as a starting point for a proof.
Example 1
Which of the following must be true?
A. $x$=$x$ for any real number $x$.
B. $7=7$.
C. $a+b+c=a+b+c$ for any real numbers $a, b,$ and $c$.
Solution
All three of these are true statements.
The first is a simple application of the reflexive property of equality. Any real number is equal to itself.
Similarly, since $7$ is a real number, $7=7$ by a basic application of the symmetric property of equality.
Finally, since $a, b,$ and $c$ are real numbers, $a+b+c$ is also a real number. Therefore, $a+b+c=a+b+c$.
Example 2
An athlete puts a twenty-pound weight and a five pound weight on the left side of a barbell. He then puts a twenty-pound weight and a five pound on the right side of the barbell. How does the weight on the left side of the barbell relate to the weight on the right side of the barbell?
Solution
The symmetric property of equality states that $20=20$ and $5=5$. The left side has $20+5=25$ pounds on it. On the right side, there is $20+5=25$ pounds. $25=25$ too.
Therefore, the weight on the left side of the barbell is equal to the weight on the right side of the barbell. This is guaranteed by the reflexive property of equality.
Example 3
Does the reflexive property of equality guarantee that if $a$ and $b$ are real numbers, then $a+b=b+a$?
Solution
Let $a$ and $b$ be real numbers. The reflexive property of equality states that $a=a$, $b=b$, $a+b=a+b$ and $b+a=b+a$.
The commutative property of addition states that $a+b=b+a$. This is not guaranteed by the reflexive property of equality.
Example 4
Prove that $2x+3x=3x+2x$ for any real number $x$ by beginning with $5x=5x$.
Solution
Let $x$ be a real number. The reflexive property of equality states that $x=x$ and $5x=5x$.
$5x=x+x+x+x+x$. It is possible to group the $x$ terms on the right side in various ways.
$x+x+x+x+x=2x+3x$
and
$x+x+x+x+x=3x+2x$
Therefore, $5x = x+x+x+x+x = x+x+x+x+x = 5x$ by the reflexive and symmetric properties of equality. By the substitution property then, $2x+3x=3x+2x$.
Note, this is similar to the proof of the transitive property of equality using the reflexive property of equality and the substitution property of equality.
Example 5
Use the reflexive property of equality to prove that $0$ is the additive identity.
Solution
Let $a$ be a real number and let $b$ be a real number such that $a+b=a$.
This means that $b$ is the additive identity.
Note that $a=a$ by the reflexive property of equality. The subtraction property of equality states that $a-a=a-a$. This simplifies to $0=a-a$.
Similarly, since $a+b=a$, the subtraction property of equality states that $a+b-a=a-a$.
The commutative property of addition states that $a+b-a=a-a+b$. This simplifies to $b$.
The right side of the equation simplifies to $0$. Therefore, $0+b=0$. In other words, $b=0$.
Thus, $0$ is the additive identity.
Images/mathematical drawings are created with GeoGebra
