Shell Method -Definition, Formula, and Volume of Solids

The shell method is an alternative way for us to find the volume of a solid of revolution. There are instances when it’s difficult for us to calculate the solid’s volume using the disk or washer method this where techniques such as the shell method enter.

In the cylindrical shell method, we utilize the cylindrical shell formed by cutting the cross-sectional slice parallel to the axis of rotation.  

In the past, we’ve learned how to calculate the volume of the solids of revolution using the disk and washer methods. After this article, we can now add the shell method in our integrating tools.

We’ll show you how to revolve a region under the curve and region bounded between two curves using the shell method. We’ll also do a quick comparison of the similarities and differences shared between the shell method and the two previous methods we’ve learned in the past.

For now, let’s understand what makes this technique unique and learn when it’s the best time to apply this method.

What is the shell method?

The shell method allows us to calculate the volume of the solid of revolution of regions that are challenging to calculate using the dish or washer method. In the past, we’ve learned how to approximate the volume by cutting it into “slices” perpendicular to the axis of rotation. This results in slabs that are cylindrical in shape or as we have learned in the past are shaped like disks or washers.

The shell method, however, requires a unique way of slicing the solid. In the shell method, the slices are obtained by cutting through the solid that is perpendicular to the axis of rotation. When that happens, we end up with concentric cylindrical shells hence, the name of this method.

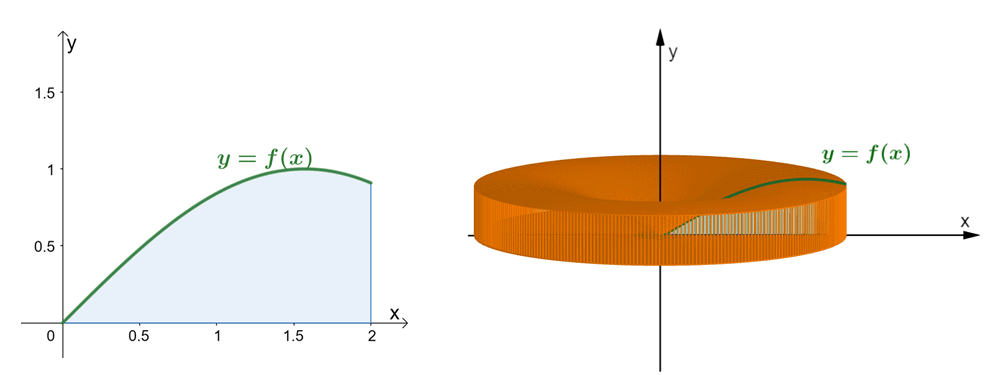
Take a look at the two graphs shown above. The graph on the left represents the curve of $y = \sin x$ and the area under its curve. The graph on the right showcases the solid formed by revolving the region around the $y$-axis. We can estimate the volume of the solid through the shell method. For now, let’s understand how the formula for the shell method was established.

Let’s begin by imaging that we have a paper label pasted on a cylindrical can with a radius, $r$, and a height of $h$. When we cut out the label from the can, we’ll see that the label will be rectangular in shaper with a length of $2\pi r$ and a height of $h$ as shown by the first pair of illustrations shown below.

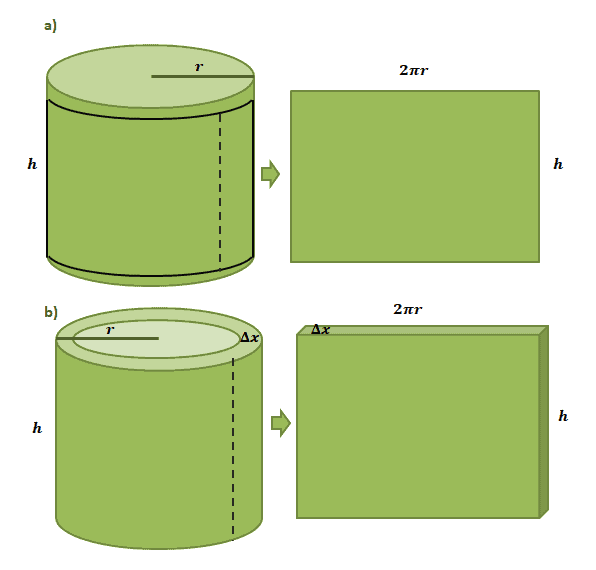
Estimating the volume of one cylindrical shell formed from the shell method follows the same process but this time, we’re using $\Delta x$ as its thickness. If we “cut” the shell out similar to the paper label, we’re expecting the resulting solid to have the following dimensions:

Now, let’s go back to the solid that we have broken down into $n$ cylindrical shells, we can estimate its total volume by adding the volumes of the $n$ cylindrical shells. In summation notation, we can express that as the equation shown below.

\begin{aligned}V &= \sum_{i =1}^{n} 2\pi r_i h_i \Delta x_i\end{aligned}

Let’s translate this in terms of $f(x)$ and $dx$ through the Riemann sum and the definition of definite integrals and we’ll now have the formal shell method formula.

Shell method formula

When we have a continuous and nonnegative function, $f(x)$, over the interval of $[a, b]$, we can rotate the region under its curve around the $y$-axis and end up with a solid made up of cylindrical shells that have the following dimensions:

• A radius that $x_i$ unit long.
• A height of $f(x_i)$.
• A thickness of $\Delta x_i$ or $dx$.

Each shell will have volume of $2\pi x_i f(x_i) \Delta x_i$. The solid’s volume can be estimated by adding each of cylindrical shell’s volume. Hence, we have the following:

\begin{aligned}V&\approx \sum_{i = 1}^{n} 2\pi x_i f(x_i)dx \\\\ V&= \lim_{n \rightarrow \infty}\sum_{i = 1}^{n} 2\pi x_i f(x_i)dx \\&= \int_{a}^{b} 2\pi x f(x) \phantom{x} dx\\ &= 2\pi \int_{a}^{b} x f(x) \phantom{x} dx \end{aligned}

This establishes the formula for the shell method when calculating the volume of the solid formed by revolving the region of $f(x)$ with respect to the $x$-axis.

Of course, there are instances when we need to revolve the solid with respect to the $y$-axis or when we’re working with regions bounded by two curves. This is why we’ve summarized the rest of the cases with their formulas in the table shown below.

Here are two more special cases to keep in mind: when we’re revolving the region with respect to the vertical axis, $x =h$, or the horizontal axis, $y =k$. Here’s how we calculate the resulting solid using the shell method.

We’ve actually covered all these types of solids in the past through our discussions on the disk method and the washer method. There are instances, however, that the shell method shines through. This is why for the next sections; we’ll show you instances when the shell method is more advantageous than the two other methods.

How to use the shell method?

Now that we have all four variations of the formula for the shell method, let’s break down the important steps to remember when applying this technique to calculate the volume of a solid.

• Sketch the area under the curve of the function or the region bounded by two functions.
• Set up a cylindrical shell as a guide and make sure that it is parallel with respect to the axis of rotation.
• Find the expression for the volume of the solid and simplify the integrand’s expression.
• Evaluate the definite integral using fundamental integral properties.

Let’s apply these pointers when finding the volume of the solid formed by $y= \dfrac{1}{x}$, $y = 0$, $x =1$, and $x =3$ with respect to the $y$-axis. First, graph the region bounded by these curves.     

Set up a cylindrical shell that is parallel to the axis of rotation. What happens in the shell method is that we revolve the infinitesimal cylindrical shells about the $y$-axis and have a solid that looks like the one on the right.

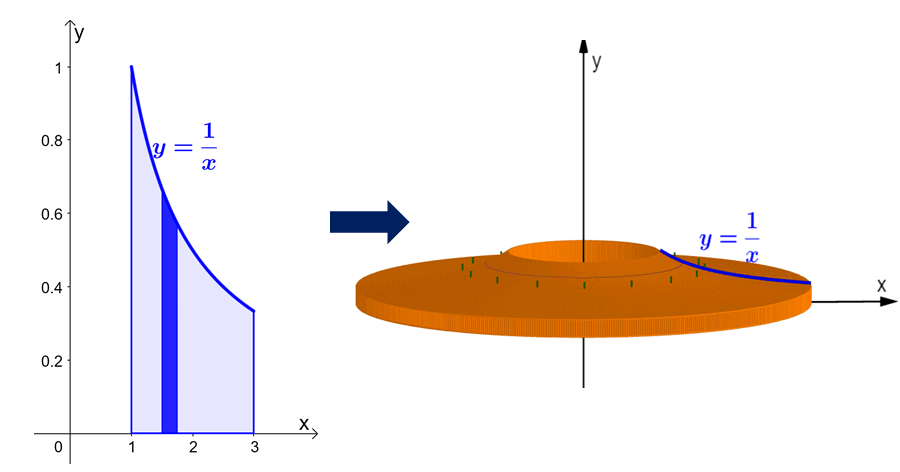
This means that we’re also evaluating $y = \dfrac{1}{x}$ with respect to $x$ and that  each cylindrical shell will have a thickness of $dx$. Since we’re working with one curve and a thickness of $dx$, we’ll use the default form of the formula: $V = 2\pi \int_{a}^{b} xf(x)\phantom{x}dx$, where $a = 1$ and $b =3$.

\begin{aligned}V &= 2\pi\int_{1}^{3} x \cdot \dfrac{1}{x} \phantom{x}dx\\&= 2\pi \int_{1}^{3} 1 \phantom{x}dx\\ &= 2\pi \left[x \right ]_{1}^{3}\\&= 2\pi(3 – 1)\\&= 4\pi\end{aligned}

This means that through the shell method, we have $V = 4\pi$. Meaning, the volume of the solid formed by revolving the area under the curve of $y = \dfrac{1}{x}$ from $x =1$ to $x =3$ is equal to $4\pi$.

When to use the shell method?

Although the disk and washer methods are more straightforward than the shell method, they may not be helpful when working with complex functions.

There are volumes of revolution that will require us to work on two or more integrals if we apply the washer method. When this happens, it’s much more convenient for us to apply the shell method instead.

For example, if we want to find the volume of the solid obtained by revolving the region bounded by the curves of $y = x^2 + 4$, $y =0$, $x=0$, $x =4$, and about the $y$-axis. To appreciate the simplicity of the shell method, let us show you how we revolve the region using the washer method versus the shell method.

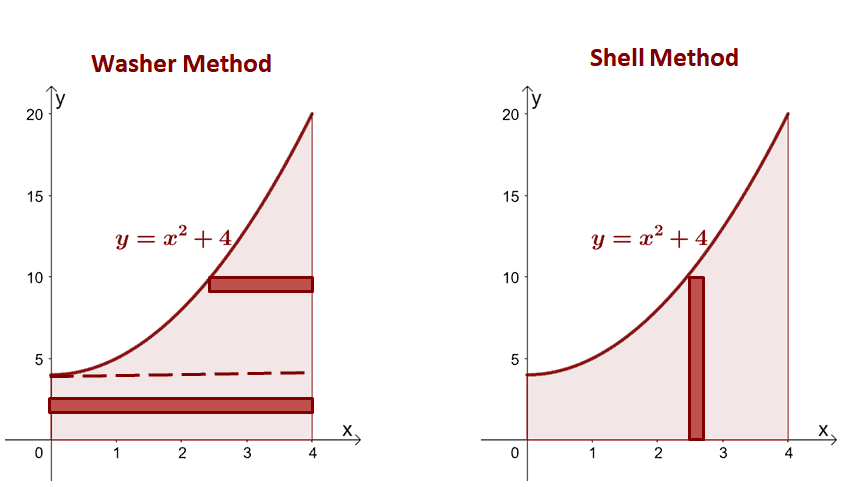
From this we can see that for washer method, we’ll have to rewrite the function in terms of $y$ first then divide the region into two regions: 1) region bound by $x =4$ to $x = \sqrt{y – 4}$ over the interval $[4, 20]$ ]and 2) region bound by $x=0$ and $x= 4$ from the interval $[0, 4]$. Meanwhile, for the shell method, we can see that all we need is to evaluate the integrate $x(x^2 + 4)$ with respect to $dx$ from $x=0$ to $x=4$.

Integrating the expressions obtained from the washer method will definitely be more tedious, so this highlights the importance of knowing the third technique: the shell method. The volume of the solid will still return the same values anyway, so always choose the method that requires less than and is more efficient.

Want to try out more problems that involve the shell method technique? Dive right into our next section to test your knowledge!

Example 1

Determine the volume of the solid formed by rotating the region bounded by $y = \sqrt{x}$, $y= 2$, and $x =0$ about the $x$-axis.

Solution

Sketch the region bounded by the curves and include a cylindrical shell as a guide. Keep in mind that when $x = 0$, $y = 0$ as well. Graph $y = \sqrt{x}$ from $y =0$ to $y = 2$.

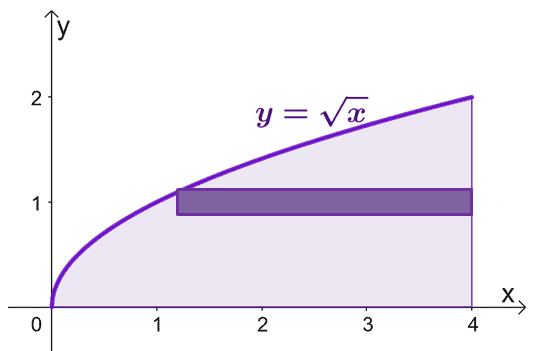
To estimate the area of the solid formed when we rotate the cylindrical shells about the $x$-axis, we can use the formula, $V = 2\pi \int_{a}^{b} y f(y) \phantom{x} dy$, from $y =0$ to $y=2$.

\begin{aligned}V &= 2\pi\int_{0}^{2} f(y) \phantom{x}dy\end{aligned}

We have $y = \sqrt{x}$, so as a function of $y$, we have $y^2 = x \Rightarrow f(y) = y^2$. Let’s evaluate the definite integral from $y =0$ to $y =2$.

\begin{aligned}V &= 2\pi\int_{0}^{2} y^2 \phantom{x}dy\\&= 2\pi \left[\dfrac{y^{2 +1}}{2 + 1}\right]_{0}^{2}\\&= 2\pi\left[\dfrac{y^3}{3}\right ]_{0}^{2}\\&= \dfrac{16\pi}{3}\end{aligned}

Here’s a visualization of how the solid would appear when the region under the curve of $y = \sqrt{x}$ is revolved about the $x$-axis.

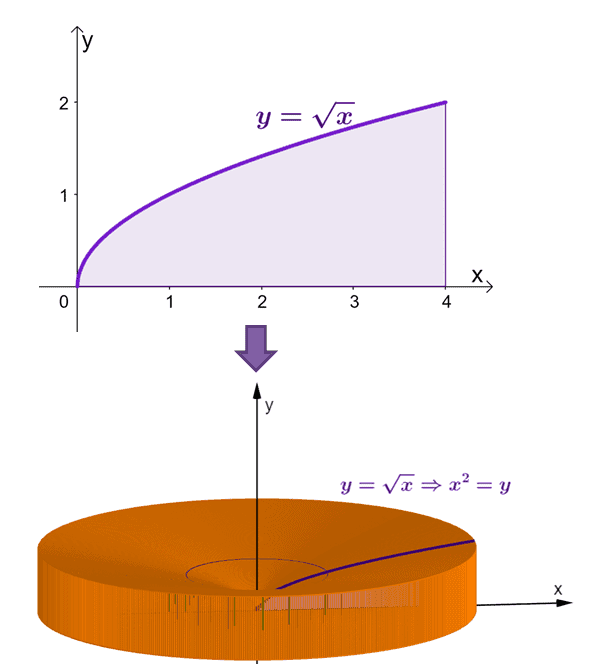
Through the shell method, we’ve calculated that the area of this solid is equal to $\dfrac{16\pi}{3}$ or approximately $16.755$.

Example 2

Determine the volume of the solid formed by rotating the region bounded by $y = x^4$, $y= 3x^3$, and about the vertical line, $x = -2$.

Solution

We’re now working with the region bounded by two curves: $y = 3x^3$ and $y = x^4$. the expressions to find the points of intersections shared between the two curves.

\begin{aligned}3x^3 &= x^4 \\x^4 – 3x^3 &=0\\x^3(x – 3)&= 0\\x&=0, 3 \end{aligned}

Let’s sketch the two curves and the region bound between the two. Include the vertical line, $x= -2$, as a reference. We’ve included the cylindrical shell as a guide too.

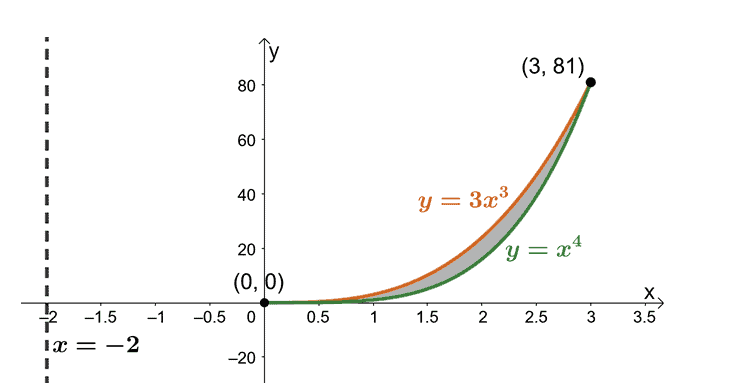
Find the volume of the solid using the formula, $ V = 2\pi \int_{a}^{b} (x – h)[f(x) – g(x)] \phantom{x} dx $. That’s because we’re rotating the region about the vertical line, $x= -2$. Hence, we have the following:

\begin{aligned}V &= 2\pi \int_{a}^{b} (x -h)[f(x)-g(x)] \phantom{x} dx\\&= 2\pi \int_{0}^{3} (x +2)[(3x^3) – (x^4)] \phantom{x}dx\\&= 2\pi \int_{0}^{3} (6x^3 + x^4 – x^5)\phantom{x}dx\\&= 2\pi \left[\dfrac{6x^{3 + 1}}{3 + 1} + \dfrac{x^{4 + 1}}{4 + 1} – \dfrac{x^{5 + 1}}{5 + 1} \right ]_{0}^{3}\\&= 2\pi \left[\dfrac{3x^4}{2} + \dfrac{x^5}{5}-\dfrac{x^6}{6} \right ]_{0}^{3}\\&= 2\pi\left(\dfrac{243}{5} \right )\\&= \dfrac{486\pi}{5}\end{aligned}

From this, we can see that the volume of the resulting solid of revolution is equal to $\dfrac{486\pi}{5}$ or approximately $405.363$.

Practice Questions

1. Determine the volume of the solid formed by rotating the region bounded by $y = \dfrac{x}{2}$, $y= 4$, and $x =0$ about the $y$-axis.

2. Calculate the volume of the solid formed by rotating the region bounded by $y = 3\sqrt{x}$, $y= 1$, and $x =0$ about the $x$-axis.

3. Determine the volume of the solid formed by rotating the region bounded by $y = x^2 + 4$, where $4 \leq x \leq 8$, and about the $y$-axis.

4. Calculate the volume of the solid formed by rotating the region bounded by $x= 2\sqrt{y}$, where $0 \leq y \leq 8$, and about the $y$-axis.

5. Determine the volume of the solid formed by rotating the region bounded by $y = \cos \pi x$, $y= \sin \pi x$, $x = \dfrac{1}{4}$, and $x =\dfrac{5}{4}$ about the $y$-axis.

Answer Key

1. The solid has a volume of $32\pi $ or approximately $100.531$.
2. The solid has a volume of $\dfrac{2\pi}{9} $ or approximately $0.698$.
3. The solid has a volume of $2112\pi$ or approximately $6635.044$.
4. The solid has a volume of $\dfrac{256\pi}{5}$ or approximately $160.850$.
5. The solid has a volume of $3\sqrt{2}$.

Images/mathematical drawings are created with GeoGebra.