• Home
  • >
  • Slopes of Parallel and Perpendicular Lines – Explanation & Examples

Slopes of Parallel and Perpendicular Lines – Explanation and Examples

Slopes of Parallel and Perpendicular LinesThe slopes of two parallel lines are the same, while the slopes of two perpendicular lines are the opposite reciprocals of each other.

Each line has infinitely many lines that are parallel to it and infinitely many lines that are  perpendicular to it. Before diving into the topic of parallel and perpendicular slopes, it is helpful to review the general concept of slope.

This section will cover:

  • What is the Slope of a Parallel Line?
  • How to Find the Slope of a Parallel Line
  • What is a Perpendicular Line?
  • What is the Slope of a Perpendicular Line?
  • How to find the Slope of a Perpendicular Line

What is the Slope of a Parallel Line?

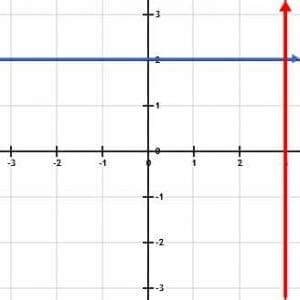
Parallel lines have the same angle of inclination. For example, the floor and the ceiling of a house are parallel to each other. The lines in the picture below are also parallel to each other.

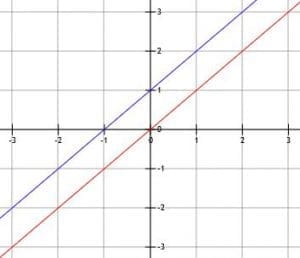
Parallel Lines with slope 1

Mathematically speaking, two lines are parallel if and only if they have the same slope. Two such lines will never intersect.

Note, however, that there are infinitely many lines that are parallel to a given line. This is because parallel lines can have different x and y-intercepts. Since there are infinitely many possible y-intercepts, there are infinitely many parallel lines.

How to Find the Slope of a Parallel Line

Finding the slope of a parallel line is pretty simple as long as we understand the definition of parallel lines and how to find slope generally.

We can distinguish two cases for finding the slope of a line parallel to a given line. Either we already know the slope of the given line or we do not know the slope of the given line.

Finding Parallel Lines When Slope is Known

If we know the slope of the given line, the slope of the parallel line is exactly the same.

In some cases, you may be asked to find the equation of a particular parallel line. If the y-intercept of this line is known, we can easily plug the slope and intercept values into the slope-intercept equation.

Alternatively, if another point other than the y-intercept is known, we can plug the values into the point-slope equation. Then, it is possible to solve for y, thus converting the equation into slope-intercept form.

Finding Parallel Lines When Slope is Not Given

In other cases, we may be given a line with a verbal description or graphical depiction without a given slope. If this is the case, we will have to solve for the slope before finding the slope of the parallel line or lines.

Recall that we can solve for the slope of a line as long as we know two points. Often, verbal descriptions will include these two points. For example, we may know that “a line passes through the points (1, 3) and (3, -4).”

Alternatively, we may have to find two points if we are given a graphical depiction of a line.

In either case, the formula for slope is:

m=(y1-y2)/(x1-x2).

Change in x and y

After we find the slope, we can proceed in the same way we did when the slope was known.

What is a Perpendicular Line?

Before discussing the slope of a perpendicular line, it is helpful to define a perpendicular line.

Two lines are perpendicular if they meet at a right angle.

For example, in the coordinate plane, the x and y-axes are perpendicular to each other.

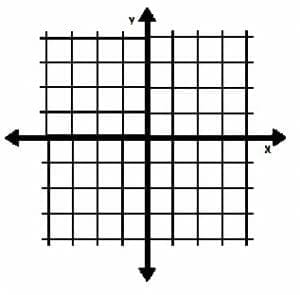
Simple Coordinate Plane

Just as there are infinitely lines parallel to any given line, there are infinitely many line perpendicular to a given line. This is because perpendicular lines will meet at exactly one point, and, for each point on a given line, there exists exactly one perpendicular line in two-dimensional space. Because there are infinitely many points on a line, each line consequently has infinitely many perpendicular lines.

Perpendicular lines

What is the Slope of a Perpendicular Line

If two lines are perpendicular, their slopes are the opposite reciprocals of each other.

Recall that the reciprocal of a number n is n-1. Alternatively, we can think of it as 1/n.

If n is a fraction p/q, then the reciprocal of n is q/p. This is because 1/p/q is equal to 1÷p/q=1/1×q/p=q/p.

The opposite reciprocal of a number is the reciprocal with the opposite sign. If the slope of a line is positive, then the slope of a perpendicular line is negative. On the other hand, if the slope of a line is negative, then the slope of the perpendicular line is positive.

How to Find the Slope of a Perpendicular Line

As is the case with parallel lines, it is much easier to find the slope of a line perpendicular to a given line if we already know the slope of the given line. If not, we have to find the slope first. As always, we do this by dividing the change in y-values for two points by the change in x-values for the same two points.

Once we know the slope, m, of a line, we know that any line perpendicular to it will have a slope that is the opposite reciprocal of m. That is, the slope will be -m-1.

Finding the Equation of a Perpendicular Line

Often, we must find the equation of a line perpendicular to a given line that intersects it at a given point. To do this, we first find the slope of the perpendicular line. Then, we can plug the values for the slope and the intersection point into point-slope form. Finally, we can convert the point-slope form into slope-intercept form by solving for y.

But, what if we are given another point on the perpendicular line and asked where it intersects the given line?

As before, we can plug the values of the slope and the given point for the perpendicular line into the point-slope equation. Then, once we have the slope-intercept equation for the perpendicular line, we set it equal to the slope-intercept equation for the given line.

This works because we want to find the value of x that gives the same value of y regardless which of the two equations we use it in.

We will end up with an equation m1x+b1=m2x+b2.

Solving This Equation

To solve this, we subtract m2x from both sides and b1 from both sides. Doing this means all of the terms with x in them are on one side of the equation and all of the terms without x are on the other.

(m1-m2)x=b2+b1.

Now, dividing both sides by (m1-m2) leaves x by itself on one side of the equation. Therefore, b2+b1/(m1-m2) is the x-value of the point where the two lines intersect.

If we then plug this value into either original slope-intercept equation and solve, the answer will be the y-value of the point where the two lines intersect.

A Note About Undefined Lines

Remember that a vertical line has a slope that is undefined. How can we find a parallel or perpendicular line if the line does not have a slope?

As a general rule, if two lines both have undefined slope, they are both vertical lines. Their equation is x=a, where a is any real number. We can then consider all lines with this form of equation to be parallel. That is, all vertical lines are parallel to each other.

Again, it might seem impossible to find a line perpendicular to a line with an undefined slope. Likewise, it is also impossible to find the opposite reciprocal of a line with a slope of 0. We therefore consider all horizontal lines, which have slope of 0, to be perpendicular to all vertical lines.

This makes sense because the simplest example of parallel lines are the grid lines on the coordinate plane. Likewise, the simplest example of perpendicular lines are the x and y-axes on the coordinate plane.

vertical and horizontal lines

Examples

This section will cover common examples of problems involving the slopes of parallel and perpendicular lines. It will also include step-by-step solutions.

Example 1

The slope-intercept form of a line k is y=4/5x+6. What is the slope of any line parallel to k? What is the slope of any line perpendicular to k?

Example 1 Solution

Any line parallel to the line k will have the same slope. Since the equation is in slope-intercept form, we can easily find the slope, which is the coefficient of x. Therefore, both k and any parallel line will have a slope of 4/5.

Any line perpendicular to k will have a slope that is the opposite reciprocal of 4/5. To find this number, we simply change the sign and flip the fraction. Therefore, the slope of any line perpendicular to k is -5/4.

Example 2

A line l passes through the points (17, 2) and (18, 4). Find the equation of a parallel line that passes through the origin.

Example 2 Solution

In this case, the slope of the line l is not given. Using the formula for slope, we find that it is:

m=(4-2)/(18-17)=2/-1=-2.

Any line parallel to l will have the same slope.

This question specifically asks about a line that passes through the origin, (0, 0). This means that the y-intercept of this line is 0. Plugging the slope and intercept into the slope-intercept form tells us that the line is y=-2x.

Example 3

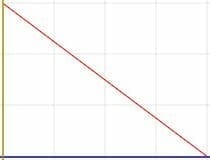
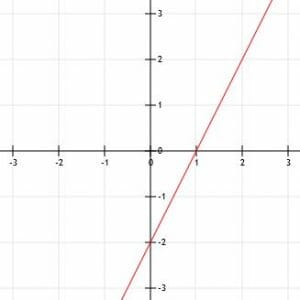
Find the equation of a line perpendicular to the line shown if the two lines have the same y-intercept.

Parallel and Perpendicular Lines Example 3

Example 3 Solution

Although we are given the intercept of the perpendicular line, we do not have the slope of the given line. To calculate it, we have to find two points on the graph. The x- and y-intercepts are easy to see, so we can use them. If (x1, y1) is (0, -2) and (x2, y2) is (4, 0), then the slope of the given line is:

m=(0+2)/(4-0)=2/4=1/2.

We know that the perpendicular line will have a slope that is the opposite reciprocal of the given line’s slope. If we flip the fraction 1/2 and change the sign, we have -2.

Since the y-intercept of the given line is also -2, the equation for the perpendicular line with the same y-intercept is y=-2x-2.

Note: This means that the two lines will intersect each other in the same place where they intersect the y-axis.

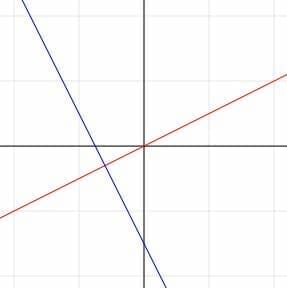
Example 4

The slope-intercept form of a line k is y=2/3x+1.

Another line, l, passes through the points (0, -1) and (3, 0).

A third line, n, is shown below:

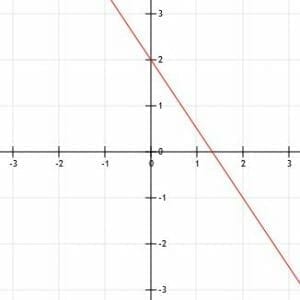
Parallel and Perpendicular Lines Example 4

Are the lines parallel, perpendicular, or neither?

Example 4 Solution

The easiest way to compare these three lines is to find their slopes.

Since k is already in slope-intercept form, we can easily find its slope. In this case, the coefficient of x, the slope, is 2/3.

The l passes through (0, -1) and (3, 0). We can therefore use the formula for slope to find the slope of this line.

m=(0+1)/(3-0)=1/3=1/3.

Finally, we have to find points on the line n using the graph. Its y-intercept is (0, 2), and another point is (2, -1). The slope formula tells us that the slope of n is:

m=(-1-2)/(2-0)=-3/2=-3/2.

Therefore, the slopes are 2/3, 1/3, and -3/2 for k, l, and n respectively.

None of the lines have the same slope, so none of them are parallel. The lines k and n, however, have slopes that are the opposite reciprocals of each other. Therefore, these two lines are perpendicular. The line l is unrelated to either of the other two.

Example 5

The slope-intercept form of a line k is y=9/4x-5. If l is perpendicular to k and passes through the point (9, -1), what is the equation of the line l and where do the two lines intersect?

Example 5 Solution

First, we have to find the slope of the line k so that we can find the slope of the line l. Since the equation for k is in slope-intercept form, its slope is the coefficient of x, 9/4.

Since l is perpendicular, its slope is the opposite reciprocal, -4/9.

We also know l passes through the point (9, -1). Using the known slope and point, we can plug the values for l into the point-slope formula:

y+1=-4/9(x-9).

We can simplify this further:

y+1=-4/9x+4

y=-4/9x+3.

This is the slope-intercept form of l. We can see from the original equation for k that its y-intercept is -5. Likewise, we see that the y-intercept of l is 3. Therefore, the two do not intersect at the y-intercept.

Then where do they intersect? We can set the two equations equal to each other because we are looking for a point where the same x-value in both equations yields the same y-value in both equations.

Therefore, we have:

9/4x-5=-4/9x+3

Moving the x-values to the left side and the intercepts to the other side gives us:

97/36x=8.

And solving for x yields:

x=288/97.

Now, we can find the corresponding y-value by plugging this x-value into either equation. We’ll use the equation for k, but it doesn’t really matter:

y=9/4(288/97)-5

y=648/97-5.

This further simplifies to:

y=163/97.

Thus, the intersection point is (288/97,163/97).

As this example shows, sometimes the numbers are not always “clean,” whole numbers. Getting complicated fraction or decimal numbers for one or both terms in a coordinate pair does not necessarily mean it is incorrect. In fact, numbers from real world models are not often simple whole numbers.

Practice Questions

1. The line $k$ has a slope-intercept form of $y=\dfrac{1}{9}x+8$. The line $l$ is parallel to $k$. If both $l$ and $k$ cross the $y$-axis at $22$, what is the equation of line $l$?

2. The line $k$ has a slope-intercept form of $y=\dfrac{1}{9}x+8$. The line $n$ is perpendicular to $k$. If both $l$ and $k$ cross the $y$-axis at $22$, what is the equation of line $n$?

3. The line $k$ passes through the points $(4, 7)$ and $(7, 4)$. The line $l$ is parallel to $k$. If both $l$ and $k$ cross the $y$-axis at $10$, what is the equation of line $l$ in slope-intercept form?

4. The line $k$ passes through the points $(4, 7)$ and $(7, 4)$. The line $n$ is perpendicular to $k$. If both $l$ and $k$ cross the $y$-axis at $10$, what is the equation of line $n$ in slope-intercept form?

5. The line $k$ is shown below. The line $l$ is parallel to $k$, and the line $n$ is perpendicular to $k$. If both $l$ and $k$ cross the $y$-axis at $-7$, what is the equation of line $l$ in slope-intercept form?

Parallel and Perpendicular Lines Practice Problems 4

6. The line $k$ is shown below. The line $l$ is parallel to $k$, and the line $n$ is perpendicular to $k$. If both $l$ and $k$ cross the $y$-axis at $-7$, what is the equation of line $n$ in slope-intercept form?

Parallel and Perpendicular Lines Practice Problems 4

7. The line $k$ has the equation $y=-\dfrac{6}{7}x – 3$. Another line, $l$, passes through the points $(0, -1)$ and $(6, 6)$. A third line, m, has the equation 7x+6y=1.
Finally, a fourth line, $n$, is shown below:
Parallel and Perpendicular Lines Practice Problem 5 

Are the lines, $l$ and$n$ parallel to each other, perpendicular to each other, or neither?

8. The line $k$ has the equation $y=-\dfrac{6}{7}x – 3$. Another line, $l$, passes through the points $(0, -1)$ and $(6, 6)$. A third line, m, has the equation 7x+6y=1.
Finally, a fourth line, $n$, is shown below:
Parallel and Perpendicular Lines Practice Problem 5 

Are the lines, $l$ and$k$ parallel to each other, perpendicular to each other, or neither?

9. The line $k$ has the equation $y=-\dfrac{6}{7}x – 3$. Another line, $l$, passes through the points $(0, -1)$ and $(6, 6)$. A third line, m, has the equation 7x+6y=1.
Finally, a fourth line, $n$, is shown below:
Parallel and Perpendicular Lines Practice Problem 5 

Are the lines, $n$ and$k$ parallel to each other, perpendicular to each other, or neither?

10. The line $k$ has the equation $y=-\dfrac{6}{7}x – 3$. Another line, $l$, passes through the points $(0, -1)$ and $(6, 6)$. A third line, m, has the equation 7x+6y=1.
Finally, a fourth line, $n$, is shown below:
Parallel and Perpendicular Lines Practice Problem 5 

Are the lines, $m$ and$k$ parallel to each other, perpendicular to each other, or neither?

11. The line $k$ has the equation $y=-\dfrac{6}{7}x – 3$. Another line, $l$, passes through the points $(0, -1)$ and $(6, 6)$. A third line, m, has the equation 7x+6y=1.
Finally, a fourth line, $n$, is shown below:
Parallel and Perpendicular Lines Practice Problem 5 

Are the lines, $m$ and$n$ parallel to each other, perpendicular to each other, or neither?

12. A line $k$ passes through the points $(-6, -1)$ and $(-5, -8)$. The line $l$ is parallel to $k$ and passes through the point $(1, 2)$.  What is the equation of the line $l$ in slope-intercept form?

13. A line $k$ passes through the points $(-6, -1)$ and $(-5, -8)$. The line $n$ is perpendicular to $k$ and passes through the point $(1, 2)$ as well. What is the equation of the line $n$ in slope-intercept form?

14. A line $k$ passes through the points $(-6, -1)$ and $(-5, -8)$. The line $n$ is perpendicular to $k$ and passes through the point $(1, 2)$ as well. Which point do the lines $k$ and $n$ intersect?


 

Previous Lesson | Main Page | Next Lesson