The Substitution Property of Equality – Explanation and Examples

The substitution property of equality states that if two quantities are equal, then one can replace the other in any equation or expression.

This property is important for many arithmetic and algebraic proofs.

Please make sure that you have reviewed the general properties of equality before reading through this section, 

This article will cover:

• What Is Substitution Property of Equality
• Substitution Property of Equality Definition
  
• Converse of the Substitution Property
• Uses in Trigonometry
• History of the Substitution Property of Equality
• Example of Substitution Property of Equality

What Is Substitution Property of Equality

The substitution property of equality is a fundamental principle of arithmetic and algebra. It essentially permits algebraic manipulation. Formal logic also relies on the substitution property of equality.

Many other properties of equality follow from this one, including some considered “axioms.”

The word substitution comes from the Latin word substutus. This means put in place of.This is exactly what happens when one quantity replaces another in an equation.

Substitution works both ways. That is, the term on the left can replace the term on the right and vice versa.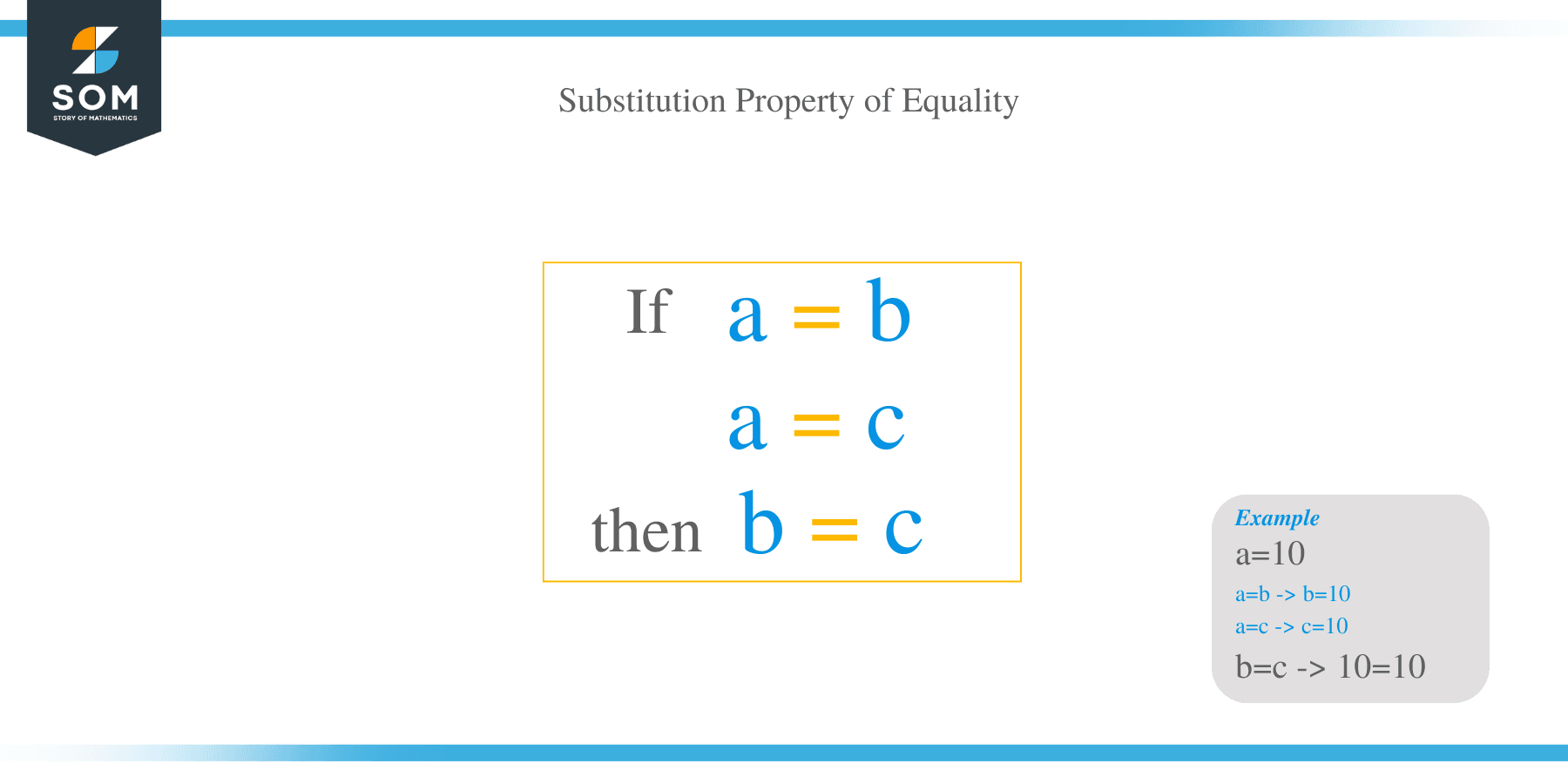

Substitution Property of Equality Definition

The substitution property of equality states that if two quantities are equal, then either can replace the other in any equation or expression.

That is, one can substitute for the other at any time.

Unlike other properties of equality, there is not a unique arithmetic formulation of the substitution property of equality. It is, however, possible to use function notation to describe it.

Let $x$ and $y$ be real numbers such that $x=y$. If $f$ is any real-valued function, then:

$f(x)=f(y)$

Converse of the Substitution Property

The converse is also true. That is, if two quantities are not equal, then one cannot replace another in any equation or expression without changing it.

Use in Trigonometry

This fact is incredibly useful in trigonometry as well for proving trigonometric identities. After a few trigonometric identities are known, it is easy to use substitution to prove other facts.

There are many relationships between trigonometric functions and their inverses. Example 3 uses the substitution property of equality and the transitive property of equality to prove that $cotx=\frac{cosx}{sinx}$. Practice Problem 3 uses the substitution property of equality to prove that $secx-sinxtanx=cosx$.

Uses in Verification

One of the goals of algebra is isolating a variable on one side of an equal sign to solve for it.

The substitution property of equality makes it easy to verify any solution. Simply substitute the solution back into the original equation anywhere the variable appears. Then, simplify to ensure that the two sides are still the same.

History of the Substitution Property of Equality

Euclid did not formally define the substitution property of equality or the transitive property of equality. He did, however, use both in his proofs.

Giuseppe Peano, an Italian mathematician who developed a list of axioms, defined the substitution property of equality. It was intended to ensure mathematical rigor as formalized math was taking off.

The substitution property is not an axiom as much as a rule of inference. This makes sense since it cannot be formulated arithmetically in the same way as some of the other properties of equality.

Substitution has always been important in formal logic. If any premises are connected by a biconditional statement, one can replace the other at any point.

Example of Substitution Property of Equality

The substitution property of equality is also useful in analyzing functions. One example is proving that an even function is even.

By definition, an even function, $f$, is one where $f(x)=f(-x)$ for any real number $x$ in the domain.

That is, substituting $-x$ for $x$ does not change the value of the equation. Using the substitution property makes it simple to verify whether a function is even or not.

For example, prove that $x^4+x^2+6$ is an even function.

If this is an even function, then $-x$ can be substituted for $x$ and the expression will stay the same.

$(-x)^4+(-x)^2+6=x^4+x^2+6$ because $(-x)^(2n)=x^(2n)$ for any natural number $n$.

Therefore, since $(-x)^4+(-x)^2+6=x^4+x^2+6$, $f(-x)=f(x)$. This means that $(-x)^4+(-x)^2+6$ is an even function.

Example 4 uses the substitution property of equality to verify an odd function.

Examples

This section covers common examples of problems involving the substitution property of equality and their step-by-step solutions.

Example 1

Let $a, b, c, d$ be real numbers such that $a=b$ and $c=d$. Which of the following are equivalent by the substitution property of equality?

A. $a+b=a^2$

B. $a-c=b-d$

C. $a+b+c+d=b+b+c+c$

Solution

A is not equal. This is because $a=b$, so $b$ can replace $a$ in any circumstance. Thus, $a+b=a+a=2a$. In general $2a\neq a^2$, so $a+b\neq a^2$.

B is equal. $a=b$, so $a-c=b-c$ by the substitution property. Then, because $c=d$, $b-c=b-d$ by the substitution property as well. Since $a-c=b-c$ and $b-c=b-d$. Thus, by the transitive property of equality $a-c=b-d$.

C is also equal. Since $a=b$, then $a+b+c+d=b+b+c+d$ by the substitution property of equality. Similarly, since $c=d$, $b+b+c+d=b+b+d+d$ also by the substitution property of equality. Thus, by the transitive property of equality $a-c=b-d$.

Example 2

A customer gives a cashier a one dollar bill and asks for change. The cashier gives her four quarters. After the exchange, the amount of money in the cashier’s cash drawer does not change. Why?

Solution

$1=0.25+0.25+0.25+0.25$. Therefore, the substitution property of equality states that four quarters can replace one dollar and vice versa.

The amount of money in the cash register drawer is equal to $c+0.25+0.25+0.25+0.25$. After the exchange takes place, there is $c+1$ in the drawer.

The substitution property of equality states that substituting $1$ for $0.25+0.25+0.25+0.25$ keeps the equality. Thus, the drawer has the same amount of money after the exchange.

Example 3

Prove that if $tanx=\frac{sinx}{cosx}$ and $cotx= \frac{1}{tanx}$, then $cotx= \frac{cosx}{sinx}$. Use the substitution property of equality.

Solution

Since $tanx=\frac{sinx}{cosx}$, $tanx$ can replace $\frac{sinx}{cosx}$ in any equation or expression.

Consider the equation:

$cotx= \frac{1}{tanx}$

Replace $tanx$ with $\frac{sinx}{cosx}$. Then:

$cotx= \frac{1}{\frac{sinx}{cosx}}$

This simplifies to

$cotx= \frac{cosx}{sinx}$

Therefore, according to the substitution property of equality, $cotx$ is equal to $\frac{cosx}{sinx}$.

Example 4

Odd functions are functions such that $f(x)=-f(x)$ for any real number $x$. Use the substitution property of equality to verify that $x^3-x$ is an odd function.

Solution

If $x^3-x$ is an odd function, replacing $x$ with $-x$ should yield $-(x^3-x)$.

Substituting $x$ with $-x$ yields:

$(-x)^3-(-x)$

This simplifies to:

$-x^3+x$

$-(x^3-x)=-x^3+x$

That is, $-(x^3-x)=-x^3+x$ and $(-x)^3-(-x)=-x^3+x$. Thus, applying the transitive property, $-(x^3-x)=(-x)^3-(-x)$. That is, $-f(x)=f(-x)$. Thus $x^3-x$ is an odd function according to the substitution and transitive properties of equality.

Example 5

Use the substitution property of equality to prove that if $6x-2=22$, then $x=4$.

Solution

The substitution property of equality states that if $x=4$, then $4$ can replace $x$ in any equation or expression.

Therefore, $4$ can replace $x$ in the equation $6x-2=22$ and it would still be true.

$6(4)-2=24-2=22$

Therefore, since $6(4)-2=22$ and $6x-2=22$, the transitive property of equality states that $6(4)-2=6x-2$.

Thus, by the substitution property $x$ is equal to $4$.

This process can be used to verify any solution to an algebraic problem.