Subtracting Fractions – Methods & Examples

How to Subtract Fractions?

Just like with addition of fractions, subtracting fractions with common denominators will just subtract the numerators and remain the denominator.

Similarly, with the case of fractions having unlike denominators, the least common multiple (LCM) should be get first then change the fractions into equivalent fractions with the LCM as the denominator. But these conditions are only applicable if the fractions are not mixed numbers.

Example 1

a. Solve: 2/5 – 1/4

Solution
First, make the denominators the same.

Multiply numerator and denominator of 2/5 and 1/4 by 4 and 5 respectively.

2/5× 4/4 = 8/20

1/4 x 5/5 = 5/20

Now do the subtractions:

8/20 − 5/20 =3/20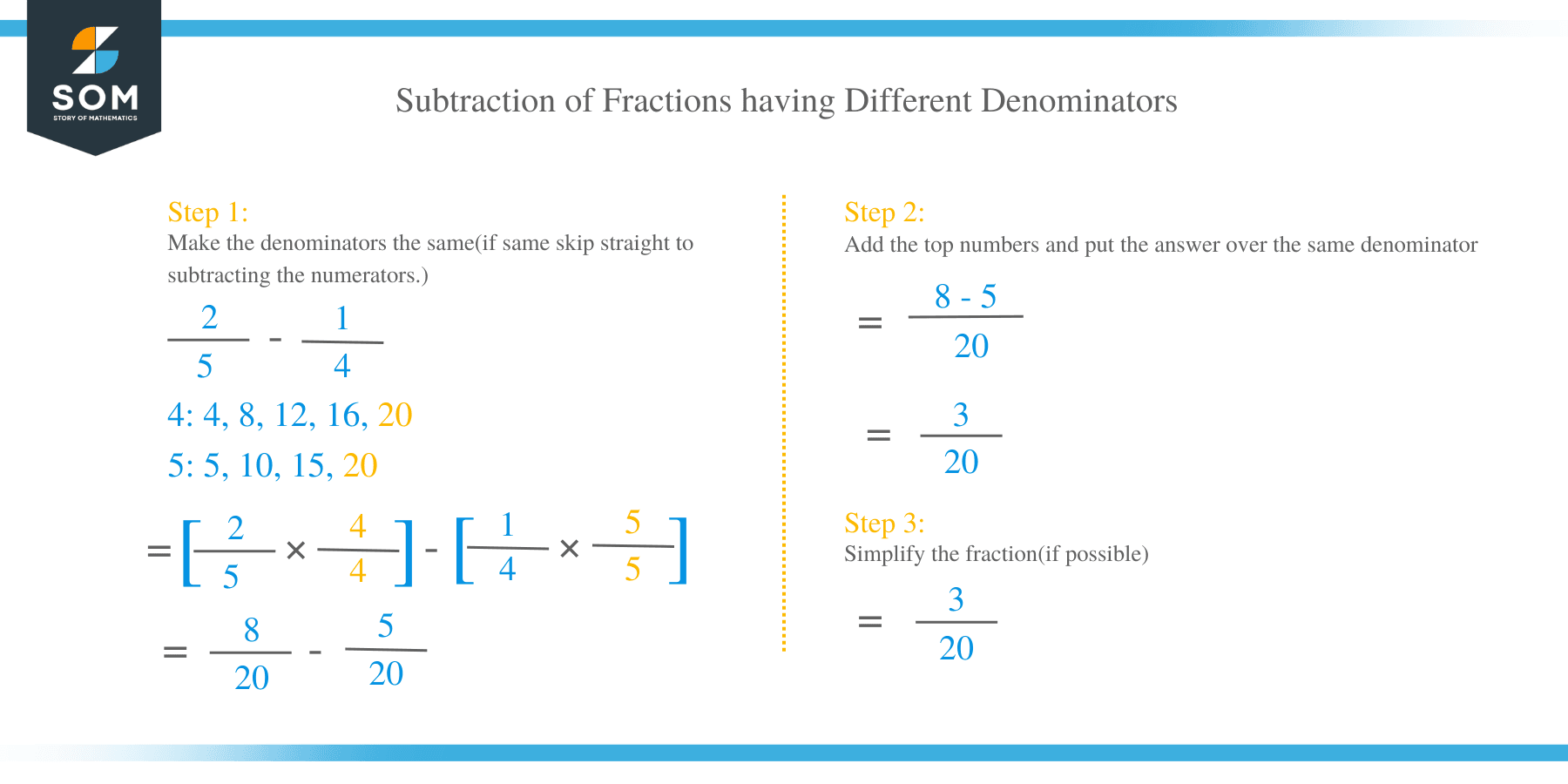

b. Subtract 3/8 from 7/8

Solution
7/8 – 3/8
= (7 – 3)/8

= 1/2

c. Subtract 5/6 from 11/6

Solution
11/6 – 5/6
= (11 – 5)/6
= 6/6
= 1/1
= 1

d. Subtract 7/9 from 11/9

Solution
11/9 – 7/9
= (11 – 7)/9
= 4/9

e. Subtract 4/6 from 16/6

Solution
16/6 – 4/6
= (16 – 4)/6

= 2/1

= 2

f. 1 – 2/3

Solution

• We start by assuming that a whole number is the same as the number over one i.e. 1 is 1/1

Therefore, our equation will look like this:

1/1-2/3

• We then continue to get the L.C.M. of the two denominators which will be 3 since the L.C.M. of a number and one becomes that number.
• We then divide this L.C.M. by the first denominator which is 1 to get the answer 3 then multiply 1 by the first numerator which is 1 to get =3
• We then divide the L.C.M. by the second denominator which is 3 to get the answer 1 then multiply 1 by the second numerator which is 2 to get =2
• We then subtract the two results above the L.C.M.

=1/1-2/3

= (3-2)/3

=1/3

How to Subtract Mixed Numbers?

Mixed fractions can be subtracted just like proper fractions. The rules for subtracting mixed factions are the same working with proper fractions. There are two methods to subtract mixed fractions.

Method 1:

The following are the steps taken when subtracting mixed fractions:

• First convert all the mixed fractions into improper fractions.
• Check whether the improper fractions have a common denominator, if not, find a common denominator for the fractions
• Try to create an equivalent fraction
• Subtract the numerator by keeping the denominator the same.
• If the result after subtraction is an improper fraction, convert it back into a mixed fraction or reduce it if it is a proper fraction

Example 2

6 ^1//₃ – 3 ¹/₁₂

= (6 × 3) + 1/3 + (3 × 12) + 1/12

= 19/3 – 37/12

= 19 × 4/3 × 4 – 37 × 1/12 × 1, (L.C.M. of 3 and 12 = 12)

= 76/12 – 37/12

= 76 – 37/12

= 39/12

= 13/4

= 3 ¼

Method 2

In this method, mixed fractions are split into wholes and parts.

• Subtract the whole parts of the fractions.
• Check whether the denominators of the fraction are same, and if not find a common denominator.
• Create equivalent fraction when necessary
• Subtract the numerators of fraction part by keeping the denominator same.
• Add the differences of whole number and fraction part together.

Example 3:

6 ¹/₃ – 3 ¹/₁₂

= (6 – 3) + (1/3 – 1/12)

= 3 + (1/3 – 1/12)

= 3 + (1 × 4/3 × 4 – 1 × 1/12 × 1) (L.C.M. of 12 and 3 = 12)

= 3 + 4/12 – 1/12

= 3 + (4 – 1)/12

= 3 + 3/12

= 3 + ¼

= 3 ¼

How to Subtract Fractions with Unlike Denominators?

Subtracting fractions with unlike denominators is very similar to adding fractions. When subtracting fractions with unlike denominators, it is important to calculate a common denominator for all the fraction. Then subtract the numerators by keeping the denominator constant.

• Choose a common denominator for the fractions by finding least common multiple of the denominators.
• Rewrite the fractions with the new common denominator.
• Subtract the numerator by keeping the denominator constant.

Example 4:
5/6 – 3/4
Solution:

• Find the LCM of 6 and 4 by listing their factors as shown below,
  4, 8, 12, 16, 20, 24, 28, 32, ….
  6, 12, 18, 24, 30, 36, 42, 48,.…
• In this case, the least common multiple of 4 and 6 is 12,
• Multiply each fraction by the LCM as:

5/6 = 5/6 x 2/2 = 10/12 and 3/4 = 3/4 x 3/3= 9/12.

• Now subtract the numerators, by keeping the denominators constant.

10/12 – 9/12 = 1/12

And hence 5/6 – 3/4 = 1/12

Example 5
4/5 – 1/3

Solution

• List multiples of 5 and 3.

5, 10, 15, 20, 25, 30,….
3, 6, 9, 12, 15, 18, 21,.…

From the multiples, the LCM of 3 and 5 is 15.

• Multiply by the LCM,

4/5 = 4/5 X 3/3 = 12/15 and 1/3 = 1/3 x 5/5 = 5/15

• Subtract numerators,

12/15 – 5/15 = 7/15

And thus,

4/5 – 1/3 = 7/15