JUMP TO TOPIC
Subtracting Mixed Numbers – Methods & Examples
A mixed number is a number that contains a whole number and a fraction, for instance 2 ½ is a mixed number.
How to Subtract Mixed Numbers?
We will learn in this article ways of subtracting mixed fractions or subtraction of mixed numbers. Subtraction of mixed fraction involves two methods.
Method 1
The first method entails:
- Subtracting whole numbers.
- Subtracting fractions by converting them first into like fractions.
- Adding the differences of whole numbers and like fractions.
Example 1
6 1/3 – 3 1/12
= (6 – 3) + (1/3 – 1/12)
= 3 + (1/3 – 1/12)
Find the L.C.M. of 12 and 3 as 12
= 3 + (1 × 4/3 × 4 – 1 × 1/12 × 1)
= 3 + 4/12 – 1/12
= 3 + (4 – 1)/12
= 3 + 3/12
= 3 + ¼
= 3 ¼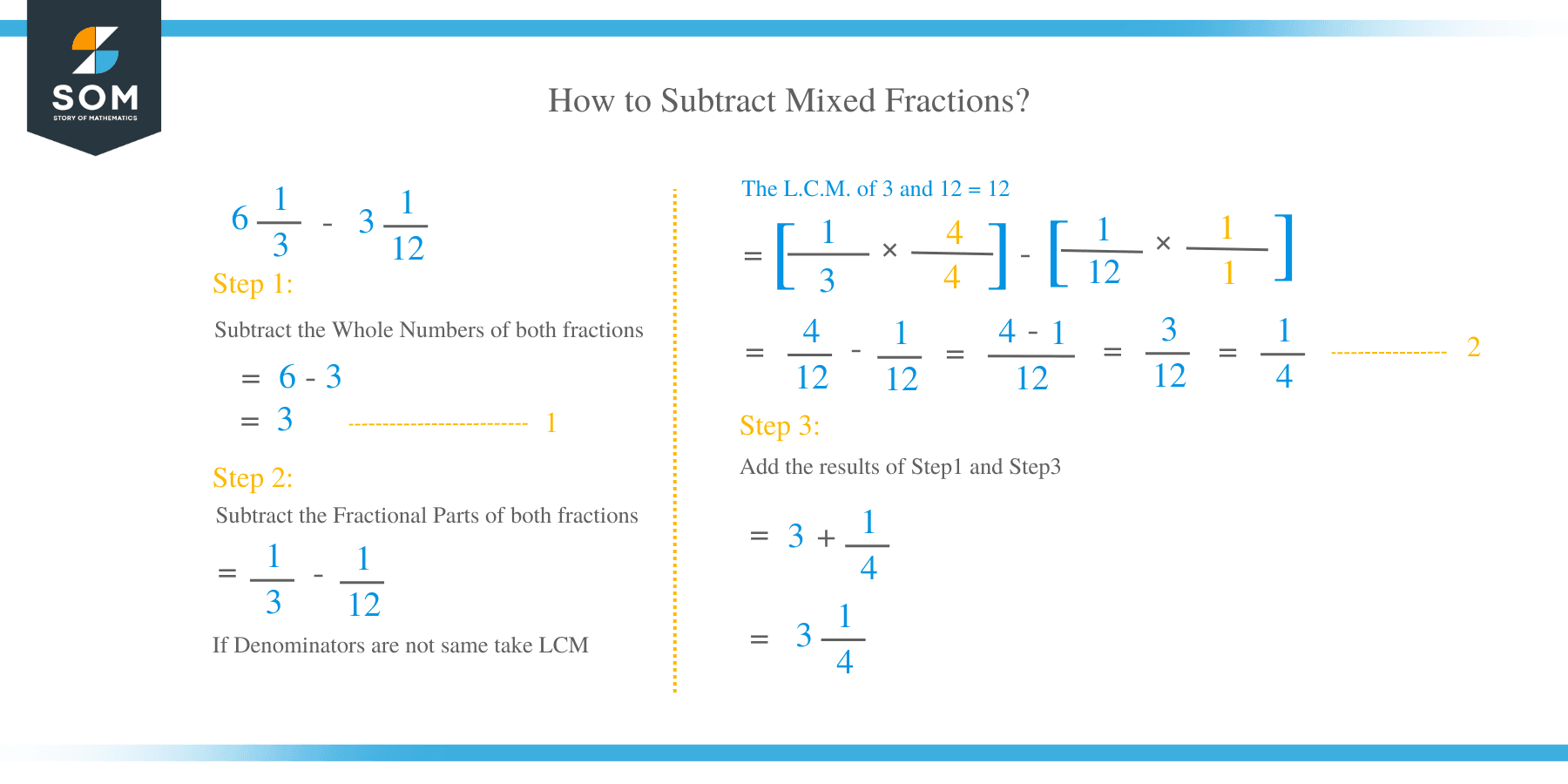
Method 2
The second method of subtracting mixed fractions involves:
- The first step is to convert mixed fractions into improper fractions
- Change the fractions into like fraction having a common denominator
- Now do the usual subtraction.
- Express the results into its lowest terms possible.
Example 2
Subtract: 6 1/3 – 3 1/12
= (6 × 3) + 1/3 + (3 × 12) + 1/12
= 19/3 – 37/12
The L.C.M. of 3 and 12 is 12
= 19 × 4/3 × 4 – 37 × 1/12 × 1
= 76/12 – 37/12
= 76 – 37/12
= 39/12
= 13/4
= 3 ¼
How to Subtract Mixed Fractions with Unlike Denominator?
Example 3
8 5/6 – 3 2/9
- The first procedure is to convert mixed fractions into improper fractions.
Multiply the whole number by the denominator of the fraction and then add the numerator. This number becomes the numerator of the improper fraction. The denominator of the improper fraction remains the same as the denominator of the mixed fraction.
{(6 x 8) + 5}/6 = 53/6
{(3 x 9) + 2}/9 =29/9
- Change the fractions to contain common denominators
The L.C. M of the fractions 9 and 6 = 18
53/6 = 159/18
29/9 = 58/18
- Multiplying the initial fraction by 3/3 and the second fraction by 2/2 will give out 18 for both denominators. You can notice that 3/3 and 2/2 are equal to 1, so we are actually doing is multiplication of both fractions by 1 and not altering the value of the fractions.
- Now perform the subtraction
159/18 – 58/18
- Subtract the numerators while maintaining the denominators
= (159 – 58)/18
= 101/18
= 5 11/18
More Examples with Solution
- Subtract:7 5/12 – 2 7/12
Solution
7 5/12 – 2 7/12
Since the fractional part have common denominators, to subtract the larger fraction part 7/12 from the smaller unit 5/12, borrow one.
7 5/12 = 6 + (1+ 5/12) = 6 17/12
Subtract whole numbers and fractions separately
(6 – 2) = 4
17/12 – 7/12
Subtract the numerators of fractions while maintaining the denominator
(17 – 7)/12 = 10/12
Simplify the fraction to its lowest terms possible
10/12 = 5/6
Add the fractional part to the whole number
(4 + 5/6) = 4 5/6
- At the end of a basketball match, the head coach realized that the a bottle of water, which was initially nine and three-eighths liters of water, had reduced down to three and nine-sixteenths liters. How many liters of water was consumed by the players?
Solution
Initial volume of water = nine and three-eighths = 9 3/8
Final volume of water = three and nine-sixteenths = 3 9/16
9 3/8 – 3 9/16
Convert the mixed fractions into improper fractions
9 3/8 = {(9 x 8) + 3}/8
= 75/8
3 9/16 = {(3 x 16) + 9}/16
= 57/16
Change the fractions to contain a common denominator.
The LCM of 8 and 16 is 16 , therefore,
75/8 = 150/16
And 57/16 =57/16
Subtract the fractions
150/16 – 57/16
Subtract the numerators while maintaining the denominators
(150 – 57)?16
=93/16
= 5 13/16
Therefore, liters of water were consumed by the players = 5 13/16
In summary, in-order to subtract mixed numbers:
If denominators are unlike, find Least Common Multiple of equivalent improper fractions. And if the first fraction less than the second fraction, you should borrow one unit from its whole number. Now subtract whole numbers and fractions separately. Find the sum of fraction difference and whole number difference. Simplify the final answer to its lowest terms possible.
