Subtraction Property of Equality – Explanation and Examples

The subtraction property of equality states that if a common value is subtracted from two equal quantities, then the differences are equal.

This fundamental fact is important to many branches of mathematics, including both arithmetic and algebra.

Before moving on with this section, make sure to review the general topic of properties of equality.

This section covers:

• What Is the Subtraction Property of Equality?
• Subtraction Property of Equality Definition
• Subtraction Property of Equality and Addition Property of Equality
• Example of Subtraction Property of Equality

What Is the Subtraction Property of Equality?

The subtraction property of equality states that equivalence holds when subtracting a common value from two or more equal quantities.

In arithmetic, this fact is helpful for finding equivalent values. In algebra, it is an important step used to isolate a variable and find its value. It also plays a crucial role in some geometric proofs.

Like other properties of equality, the subtraction property of equality may seem obvious. It is, however, necessary to define it because it ensures that all steps in a proof are logically valid and sound.

Mathematicians of antiquity knew and recognized the subtraction property of equality. In fact, Euclid referenced it so much that he gave it a name, common notion 3, in his Elements, which was written in the third century BC. He thought of it as axiomatic, or something that did not need to be proved true.

Later, in the 19th century, when focus on mathematical rigor took a front seat, Giuseppe Peano built his own list of axioms for natural numbers. He did not directly include the subtraction property of equality. Instead, addition, and, by extension, subtraction, usually augment his axioms.

The property is true beyond natural numbers; it is true for all real numbers.

Subtraction Property of Equality Definition

Euclid defined the subtraction property of equality as common notion 2 in his Elements: “If equals be subtracted from equals, then the differences are equal.”

In other words, if two quantities are equal and a common value is subtracted from each, the differences are still equal.

Arithmetically, if $a, b,$ and $c$ are real numbers, this is:

If $a=b$, then $a-c=b-c$.

The subtraction property of equality is true for all real numbers.

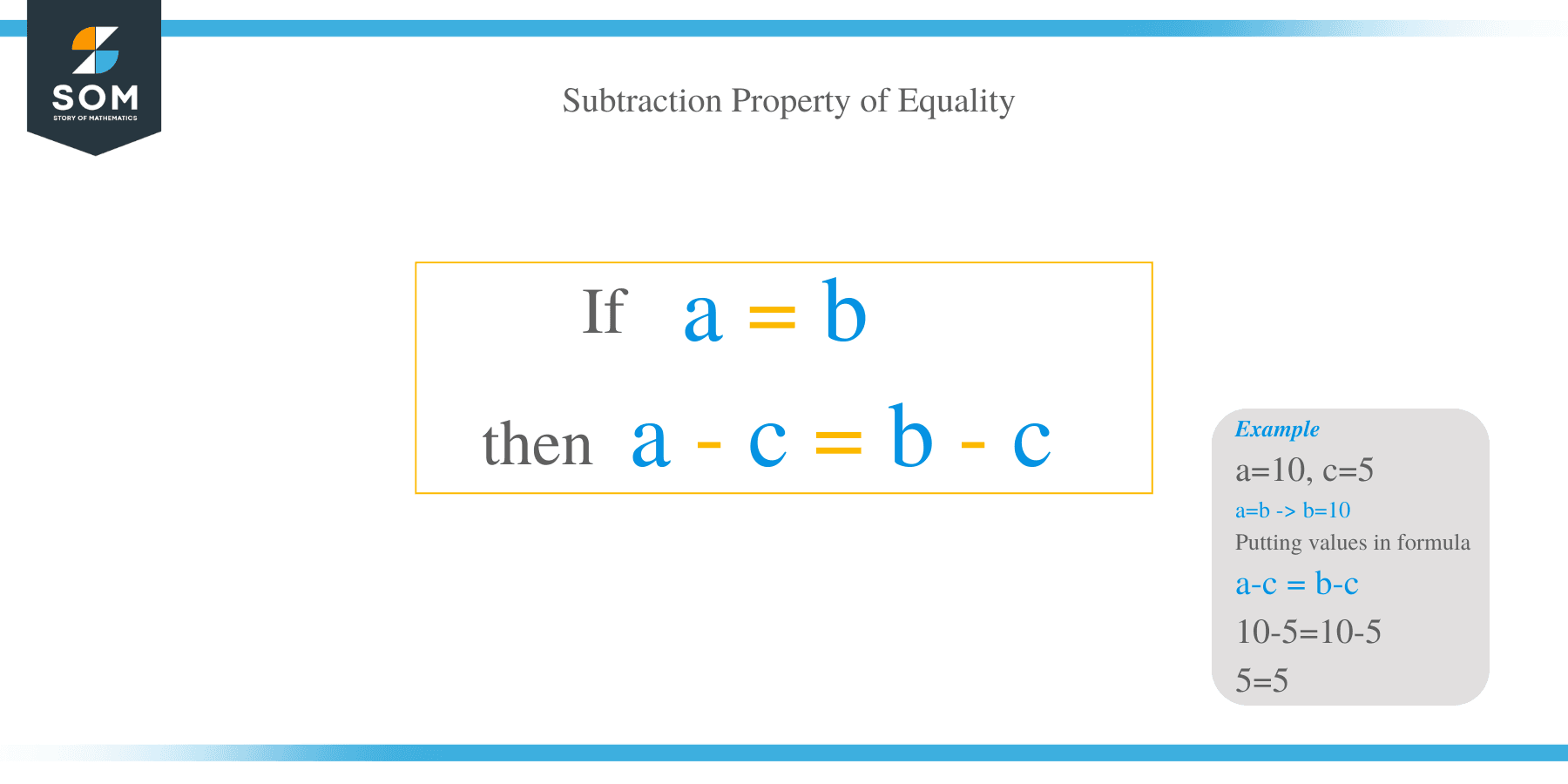
Subtraction Property of Equality and Addition Property of Equality

The subtraction property of equality and the addition property of equality are closely related.

Recall that the addition property of equality and the subtraction property of equality are both true for all real numbers. In particular, they are true for both positive and negative numbers.

Subtracting is the same as adding a negative, which means that it is possible to deduce the subtraction property of equality from the addition property of equality.

Likewise, subtracting a negative is the same as adding. Therefore, the addition property of equality can be deduced from the subtraction property of equality.

Why then, do most axiom lists (lists of things that do not need to be proved and can be assumed true) include both?

There are a couple reasons for this. First, historical lists, such as Euclid’s common notions and Peano’s axioms included both. This means historical proofs relied on the addition and subtraction axioms being separate.

Secondly, having a separate subtraction axiom helps in circumstances where negative values do not make sense. One example is geometric proofs, and another is proofs involving natural numbers.

Even though the property of equality holds for all real numbers, sometimes including all real numbers just does not make sense in context.

The example proof below is one of these cases. Additionally, example 3 includes a formal deduction of the addition property of equality from the subtraction property.

Example of Subtraction Property of Equality

An example of the subtraction property of equality comes from the proof for the construction of a copied line, shown here.

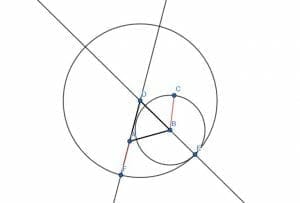
The proof shows that in the construction given, the constructed line AF is the same length as the given line BC. That is, AF=BC.

It does this by first noting that the lines DE and DF are both radii of the circle with center D and radius DE. Therefore, DE=DF.

Then, since ABD is an equilateral triangle, it notes that AD=BD. This is because all the legs in an equilateral figure have the same length.

The proof then invokes the subtraction property of equality by stating that since DE=DF and AD=BD, DE-BD=DF-AD.

DE-BD leaves the line BE, and DF-AD leaves the line AF.

The proof ends with the transitive property. Since AE and BC are radii of the same circle, they are equal in length. If AE=AF and AE=BC, the transitive property states that BC=AF. This was the original goal of the proof.

Examples

This section covers common problems using the subtraction property of equality and their step-by-step solutions.

Example 1

If $a=b$ and $c$ and $d$ are real numbers, which of the following are equal?

• $a-c$ and $b-c$
• $a-d$ and $b-d$
• $a-c$ and $b-d$

Solution

The first two are equal by a straightforward application of the subtraction property of equality. Since $c$ is equal to itself and $a=b$, $a-c=b-c$. 

Likewise, since $d$ is equal to itself, $a-d=b-d$.

The third one is not necessarily equal be $c$ and $d$ are not necessarily equal. A counterexample is $a=4$, $b=4$, $c=2$, and $d=3$. In this case, $a=b$, but $a-c=4-2=2$ and $b-d=4-3=1$. $2\neq1$, therefore $a-c\neq b-d$.

Example 2

Two bags of flour have the same weight. If 8 ounces of flour are removed from each bag, how do the new weights of the bags compare to each other?

Solution

The bags still have the same weight.

Let $a$ be the weight of the first bag in ounces and $b$ be the weight of the second bag in ounces. We know that $a=b$.

Now, each bag has 8 ounces of flour removed. The remaining weight of the first bag is $a-8$ and the remaining weight of the second bag is $b-8$.

Since they have the same amount of weight removed, the subtractive property of equality tells us that $a-8=b-8$. That is, the bags still have the same weight.

Example 3

Let $x$ be a real number such that $x+5=17$. Use the subtraction property of equality to find the value of $x$.

Solution

The subtraction property of equality states that it is possible to subtract a common term from both sides of an equation.

To solve for $x$, it is necessary to isolate the variable. In this case, subtracting 5 from the left side of the equation will do that.

Subtract 5 from both sides of the equation to get:

$x+5-5=17-5$

Then, simplify.

$x=12$

Therefore, $x=12$.

The substitution property gives an opportunity to check this solution.

$12+5=17$

Example 4

Prove that the subtraction property of equality can be used to deduce the addition property of equality.

Solution

The subtraction property of equality states that if $a, b,$ and $c$ are real number such that $a=b$, then $a-c=b-c$. It is required to show that this also means $a+c=b+c$.

Note, that since $c$ is a real number, $-c$ is also a real number.

Therefore, if $a=b$, then $a-(-c)=b-(-c)$.

Subtracting a negative is the same thing as adding a positive, so this simplifies to $a+c=b+c$.

Therefore, for any real numbers $a, b,$ and $c$ such that $a=b$, $a+c=b+c$. This is the addition property of equality, as required. QED.

Example 5

Let $a, b,$ and $c$ be real numbers such that $a=b$ and $b=2+c$.

Use the subtraction property of equality and the transitive property of equality to show that $a-c=2$.

Solution

Since $a=b$ and $b=2+c$, the transitive property of equality states that $a=2+c$.

Now, according to the subtraction property of equality, it is possible to subtract $c$ from both sides while retaining the equality. That is

$a-c=2+c-c$

Since $c-c=0$, this simplifies to

$a-c=2+0$

This further simplifies to:

$a-c=2$

Thus, $a-c$ is also equal to $2$, as required. QED.

Images/mathematical drawings are created with GeoGebra.