Supplementary Angles – Explanation & Examples

What are Supplementary Angles?

Supplementary angles are pairs angles such that the sum of their angles is equal to 180 degrees.

Although the angle measurement of straight is equal to 180 degrees, a straight angle can’t be called a supplementary angle because the angle only appears in a single form. For angles to be called supplementary, they must add up to 180° and appear in pairs.

Possibilities of a supplementary angle

• An acute and obtuse angle

A supplementary angle can be composed of one acute angle and another obtuse angle.

Illustration:

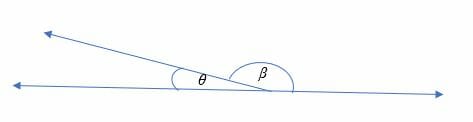
∠ θ and ∠ β are supplementary angles because they add up to 180 degrees. ∠ θ is an acute angle, while ∠ β is an obtuse angle.

∠ θ and ∠ β are also adjacent angles because they share a common vertex and arm.

An acute angle is an angle whose measure of degree is more than zero degrees but less than 90 degrees.

On the other hand, an obtuse angle is an angle whose measure of degree is more than 90 degrees but less than 180 degrees.

Common examples of supplementary angles of this type include:

⟹ 120° and 60°

⟹ 30° and 150°

⟹ 100° + 80°

⟹ 140° and 40°

⟹ 160° and 20° etc.

• Two right angles

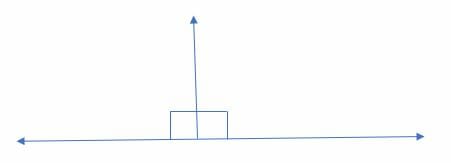
A supplementary angle can be made up of two right angles. A right angle is an angle that is exactly 90 degrees.

Illustration:

• Non-adjacent supplementary angles

Two pairs of supplementary angles don’t have to be in the same figure.

Illustration:

The two angles in the above separate figures are complementary, i.e., 140⁰ + 40⁰ = 180⁰

How to Find Supplementary Angles?

We can calculate supplementary angles by subtracting the given one angle from 180 degrees.  To find the other angle, use the following formula:

• ∠x = 180° – ∠y or ∠y = 180° – ∠x where ∠x or ∠y is the given angle.

Let’s work on the following examples.

Example 1

Check whether the angles 127° and 53° are a pair of supplementary angles.

Solution

127° + 53° = 180°

Hence, 127° and 53° are pairs of supplementary angles.

Example 2

Check if the two angles, 170°, and 19° are supplementary angles.

Solution

170° + 19° = 189°

Since 189°≠ 180°, therefore, 170° and 19° are not supplementary angles.

Example 3

Given two supplementary angles as: (x – 2) ° and (x + 5) °, determine the value of x.

Solution

The sum of the angles must be equal to 180 degrees: (x – 2) + (2x + 5) = 180

⟹ x – 2 + 2x + 5 = 180

⟹ x + 2x – 2 + 5 = 180

⟹ 3x + 3 = 180

⟹ 3x + 3 – 3 = 180 — 3

⟹ 3x = 180 — 3

⟹ 2x = 177

Divide both sides by 3 to get x as;

x = 59°
Therefore, the value of x is 59°.

Example 4

Calculate the value of θ in the figure below.

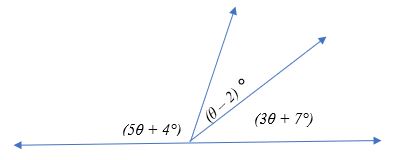
Solution

⟹ (5θ + 4°) + (θ – 2°) + (3θ + 7°) = 180°

⟹ 5θ + 4° + θ – 2° + 3θ + 7° = 180°

⟹ 5θ + θ + 3θ + 4° – 2° + 7° = 180°

⟹ 9θ + 9° = 180°

⟹ 9θ + 9° – 9° = 180° – 9°

⟹ 9θ = 171°

⟹ θ = 171/9

⟹ θ = 19°

Example 5

The ratio of a pair of supplementary angles is 1:8. Find the two measures of the two angles?

Solution

Let r be the common ratio.

One angle will be r, and the other will be 8r

Therefore, r + 8r = 180.

9r = 180

r = 180/9

r = 20

Substitute r = 20 in the initial equations.

Hence, one angle is 20 degrees, and the other is 160 degrees.

Therefore, the angles 20 degrees and 160 degrees are the two supplementary angles.

Example 6

Determine the supplement angle of (x + 10) °.

Solution

⟹ (x + 10) ° = 180 ° – (x + 10) °

= 180° – 10° – x°

= (170 – x) °