Surface Area of a Cone – Explanation & Examples

Cone is another important figure in geometry. To recall, a cone is a three-dimensional structure having a circular base where a set of line segments, connecting all of the points on the base to a common point called the apex. It is shown in the figure below.

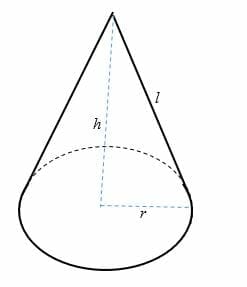
The vertical distance from the base center to the apex of a cone is the height (h), while the slant height of a cone is the length (l).

The surface area of a cone is the sum of the area of the slanted, curved surface and area of the circular base.

In this article, we will discuss how to find the surface area by using surface area of a cone formula. We will also discuss the lateral surface area of a cone.

How to Find the Surface Area of a Cone?

To find the surface area of a cone, you need to calculate the cone’s base and the lateral surface area.

Since the base of a cone is a circle, then the base area (B) of a cone is given as:

Base area of a cone, B = πr²

Where r = the base radius of the cone

Lateral Surface Area of a Cone

The curved surface of a cone can be viewed as a triangle whose base length is equal to 2πr (circumference of a circle), and its height is equal to the slanted height (l) of the cone.

Since we know, the area of a triangle = ½ bh

Therefore, the lateral surface area of a cone is given as:

Lateral surface area = 1/2×l×2πr

By simplifying the equation, we get,

The lateral surface area of a cone, (LSA) = πrl

Surface area of a cone formula

The total surface area of a cone = Base area + latera surface area. Therefore, the formula for the total surface area of a cone is represented as:

The total surface area of a cone = πr² + πrl

By taking πr as a common factor from RHS, we get;

Total surface area of a cone = πr (l + r) ………………… (Surface area of a cone formula)

Where r = radius of the base and l = slant height

By Pythagorean Theorem, the slant height, l = √ (h² + r²)

Solved Examples

Example 1

The radius and height of a cone are 9 cm and 15 cm, respectively. Find the total surface area of the cone.

Solution

Given:

Radius, r = 9 cm

Height, h = 15 cm

Slant height, l = √ (h² + r²)

l = √ (15² + 9²)

= √ (225 + 81)

=√306

= 17.5

Thus, slant height, l = 17.5 cm

Now substitute the values into the surface area of a cone formula

TSA = πr (l + r)

= 3.14 x 9 (9 + 17.5)

= 28.26 x 157.5

= 4,450.95 cm²

Example 2

Calculate the lateral surface area of a cone whose radius is 5 m and slant height is 20 m.

Solution

Given;

Radius, r = 5 m

Slant height, l = 20 m

But, the lateral surface area of a cone = πrl

= 3.14 x 5 x 20

= 314 m²

Example 3

The total surface area of a cone is 83.2 ft². If the slant height of the cone is 5.83 ft, find the radius of the cone.

Solution

Given;

TSA = 83.2 ft²

Slant height, l = 5 .83ft

But, TSA = πr (l + r)

83.2 = 3.14 x r (5.83 + r)

83.2 = 3.14 x r (5.83 + r)

By applying the distributive property of multiplication on the RHS, we get

83.2 = 18.3062r + 2.14r²

Divide each term by 3.14

26.5 = 3.14r + r²

r² + 3.14r – 26.5 = 0

r = 3.8

Therefore, the radius of the cone is 3.8 ft

Example 4

The total surface area of a cone is 625 in². If the slant height is thrice the radius of the cone, find the dimensions of the cone.

Solution

Given;

TSA = 625 in²

Slant height = 3 x radius of the cone

Let the radius of the cone be x

Slant height =3x

TSA = πr (l + r)

625 = 3.14x (3x + x)

Divide both sides by 3.14.

199.04 = x(4x)

199.04 = 4x²

Divide both sides by 4 to get

49.76 = x²

x = √49.76

x = 7.05

Therefore, the dimensions of the cone are as follows;

Radius of the cone = 7.05 in

Slant height, l = 3 x 7.05 = 21.15 in

Height of the one, h = √ (21.15² – 7.05²)

h = 19.94 in.

Example 5

The lateral surface area is 177 cm² less than the total surface area of a cone. Find the radius of the cone.

Solution

The total surface area of a cone = Lateral surface area + Base area

Therefore, 177 cm² = Base area

But, the base area of a cone = πr²

177 = 3.14r²

r² = 56.4 cm

r = √56.4

= 7.5 cm

So, the radius of the cone is 7.5 cm.

Example 6

The cost of painting a conical container is $0.01 per cm². Find the total cost of painting 15 conical containers of radius 5 cm and slant height 8 cm.

Solution

TSA = πr (l + r)

=3.14 x 5 (5 + 8)

= 15.7 x 13

= 204.1 cm²

The total cost of painting 15 containers = 204.1 x 0.01 x 15

= $30.62