Surface Area of a Cuboid – Explanation & Examples
Before we get started, let’s discuss what a cuboid is. A cuboid is one of the most common shapes in the environment around us. For example, a brick, a matchbox, a chalk box, etc., are all cuboids.
In geometry, a cuboid is a 3-dimensional figure with a length, width, and height. A cuboid has 6 rectangular faces. Ultimately, a cuboid has the shape of a rectangular prism or a box.
In a cuboid, the horizontal longer side is the length (l), and the shorter horizontal side is the width (w) or breadth (b). The height (h) of a cuboid is the vertical side.
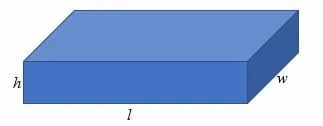
The surface area of a cuboid is the sum of the area of the 6 rectangular faces that cover it.
In this article, we will learn how to find the surface area using a cuboid formula’s surface area.
How to Find the Surface Area of a Cuboid?
To find the surface area of a cuboid, you need to calculate the area of each rectangular face and then sum up all the areas to get the total surface area i.e.
- Area of the top and bottom face = lw+ lw = 2lw
- Area of the front and back face = lh+ lh = 2lh
- Area of the two side faces = wh+ wh = 2wh
The total surface area of a cuboid is equal to the sum of the face areas;
Surface area of cuboid = 2lw + 2lh + 2wh
Note: The cuboid’s total surface area is not the same as the lateral surface area of a cuboid. The lateral surface of a cuboid is the sum of the area of the rectangular faces excluding the top and bottom face;
Lateral surface area of a cuboid (LSA) = 2h (l +b)
Surface area of a cuboid formula
From the above illustration, the formula for the total surface area of a cuboid can be represented as:
Total surface area of a cuboid (TSA) = 2 (lw + wh + lh)
The units for the surface area of a cuboid are square units.
Let’s practice some example problems below.
Example 1
The dimensions of a cuboid are given as follows:
Length = 5 cm
Width = 3 cm
Height = 4 cm.
Find the total surface area of the cuboid.
Solution
By the formula,
Total surface area of a cuboid = 2 (lw + wh + lh)
Substitute.
TSA = 2(5 x 3 + 3 x 4 + 5 x 4)
= 2(15 + 12 + 20)
= 2(47)
= 2 x 47 = 94 cm2
Therefore, the total surface area of the cuboid is 94 cm2
Example 2
The surface area of a cuboid is 126 ft2. If the cuboid’s length and height are 6 feet and 3 feet, find the width of the cuboid.
Solution
Given;
Total surface area = 126 ft2
Length = 6 ft
Height = 3 ft
Therefore,
⇒126 = 2 (lw + wh + lh)
⇒126 = 2 (6w + 3w + 6 x 3)
⇒126 = 2(9w + 18)
⇒126 = 18 w + 36
Subtract by 36 on both sides and then divide by 18
90 = 18 w
w = 5
Therefore, the width of the cuboid is 5 feet.
Example 3
Given the dimensions of a cuboid as:
Length = 10 m
width = 5 width
Height = 9 m
By how much is the total surface area of the cuboid more than the lateral surface area?
Solution
Total surface area = 2 (lw + wh + lh)
= 2 (10 x 5 + 5 x 9 + 10 x 9)
= 2(50 + 45 + 90)
TSA = 2 x 185
=370 m2.
The lateral surface area of a cuboid = 2h (l + b)
= 2 x 9(10 + 5)
= 18 x 15
= 270 m2
Total surface area – lateral surface area = 370 – 270
= 100 m2
Therefore, the total surface area of the cuboid is 100 m2 more than the lateral surface area.
Example 4
The length and width of a cardboard are 20 m by 10 m, respectively. How many cuboids can be made from the cardboard if each cuboid must be 4 m long, 3 m wide, and 1 m high.
Solution
Area of the cardboard = l x w
= 20 x 10
= 200 m2
Total surface area of the cuboid = 2 (lw + wh + lh)
= 2 (4 x 3 + 3 x 1 + 4 x 1)
= 2 (12 + 3 + 4)
= 2 x 19
= 38 m2
The number of cuboids = area of the cardboard/total surface area of a cuboid
= 200 m/38 m2
= 5 cuboids
Example 5
Compare the total surface area of a cube of length 8 cm and a cuboid of length 8 cm, width, 3 cm, and height, 4 cm.
Solution
Total surface area of a cube = 6a2
= 6 x 82
= 6 x 64
= 384 cm2
Total surface area of a cuboid = 2 (lw + wh + lh)
= 2(8 x 3 + 3 x 4 + 8 x 4)
= 2(24 +12 + 32)
= 2 x 68
= 136 cm2
Therefore, the surface area of the cube is more than the surface area of the cuboid.
