Surface Area of a Pyramid – Explanation & Examples

Before we get started, let’s review what a pyramid is. In geometry, a pyramid is a three-dimensional solid whose base is any polygon, and the lateral faces are triangles.

In a pyramid, the lateral faces (which are triangles) meet at a common point known as a vertex. The name of a pyramid is derived from the name of the polygon forming its base. For example, a square pyramid, a rectangular pyramid, a triangular pyramid, a pentagonal pyramid, etc.

The surface area of a pyramid is the sum of the area of the lateral faces. 

This article will discuss how to find the total surface area and lateral surface area of a pyramid.

How to Find the Surface Area of a Pyramid?

To find the surface area of a pyramid, you have to get the area of the base, then add the area of the lateral sides, which is one face times the number of sides.

Surface of a pyramid formula

The general formula for the surface area of any pyramid (regular or irregular) is given as:

Surface area = Base area + Lateral area

Surface area = B + LSA

Where TSA = total surface area

B = base area

LSA = lateral surface area.

For a regular pyramid, the formula is given as:

The total surface area of regular pyramid = B + 1/2 ps

where p = perimeter of the base and s = slant height.

Note: Never confuse the slant height (s) and height (h) of a pyramid. The perpendicular distance from the vertex to the base of a pyramid is known as the height (h), while the diagonal distance from the pyramid’s apex to the edge of the base is known as the slant height (s).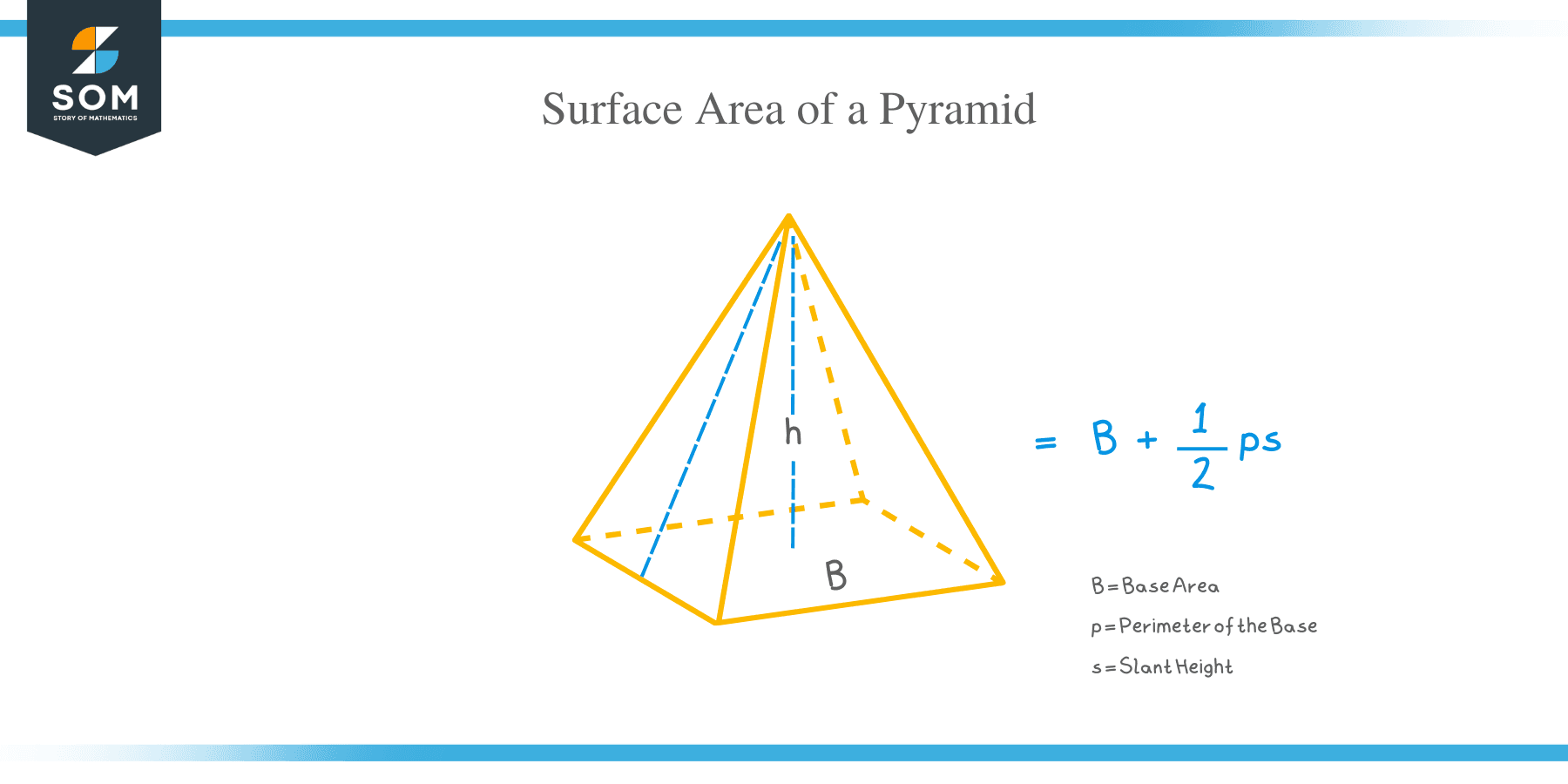

Surface area of a square pyramid

For a square pyramid, the total surface area = b (b + 2s)

Where b = the base length and s = slant height

Surface area of a triangular pyramid

The surface area of a triangular pyramid = ½ b (a + 3s)

Where, a = apothem length of a pyramid

b = base length

s = slant height

Surface area of a pentagonal pyramid

The total surface area of a regular pentagonal pyramid is given by;

Surface area of a pentagonal pyramid = 5⁄2 b (a + s)

Where, a = apothem length of the base

and b = side length of the base, s = slant height of the pyramid

Surface area of the hexagonal pyramid

A hexagonal pyramid is a pyramid with a hexagon as the base.

The total surface area a hexagonal pyramid = 3b (a + s)

Lateral Surface Area of a Pyramid

As stated earlier, the lateral surface area of a pyramid is the area of lateral faces of a pyramid. Since all the lateral faces of a pyramid are triangles, then the pyramid’s lateral surface area is half the product of the perimeter of the pyramid’s base and the slant height.

Lateral surface area (LSA = 1/2 ps)

Where p = perimeter of the base and s = slant height.

Let’s gain an insight into the surface area of a pyramid formula by solving a few example problems.

Example 1

What is the surface area of a square pyramid whose base length is 4 cm and slant height is 5 cm?

Solution

Given:

Base length, b = 4 cm

Slant height, s =5 cm

By the formula,

Total surface area of a square pyramid = b (b + 2s)

TSA = 4(4 + 2 x 5)

= 4(4 + 10)

= 4 x 14

=56 cm²

Example 2

What is the surface area of a square pyramid with a perpendicular height of 8 m and base length of 12 m?

Solution

Given;

Perpendicular height, h = 8 m

Base length, b =12

To get the slant height s, we apply the Pythagorean Theorem.

s = √ [8² + (12/2)²]

s = √ [8² + 6²]

s = √ (64 + 36)

s =√100

= 10

Hence, the slant height of the pyramid is 10 m

Now, calculate the surface area of the pyramid.

SA = b (b + 2s)

= 12 (12 + 2 x 10)

= 12(12 + 20)

= 12 x 32

= 384 m².

Example 3

Calculate the pyramid’s surface area, whose slant height is 10 ft, and its base is an equilateral triangle of side length, 8 ft.

Solution

Given:

Base length = 8 ft

Slant height = 10 ft

Apply the Pythagorean theorem to get the apothem length of the pyramid.

a = √ [8² – (8/2)²]

= √ (64 – 16)

= √48

a = 6.93 ft

Thus, the apothem length of the pyramid is 6.93 ft.

But, the surface area of a triangular pyramid = ½ b (a + 3s)

TSA = ½ x 8(6.93 + 3 x 10)

= 4 (6.93 + 30)

= 4 x 36.93

= 147.72 ft²

Example 4

Find the surface area of a pentagonal pyramid whose apothem length is 8 m, base length 6 m, and slant height is 20 m.

Solution

Given;

Apothem length, a = 8 m

Base length, b = 6 m

Slant height, s = 20 m

Surface area of a pentagonal pyramid = 5⁄2 b (a + s)

TSA = 5/2 x 6(8 + 20)

= 15 x 28

= 420 m².

Example 5

Calculate the total surface area and lateral surface area of a hexagonal pyramid with the apothem as 20 m, base length as 18 m, and slant height as 35 m.

Solution

Given;

apothem, a = 20 m

Base length, b =18 m

Slant height, s = 35 m

The surface area a hexagonal pyramid = 3b (a + s)

= 3 x 18(20 + 35)

= 54 x 55

= 2,970 m².

The lateral surface area of a pyramid =1/2 ps

Perimeter, p = 6 x 18

= 108 m

LSA = ½ x 108 x 35

= 1,890 m²