- Home
- >
- Symmetric difference – Definition and Examples
JUMP TO TOPIC
Symmetric Difference – Definition and Examples
 If you have been keeping up with the lessons, we’re confident you’re gradually progressing in your understanding.
If you have been keeping up with the lessons, we’re confident you’re gradually progressing in your understanding.
So far, we have covered several definitions, including the union of two sets, intersection, complement, etc. We have learned the difference between disjoint sets and intersecting sets. We have also discussed, at great length, what a universal set is.
Now, you’ll be learning a relatively complex lesson.
We presume you’re already familiar with the concept of operations on sets in which we construct a new set from an old one by performing some operation on it. We studied different operations that allowed us to construct a new set by picking certain elements, depending on our operation. These operations are well-defined as the union of sets, the intersection of sets, and the difference between sets.
Symmetric Difference is an operation not known to many. As the name suggests, it must be a variant of the difference between sets. The symmetric difference is an operation, so there must be operand sets. The symmetric difference is the derivative of all the topics that we have mentioned above.
Symmetric Difference is the set of elements from either of the operand sets, except for the intersection. It is also called a ‘disjunctive union.’
This is the most basic and generalized definition of this operation.
We will cover the following topics in this article:
- What is a symmetric difference?
- Notation of the symmetric difference
- The difference of sets vs. symmetric difference
- Venn Diagram Representation
- Properties
- Examples
- Practice Problems
Before moving forward, you may consider a quick refresher on the following prerequisites:
What is the Symmetric Difference?
We have discussed the logic of ‘AND’ and ‘OR’ in mathematics before. Understanding the ‘OR’ operation is crucial if we want to understand the symmetric difference better.
Concept of ‘or’ in Symmetric Difference:
In language, ‘or’ can be used exclusively or inclusively. When we say it is being used exclusively, we mean that we must choose one when presented with an option like juice or water. However, when we say it is being used inclusively, we can take juice, take water, or take both juice and water.
To understand the sense in which it is being used, context matters, but that is only for the language use of ‘or.’
In mathematics, we generally use ‘or’ inclusively. We want to eliminate any uncertainties. So, we define the usage.
In set theory, ‘or’ represents the union of sets when used in an inclusive sense. We say that the union of two sets means elements either in A OR in B.
But is there any way to use the word ‘or’ exclusively in mathematics? Can we have a set that contains elements from one set OR the other, where OR is used in the exclusive sense?
Apparently, yes, and this is the foundation of the symmetric difference operation. The only concept in mathematics where we use ‘or’ in the exclusive sense is the symmetric difference. As discussed before, the symmetric difference is the elements present in A or B but not in A and B.
Definition of Symmetric Difference:
Like any other operation, a symmetric difference also happens between two sets. Suppose we have two sets, A and B. Their symmetric difference would consist of all the elements present in either A or B but not in the intersection of A and B.
‘Symmetric difference between any two sets is defined as a new set containing all the elements present in either of the sets but not in their intersection.’
Let’s solve some examples to comprehend this better.
Example 1
You are given two sets defined as:
A = {2, 6, 7, 9}
B = {2, 4, 6, 10}
Find out the symmetric difference based on the definition provided above.
Solution:
From the definition provided above, we know that symmetric difference is a set containing elements either in A or B but not in both. We look for elements common in A and B. These elements are 2 and 6. A new set would contain all the remaining elements, which are:
{4, 7, 9, 10}
This set represents the symmetric difference of sets A and B.
Representation of Symmetric Difference:
When representing the symmetric difference between any two sets, let us assume set A and B are denoted by the symbol ∆.
Mathematically it is represented using:
A ∆ B = (A U B) – (A ∩ B)
This representation has been repeatedly explained above. It implies that A ∆ B represents a set that contains the elements from the union of two sets, A and B, minus the intersection between them. Symmetric Difference, in other words, is also called disjunctive union.
The symbol ∆ is also a binary operator. Like other binary operators, it takes two operands, two different or identical sets as we know for other operations and their applications for calculating probability between events.
The symmetric difference is not only restricted to set operations. We can also use it to calculate the probability of certain multiple events. We can convert the equation written above to an equation with probability.
From the above equation, we observe three different operations. Before we try to solve any example, let us first revise these operations.
Union of Two Sets:
The union between any two sets such as A and B represents a new set containing all A and B elements.
The intersection of Two Sets:
The intersection between two sets, A and B, represents a new set containing elements common to A and B. In other words, all the elements present in A and B.
The difference between the Two Sets:
The difference between sets such as between A and B with respect to B is a new set containing all the elements present in A but not in B.
Now that we have understood the basic operations that make up the symmetric differences, let’s solve an example.
Example 2
You are given two sets, A and B, which are defined as:
A = {2, 4, 6, 8}
B = {2, 5, 7, 8}
Find out the symmetric difference B ∆ A.
Solution:
Symmetric difference of B with respect to A is defined as:
B ∆ A = (B U A) – (B ∩ A)
(B U A) = {2, 4, 5, 6, 7, 8}
(B ∩ A) = {2, 8}
B ∆ A = (B U A) – (B ∩ A) = {4, 5, 6, 7}
This is the symmetric difference of B with respect to A.
Representation using Other Operations
In the above section, we represented the symmetric difference operation using the union of a set, intersection, and difference between sets. This is shown below:
A ∆ B = (A U B) – (A ∩ B)
Another way to represent them is by using differences and union alone.
A ∆ B = (A – B) U (B – A)
This is an equivalent expression for the symmetric differences. We can define this representation by saying that it is the union of all the elements present in A but not in B with all the B’s elements but not A.
As we can notice from the two different representations, one thing common to both is calculating the difference between the two sets. Not only the difference, we observe that the equations are symmetric as well. By symmetric, we mean we can change the set A and B positions with no effect on the result whatsoever.
The Difference between Sets vs Symmetric Difference
As the name suggests, symmetric difference undergoes some difference operation as well. Then how is it different from only the difference of sets?
To understand this, let us look at the term ‘Symmetric Difference.’ The name ‘symmetric’ suggests that the operation must be symmetric. However, we know for a fact that the difference between sets is not symmetric. The difference of set A with respect to set B will not be the same as set B’s difference with respect to A.
This symmetric nature of symmetric differences sets them apart from the difference between sets.
Venn Diagram Representation
Venn diagrams are the most appropriate tool to understand the data or sets visually. We can use Venn diagrams to understand the set and different operations being performed between different sets. We will be using it to understand the concept at hand. We can understand these operations more comprehensively, but you need to keep in mind that we can only use Venn diagrams to represent finite sets. The region inside the Venn diagram represents the set. We can also represent any shape. Also, note that the points inside this diagram represent the elements of a set. This method of visualization offers a holistic understanding of symmetric differences.
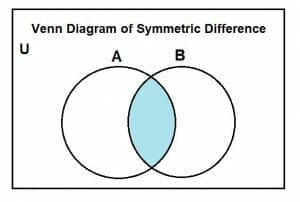
Let us say we have a universal set U. Set A and B are subsets of the universal set. There is also some intersecting region between these sets A and B. The region in blue represents the symmetric difference between set A and B.
If we look at the diagram closely, we can observe that the intersecting region is not a part of the symmetric difference. In comparison, the rest of sets A and B are included in the designated part.
Let’s look at how we can construct this diagram.
Example 3
We have two sets defined as:
A = {2, 4, 6, 7}
B = {2, 4, 8, 10}
Draw the Venn Diagram for the symmetric difference between them.
Solution:
We will be tackling this problem step by step. The first step is to find the union of set A and B, which comes out to be:
A U B = {2, 4, 6, 8, 7, 10}
Once we have calculated the union, the second step is to calculate the intersection of two sets. The intersection of set A and B will be:
A ∩ B = {2, 4}
We take the difference between these two sets in the next step: A U B and A ∩ B.
(A U B) – (A ∩ B) = {6, 8, 7, 10}
We will draw two circles representing set A and B. As 2, 4 are the common elements between them. There must be some intersecting region. After we have listed the intersecting region elements, we list the remaining elements from the respective circles’ symmetric differences.
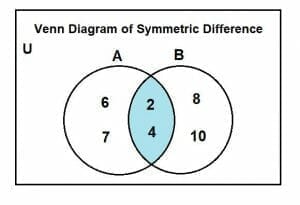
When we look at this diagram, we can see that U is a universal set. Set A and B are the subsets of set U. Elements 2 and 4 are the intersecting elements, so they are marked in the intersecting region. The yellow region is the union of sets except for the intersecting region. This is represented as:
A ∆ B = (A U B) – (A ∩ B)
Properties of Symmetric Difference
Commutativity Property:
Any operation is considered commutative in the mathematical domain if you change the operands’ order, but this change does not affect the result. It is one of the most basic properties of several binary operations.
The commutative property of symmetric difference states that:
‘The symmetric difference of A with respect B is equal to the symmetric difference of B with respect to A.’
So, if we have two sets, A and B, mathematically, we can write that:
A ∆ B = B ∆ A
Let’s solve an example to comprehend this.
Example 4
You are given two sets, A and B:
A = {5, 6, 7, 10}
B = {10, 2, 4, 7}
Prove that symmetric difference is commutative using these sets.
Solution:
We are given that A ∆ B = B ∆ A, so we divide the equation into the left and right-hand sides. First solving for the left-hand side. We know that:
A ∆ B = (A U B) – (A ∩ B)
(A U B) = {5, 6, 7, 10, 2, 4}
(A ∩ B) = {7, 10}
A ∆ B = (A U B) – (A ∩ B) = {5, 6, 2, 4}
Now solving for the right-hand side:
B ∆ A = (B U A) – (B ∩ A)
(B U A) = {5, 6, 7, 10, 2, 4}
(B ∩ A) = {7, 10}
B ∆ A = (B U A) – (B ∩ A) = {5, 6, 2, 4}
As we can see, both the right and left-hand sides are equal. So, the commutative property holds.
Associativity Property:
Associativity means that you can shift or reposition the parentheses without worrying about changes in the equation’s results.
However, the associative law of symmetric difference states that changing parentheses’ position in any expression of sets involving symmetric difference operation will not affect the results in any manner whatsoever.
The grouping of sets for symmetric differences will not affect the result.
So, if we have three sets, namely A, B, and C. Associativity property of symmetric difference can be mathematically written as:
(A ∆ B) ∆ C = A ∆ (B ∆ C)
The following example will help us understand this better.
Example 4
You are given three sets A, B, and C:
A = {5, 6, 7, 10}
B = {10, 2, 4, 7}
C = {7, 8, 9, 10}
Prove that symmetric difference is associative using these sets.
Solution:
We are given that (A ∆ B) ∆ C = A ∆ (B ∆ C) to divide the equation into left and right-hand sides. First solving for the left-hand side. We know that:
A ∆ B = (A U B) – (A ∩ B)
(A U B) = {5, 6, 7, 10, 2, 4}
(A ∩ B) = {7, 10}
A ∆ B = (A U B) – (A ∩ B) = {5, 6, 2, 4}
(A ∆ B) ∆ C = {2, 4, 5, 6, 7, 8, 9, 10}
Now solving for the right-hand side:
B ∆ C = (B U C) – (B ∩ C)
(B U C) = {2, 4, 7, 8, 9, 10}
(B ∩ C) = {7, 10}
B ∆ C = (B U C) – (B ∩ C) = {2, 4, 8, 9}
A ∆ (B ∆ C) = {2, 4, 5, 6, 7, 8, 9, 10}
As we can see, both the right and left-hand sides are equal. So, the associative property holds.
Idempotent property:
This property states that the symmetric difference of a set with itself will give the null set. Mathematically, it can be written as:
A ∆ A = Ⲫ
Property of Ⲫ:
The null set’s property states that any set’s symmetric difference with the null set will result in the set itself. Mathematically, this property can be stated as:
A ∆ Ⲫ = A
To further strengthen the concept of the symmetric difference, consider the following practice problems.
Practice Problems
- If C = {x< 7; x in N} and B = {2, 3, 4, 5, 9}. Find out C ∆ B.
- You are given A = {4, 3, 8, 9} and A ∆ B = {3, 10}. Find out the elements of set B.
- If A = {1, 6, 8, 9, 10} and B = {5, 7, 8, 9, 10, 11, 12}. Label and draw A ∆ B on Venn diagram.
- Prove that the idempotent property with respect to SD holds for set A = {4 < x<= 10, x in N}
- You are given A = {10, 15, 17, 1} and B = {15, 16, 17, 18}. Find out the difference and symmetric difference between them.
Answers
- {6, 9}
- B = {4, 8, 9, 10}
- Left for the reader
- Left for the reader
- Difference = {1, 10}, Symmetric difference = {1, 10, 16, 18}
