The Symmetric Property of Equality – Explanation and Examples

The symmetric property of equality states that it does not matter whether a term is on the right or left side of the equal sign.

This property essentially states that flipping the left and right sides of an equation does not change anything. This fact is useful in arithmetic, algebra, and computer science.

Before reading on, make sure to review the properties of equality.

This section covers:

• What Is Symmetric Property of Equality
• Symmetric Property of Equality Definition
• Example of Symmetric Property of Equality

What Is Symmetric Property of Equality

The symmetric property of equality basically states that both sides of an equation are the same. This makes sense because when something is symmetric, it is the same on both sides.

The symmetric property of equality allows the left side of an equation to become the right-side and vice versa. It establishes equality as an equivalence relation in math.

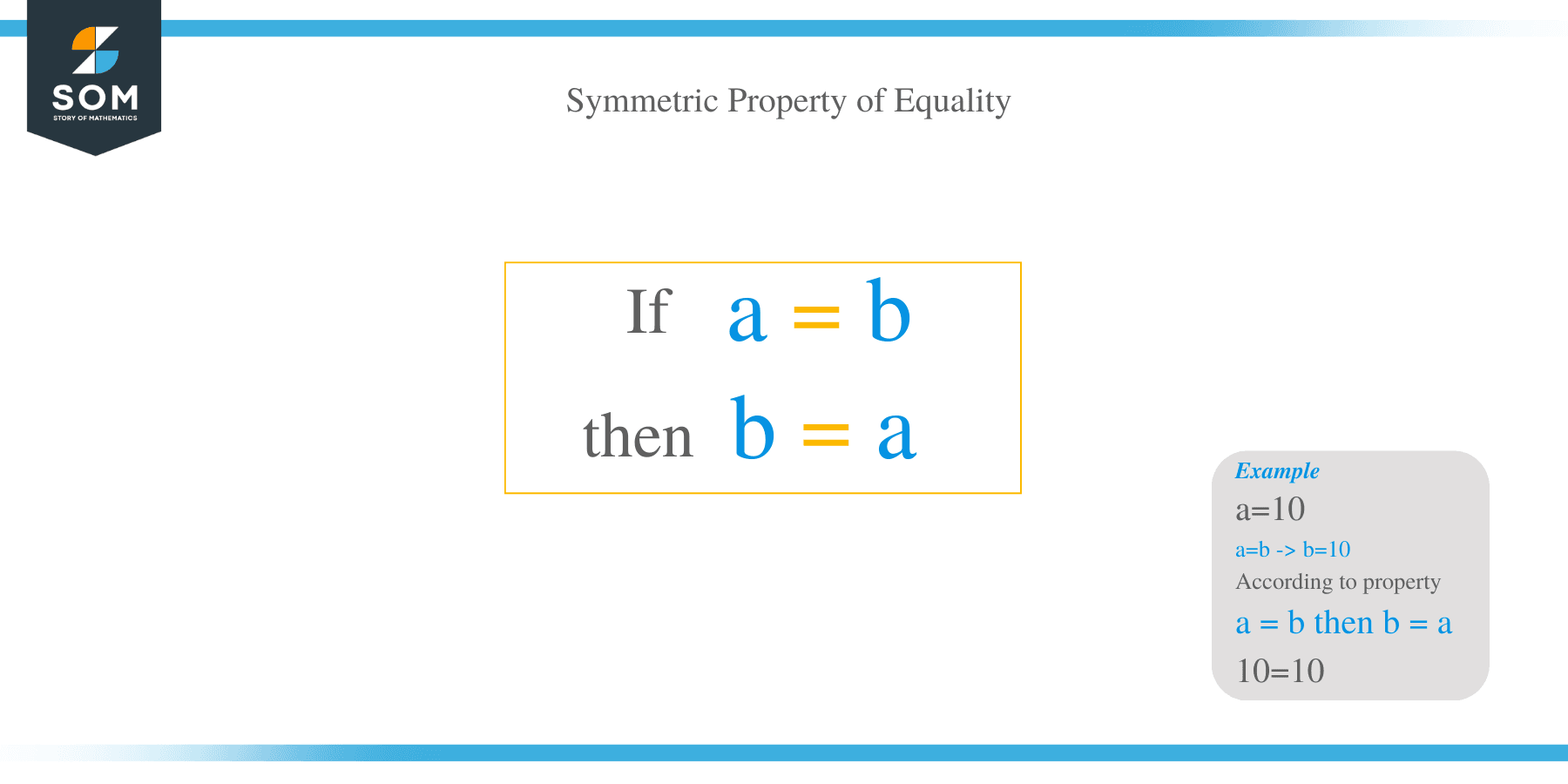
Equivalence Relationships

An equivalence relation is a math relationship that is reflexive, symmetric, and transitive. That is, if two things are related by an equivalence relationship, then:

• The things have an equivalence relationship with themselves.
• The order of the equivalence relationship does not matter.
• If two things both have an equivalence relationship with a third thing, then they have an equivalence relationship with each other.

Given the term “equivalence relation,” it makes sense that equality is an equivalence relation. However, it is not the only one. Similarity and congruence in triangles are equivalence relationships.

Even if the symmetric property of equality seems obvious, there are other relationships that do not work this way. For example, it matters whether a term is to the right or the left of a greater than sign.

Symmetric Property of Equality Definition

The symmetric property of equality states that if a first term is equal to a second, then the second is equal to the first.

Essentially, the property says that it doesn’t matter which term is on the left side of an equal sign and which term is on the right.

Arithmetically, let $a$ and $b$ be real numbers such that $a=b$. The symmetric property of equality states that:

$b=a$

Converse

The converse of the symmetric property of equality is also true. That is, if $a$ and $b$ are real numbers such that $a\neq b$, then $b\neq a$.

Is the Symmetric Property of Equality an Axiom?

Euclid did not give the symmetric property of equality a name, but he did use it. This may be because the symmetric property of equality seemed so fundamental as not worth mentioning.

Giuseppe Peano made a list of axioms in the 1800s, when the study of arithmetic was becoming more formal. His list did include the symmetric property of equality. This is likely because symmetry, reflexivity, and transitivity are necessary to establish an equivalence relation.

The symmetric property, however, can be derived from the substitution and reflexive properties of equality. Example 3 does just that.

Example of Symmetric Property of Equality

Symmetry may seem so obvious as to be unimportant. Yet, everyday language illustrates an important situation where the symmetric property of equality does not apply. This highlights that it should not be just taken for granted.

Generally, “is” translates to “=” when converting from speaking to mathematical statements.

One might say that if it is broccoli, then it is green. This, however, does not work the other way. If it is green, it is not broccoli.

In this case, broccoli $\neq$ green. Instead, broccoli $\Rightarrow$ green. This is read as “broccoli implies green.”

Thus, symmetry should not be taken for granted. Implications and comparisons (greater than, lesser than) are all examples of relations that only work in one direction.

Examples

This section covers common problems using the symmetric property of equality and their step-by-step solutions.

Example 1

Let $a, b, c$ and $d$ be real numbers such that $a=b$ and $c=d$. Which of the following are true?

A. $b=a$
B. $d=c$
C. $bc=ac$

Solution

The first two statements by he symmetric property. The third one is true from a both the symmetric and multiplication properties.

The symmetric property states that if $a=b$, then $b=a$. Likewise, if $c=d$, then $d=c$.

If $a=b$ and $c$ is a real number, then $ac=bc$. This is true according to the multiplication property of equality. Then the symmetric property states that $bc=ac$ too.

Example 2

The distance from Earth to Mars is 232.54 million miles. What is the distance from Mars to Earth? Which properties of equality justify this?

Solution

The distance from Earth to Mars is 232.54 million miles. According to the symmetric property of equality, the distance from Mars to Earth is the same. It will also be 232.54 million miles.

Why?

The symmetric property of equality states that if $a$ and $b$ are real numbers such that $a=b$, then $b=a$.

The distance from Earth to Mars is equal to the distance from Mars to Earth. Thus, the distance from Mars to Earth is equal to the distance from Earth to Mars.

The transitive property of equality says let $a, b,$ and $c$ be real numbers. If $a=b$ and $b=c$, then $a=c$.

Note that distance from Earth to Mars is 232.54 million miles and the distance from Mars to Earth is equal to the distance from Earth to Mars. Thus, the transitive property of equality states that the distance from Mars to Earth will also be 232.54 million miles.

Example 3

Use the substitution and reflexive properties of equality to derive the symmetric property of equality.

Solution

The substitution property of equality says let $a$ and $b$ be real numbers such that $a=b$. Then $a$ can replace $b$ in any equation. The reflexive property of equality states that for any real number $a$, $a=a$.

$a=b$ is given. The reflexive property of equality states that $b=b$.

The substitution property then states that $a$ can replace $b$ in any equation. Thus, since $b=b$, $b=a$.

But, this is the symmetric property of equality. Thus, the symmetric property of equality is deducible from the substitution and reflexive properties.

Example 4

The addition property of equality says let $a, b,$ and $c$ be real numbers such that $a=b$. Then $a+c=b+c$. Use the symmetric property of equality to find an equivalent formulation of this property.

Solution

Recall that the symmetric property of equality says that if $a$ and $b$ are real numbers and $a=b$, then $b=a$.

The last part of the addition property of equality states that $a+c=b+c$. Recall that the symmetric property of equality permits swapping the left and right sides of the equation. Thus, if $a+c=b+c$, then $b+c=a+c$.

Thus, another phrasing is let $a, b,$ and $c$ be real numbers such that $a=b$. Then $b+c=a+c$.

Example 5

Let $x$ be a real number such that $7=x$. Use the symmetric and substitution properties of equality to prove that $35=5x$.

Solution

It is given that $7=x$. According to the substitution property of equality, $7$ can replace $x$ in any equation.

But, according to the symmetric property of equality, if $7=x$, then $x=7$. Combining this fact with the substitution property means that $x$ can also replace $7$ in any equation.

It is known that $5\times7=35$. Symmetrically, $35=5\times7$. Since $x$ can replace $7$ in any equation, $35$ is also equal to $5\times x$.

Thus, $35=5x$ as required.