Tangent to a Circle – Explanation & Examples

Have you ever done or saw fencing around the garden or some road due to law and order situation? The police will not allow you to get close to the fence. Some might get a chance to touch the fence and walk away. If they walk in a straight line, they are basically following a tangent path for the shape made inside the fencing.

That is a definition of a tangent that is a line that touches the shape at any one point and moves away. And that is what the Latin word “tangent” means, “to touch.”

Tangents can be formed around any shape, but this lesson will focus on the tangents to a circle.

In this article, you will learn:

• What the tangent of a circle is; &
• How to find the tangent of a circle.

What is the Tangent to a Circle?

The tangent to a circle is defined as a straight line that touches the circle at a single point. The point where the tangent touches a circle is known as the point of tangency or the point of contact.

On the other hand, a secant is an extended chord or a straight line that crosses a circle at two distinct points.

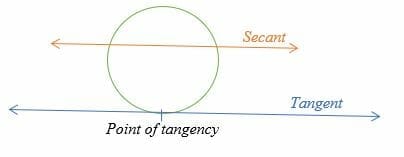
Tangent to a Circle Theorem

The tangent theorem states that a line is a tangent to a circle if and only if the line is perpendicular to the radius drawn to the point of tangency.

Properties of a tangent

• One tangent can touch a circle at only one point of the circle.
• A tangent never crosses a circle, which means it cannot pass through the circle.
• A tangent never intersects the circle at two points.
• The tangent line is perpendicular to the radius of a circle.

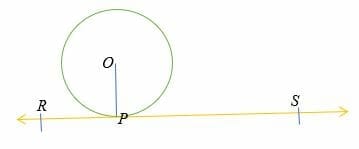
The radius of the circle OP is perpendicular to the tangent line RS.

• The length of two tangents from a common external point to a circle is equal.

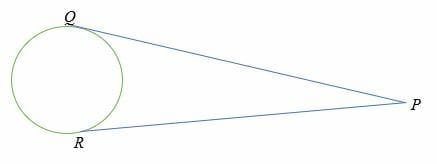
Length PR = Length PQ

How to Find the Tangent of a Circle?

Consider the circle below.

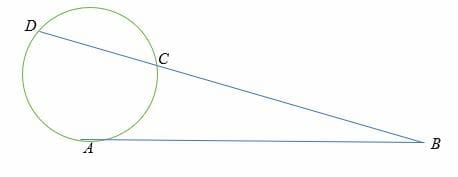
Suppose line DB is the secant and AB is the tangent of the circle, then the of the secant and the tangent are related as follows:

DB/AB = AB/CB

Cross multiplying the equation gives.

AB² = DB * CB ………… This gives the formula for the tangent.

Let’s work out a few example problems involving the tangent of a circle.

Can the two circles be tangent?

Yes!

The two circles are tangent if they are touching each other at exactly one point. According to the definition of a tangent, it is that touches the circle at exactly one point.

The following diagram is an example of two tangent circles.

Example 1

Find the length of the tangent in the circle shown below.

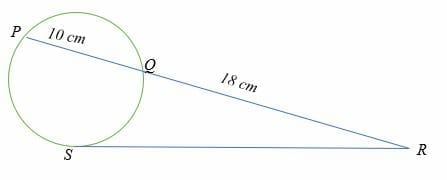
Solution

The above diagram has one tangent and one secant.

Given us the following lengths:

PQ = 10 cm and QR = 18 cm,

Therefore, PR = PQ + QR = (10 + 18) cm

= 28 cm.

⇒ SR² = PR * RQ

⇒ SR² = 28 * 18

⇒ SR² = 504 cm

⇒ √SR² = √504

⇒ SR = 22.4 cm

So, the length of the tangent is 22.4 cm.

Example 2

Find the tangent length in the following diagram, given that AC = 6 m and CB = 10 m.

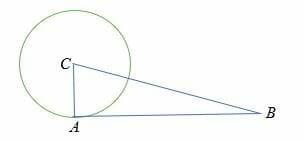
Solution

Since the radius of a circle is perpendicular to the tangent, triangle ABC is a right triangle (angle A = 90 degrees).

By Pythagorean theorem

⇒ AB² + AC² = CB²

⇒ AB² + 6² = 10²

⇒ AB² + 36 = 100

Subtract 36 on both sides.

⇒ AB² = 100 – 36

⇒ AB² = 64

√AB² = √64

AB = 8.

Therefore, the length of the tangent is 8 meters.

Example 3

If DC = 20 inch and BC = 12 inch, calculate the radius shown below.

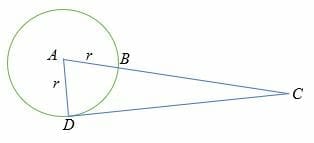
Solution

DC² = AC * BC

But AC = AB + BC = r + 12

20² = 12 (r + 12)

400 = 12r +144

Subtract 144 on both sides.

256 = 12r

Divide both sides by 12 to get

r = 21.3

So, the radius of the circle is 21.3 inches.

Example 4

Determine the value of x in the shown below

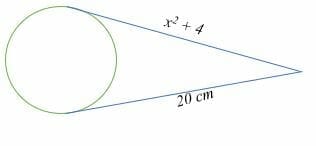
Solution

The length of two tangents from a common external point to a circle is equal. Therefore,

20 = x² + 4

Subtract 4 on both sides.

16 = x²

√16 = √x²

x = 8

Thus, the value of x is 8 cm.

Example 5

Calculate the length of the tangent in the circle shown below.

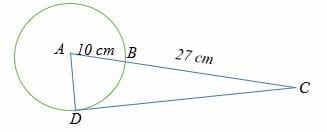
Solution

DC² = 27 (10 + 27)

= 27 *37

DC² = 999

Ignoring the negative value, we have

DC = 31.61

Therefore, the of the tangent is 31.61 cm

Example 6

Find the length of line XY in the diagram below.

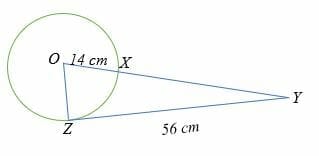
Solution

Let XY = x

x (x +14) = 56²

x² + 14x = 3136

x² + 14x – 3136 = 0

Solve the quadratic equation to get,

x = 63.4

Therefore, the length of XY is 63.4 cm.

Example 7

Calculate the length of AB in the circle below.

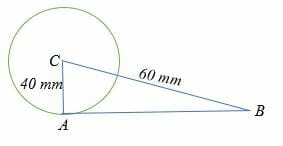
Solution

By Pythagorean theorem,

40² + AB²= 100²

`1600 + AB² = 10000

AB² = 8400

AB = 91.7

Hence, the length of AB is 91.7 mm