
- the function that assigns to each pair of positive integers the first integer of the pair.
- the function that assigns to each positive integer the largest decimal digit.
- the function that assigns to a bit string the number of ones minus the number of zeros in that string.
- the function that assigns to each positive integer the largest integer that does not exceed the square root of the integer.
- the function that assigns to a bit string the longest string of ones in that string.
This question aims to find the domain and range of the given functions.
A function is a relationship between a set of inputs and a set of permitted outputs. In a function, each input is related to precisely one output.
A domain takes a set of possible values for the components of a function. Suppose $f(x)$ is a function, the set of $x$ values in $f(x)$ is called domain of $f(x)$. In other words, we can define domain as the whole set of possible values for independent variables.
A range of the function is a set of values that the function can take. It is a set of values that the function returns after we enter an $x$ value.
Expert Answer
- We have the function that assigns to each pair of positive integers, the first integer of the pair.
The positive integer is a natural number, and the only non-positive natural number is zero. This implies that $N-\{0\}$ refers to a set of positive integers under consideration. So its domain will be:
Domain $=\{(x,y)|x=1,2,3,\cdots\,\,\text{and}\,\, y=1,2,3,\cdots\}$
$=\{(x,y)|x\in N-\{0\}\wedge x\in N-\{0\}\}$
$=(N-\{0\})\times (N-\{0\})$
And range will be a positive first integer of the domain, that is:
Range $=\{1,2,3,\cdots\}=N-\{0\}$
- We have a function that assigns to each positive integer its largest decimal digit.
In this case, a domain will be a set of all positive integers:
Domain $=\{1,2,3,\cdots\}=N-\{0\}$
And the range will be a set of all the digits from $1$ to $9$, that is:
Range $=\{1,2,3,4,5,6,7,8,9\}$
- We have a function that assigns to a bit string the number of ones minus the number of zeros in the string.
The domain of such a function will be a set of all bit rings:
Domain $=\{\lambda,0,1,00,01,11,10,010,011,\cdots\}$
And according to the statement, the range may take on positive and negative values and a zero, since it will be a set of all differences between the number of ones and number of zeros in a string. Therefore:
Range $=\{\cdots,-2,-1,0,1,2,3,\cdots\}$
- We have the function that assigns to each positive integer the largest integer not exceeding the square root of the integer.
Here, the domain will be a set of all positive integers:
Domain $=\{1,2,3,\cdots\}=N-\{0\}$
The range is defined as the set of the largest integer that does not exceed the square root of a positive integer. We can see that the set contains all positive integers, so:
Range $=\{1,2,3,\cdots\}=N-\{0\}$
- Lastly, we have the function that assigns to a bit string the longest string of ones in the string.
The domain of such a function will be a set of all bit rings:
Domain $=\{\lambda,0,1,00,01,11,10,010,011,\cdots\}$
The range will be a set of all longest strings of ones in any string. As a result, the range only contains strings that contain the digit $1$:
Range $=\{\lambda,1,11,111,1111,11111,\cdots\}$
Example
Find the domain and range of the function $f(x)=-x^2-4x+3$.
Since $f(x)$ has neither undefined points nor domain constraints, therefore:
Domain: $(-\infty,\infty)$
And $f(x)=-x^2-4x+3=-(x+2)^2+7$
Since, $-(x+2)^2\leq 0$ for all real $x$.
$\implies -(x+2)^2+7\leq 7$
Hence, the range is: $(-\infty,7]$
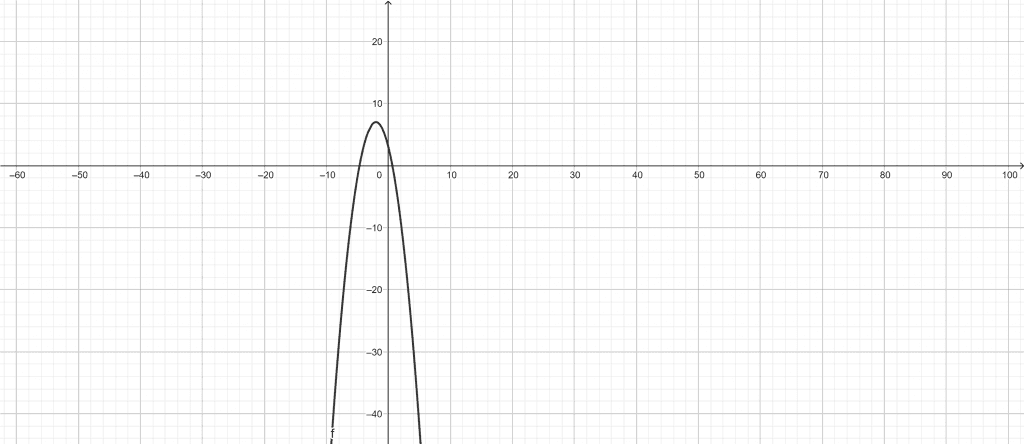
Graph of $f(x)$
Images/mathematical drawings are created with GeoGebra.
