A marble moves along the x-axis. The potential-energy function is shown in the figure (figure 1) .

• At which of the labeled $x-$coordinates is the force on the marble zero?
• Which of the labeled $x-$coordinates is a position of stable equilibrium?
• Which of the labeled $x-$coordinates is a position of unstable equilibrium?

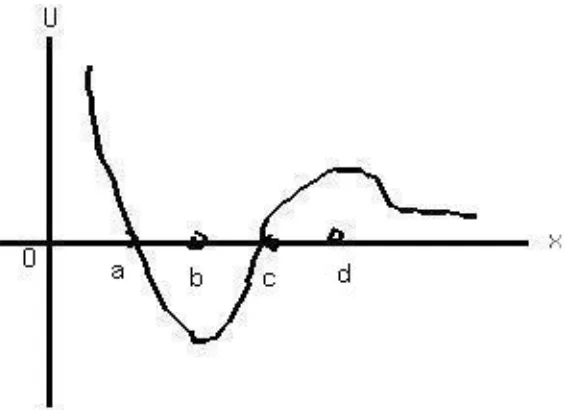
The objective of this question is to identify the points at which the force on the marble is zero and the points of stable and unstable equilibrium. 

Force is defined as an action that tends to maintain or change the movement of an object. It is a vector quantity that has both magnitude and direction.

Potential energy is the energy that results from a change in position or configuration.

Equilibrium is a state of balance. When two opposing forces balance each other on an object under consideration, it is said to be in a state of equilibrium. When displaced from equilibrium or when the body is in its minimum energy condition, a system is said to be in stable equilibrium. It experiences a net force or torque in the opposite direction of displacement.

In other words, if a body tends to return to its equilibrium position, this implies that it is in a stable equilibrium zone, and the force that compelled it back is a restoring force. When an equilibrium system is displaced and the resulting net force pushes the object further away from the equilibrium position, the system is said to be in unstable equilibrium.

Expert Answer

• The force is zero at the points $B$ and $D$, since at these points the slope of the graph is zero.
• Point $B$ is in stable equilibrium because moving the marble away from point $B$ would require energy.
• Point $D$ is in an unstable equilibrium because moving the marble away from point $D$ decreases the potential energy, which causes the kinetic energy to increase, making it unstable.

Example 1

A $40$ N block is lifted $8$ m vertically upward. Determine the amount of potential energy it contains.

Solution

Let $W$ be the weight of the block, then:

$W=40$ N

Let $h$ be its height, then:

$h=8$ m

Since, Potential Energy (P.E) $=mgh=wh$

Thus, P.E $=(40)(8)=320$ J

Example 2

Work out the force exerted by labor while pulling a $70$ kg trolley at a rate of $2.1$ m/s$^2$.

Solution

Let $m$ be the mass of the trolley, then:

$m=70$ kg

Let $a$ be the acceleration, then:

$a=2.1$ m/s$^2$

Let $F$ be the force exerted by labor on the trolley, then by Newton’s second law of motion:

$F=ma$

$F=(70)(2.1)=147$ N

Previous Question < > Next Question