Trigonometry

Triangles may seem like simple figures, but the mathematics behind them is deep enough to be considered its own subject: trigonometry.

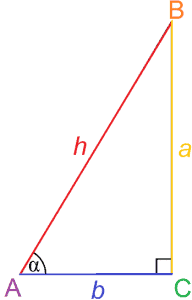
As the name suggests, trigonometry is the study of triangles. More specifically, trigonometry deals with the relationships between angles and sides in triangles.

Somewhat surprisingly, the trigonometric ratios can also provide a richer understanding of circles. These ratios are often used in calculus as well as many branches of science including physics, engineering, and astronomy.

The resources in this guide cover the basics of trigonometry, including a definition of trigonometric ratios and functions. They then go over how to use these functions in problems and how to graph them.

Finally, this resource guide concludes with an explanation of the most common trigonometric identities.

Basic Trigonometry

Trigonometry especially deals with the ratios of sides in a right triangle, which can be used to determine the measure of an angle. These ratios are called trigonometric functions, and the most basic ones are sine and cosine.

These two functions are used to define the other well-known trigonometric functions: tangent, secant, cosecant, and cotangent.

This section begins by reviewing right triangles and explaining the basic trigonometric functions. It also explains their reciprocals. The topic also covers how to evaluate trigonometric angles, especially the special angles of 30-, 45-, and 60-degrees.

Finally, the guide to this topic covers how to deal with the inverses of trigonometric functions and the two most common ways to measure angles.

• Identify the Sides of Right Triangles
• Trigonometric Functions or Trig. Ratios
• Sine
• Cosine
• Tangent
• Review of Sine, Cosine, and Tangent
• Secant, Cosecant, Cotangent
• Sin, Cos, Tan, Sec, Csc, Cot
• Co-Functions
• Evaluate Trigonometric Angles
• Special Angles: 30-Degrees, 45-Degrees, 60-Degrees
• Using a Calculator
• Inverse Trigonometry
• Degrees and Radians

Applications of Trigonometry

There are actually a wide variety of theoretical and practical applications for trigonometric functions. They can be used to find missing sides or angles in a triangle, but they can also be used to find the length of support beams for a bridge or the height of a tall object based on a shadow.

This topic covers different types of trigonometry problems and how the basic trigonometric functions can be used to find unknown side lengths. It also covers how they can be used to find angles and even the area of a triangle.

Finally, this section concludes with subtopics on the Laws of Sines and the Law of Cosines.

• Trigonometry Problems
• Sine Problems
• Cosine Problems
• Tangent Problems
• Find Unknown Sides of Right Angles
• Find Height of Object Using Trigonometry
• Trigonometry Applications
• Angle of Elevation and Depression
• Area of Triangle Using the Sine Function
• Law of Sines or Sine Rule
• Law of Cosines or Cosine Rule

Trigonometry in the Cartesian Plane

Trigonometry in the Cartesian Plane is centered around the unit circle. That is, the circle centered at the point (0, 0) with a radius of 1. Any line connecting the origin with a point on the circle can be constructed as a right triangle with a hypotenuse of length 1. The lengths of the legs of the triangle provide insight into the trigonometric functions. The cyclic nature of the unit circle also reveals patterns in the functions that are useful for graphing.

This topic begins with a description of angles at the standard position and coterminal angles before explaining the unit circle and reference angles. It then covers how the values of the trigonometric functions change based on the quadrant of the Cartesian Plane. Finally, this section ends by explaining how the unit circle and the xy-plane can be used to solve trigonometry problems.

• Angles at Standard Position and Coterminal Angles
• Unit Circle
• Reference Angle
• Trigonometric Ratios in the Four Quadrants
• Finding the Quadrant in Which an Angle Lies
• Coterminal Angles
• Trigonometric Functions in the Cartesian Plane
• Degrees and Radians
• Evaluating Trigonometric Functions for an Angles, Given a Point on the Angle
• Evaluating Trigonometric Functions Using the Reference Angle
• Finding Trigonometric Values Given One Trigonometric Value/Other Info
• Evaluating Trigonometric Functions at Important Angles

Graphs of Trigonometric Functions

Although the unit circle in the Cartesian plane provides into trigonometric functions, each of these functions also has its own graph. These graphs are cyclic in nature. Typically, graphs of trig functions make the most sense when the x-axis is divided into intervals of pi radians while the y-axis is still divided into intervals of whole numbers.

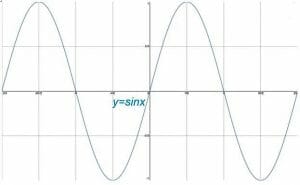
This topic covers the basic graphs of sine, cosine, and tangent. It then discusses transformations of those graphs and their properties. Finally, the topic concludes with a subtopic about the graphs of the reciprocals of the basic trig functions.

• Trigonometry Graphs
• Sine Graph
• Cosine Graph
• Tangent Graph
• Transformations of Trigonometric Graphs
• Graphing Sine and Cosine with Different Coefficients
• Maximum and Minimum Values of Sine and Cosine Functions
• Graphing Trig Functions: Amplitude, Period, Vertical, and Horizontal Shifts
• Tangent, Cotangent, Secant, Cosecant Graphs

Trigonometric Identities

This is the point where trigonometric functions take on a life of their own apart from their basis in triangle side ratios. The functions contain numerous identities that illuminate the relationship between different types of trig functions.

These identities can be used to find the values of angles outside the common reference angles. In fact, they were the main tool available for doing that before calculators.

This topic explains trigonometric identities and how to find and remember them. It also explains how to use the identities to simplify expressions, which involves a fair amount of algebraic manipulation.

The guide goes on to explain how to find the values of different angles based on reference angles with the sum and difference identities and the double-angle and half-angle formulas. The topic continues and concludes with more ways to simplify, factor, and solve trigonometric equations.

• Trigonometric Identities
• Trigonometric Identities: How to Derive/ Remember Them
• Using Trigonometric Identities to Simplify Expressions
• Sum and Difference Identities
• Double-Angle and Half-Angle Formulas
• Trigonometric Equations
• Simplifying Trigonometric Expressions Using Trig Identities
• Simplifying Trigonometric Expressions Involving Fractions
• Simplifying Products of Binomials Involving Trigonometric Functions
• Factoring and Simplifying Trigonometric Expressions
• Solving Trigonometric Equations
• Solving Trigonometric Equations Using Factoring
• Examples with Trigonometric Functions: Even, Odd, or Neither
• Proving a Trigonometric Identity