This problem aims to build our understanding of random events and their predictable outputs. The concepts behind this problem are primarily associated with a probability and probability distribution.
We can define probability as a way to indicate the occurrence of an unanticipated event, and the probability can be between zero and one. It estimates the possibility of an event, such events that are difficult to forecast an output. Its standard description is that a likelihood of an event occurring is equal to the ratio of fair outcomes and the total number of trials.
Given as:
\[P(\text{Event to occur})=\dfrac{\text{Favourable Events}}{\text{Total Events}}\]
Expert Answer
As per the given statement, we have $8$ white, $4$ black, and $2$ orange balls. Each selection of a randomly chosen ball results in a win or a loose denoted b $(X)$. The possible results of the experiment are:
\[\{WW\},\space \{WO\},\space \{OO\},\space \{WB\},\space \{BO\},\space \{BB\}\]
The values of $(X)$ corresponding to the outcomes of the events listed are:
\[\{WW=-2\},\space \{WO=-1\},\space \{OO=0\},\space \{WB=1\},\space \{BO=2\},\space \{BB=4\}\]
Where $W$ stand for White, $O$ for orange, and $B$ stands for the black ball.
We are to choose $2$ balls at random from a total of $8+4+2 = 14$ balls, so the combination becomes:
\[C^{n}_{r}=\dfrac{n!}{r!(n-r)!}\]
\[C^{14}_{2}=\dfrac{14!}{2!(14-2)!}\]
\[C^{14}_{2}=\dfrac{14!}{2!\cdot 12!}\]
\[C^{14}_{2}=91\]
The probability of choosing two white balls is:
\[P(X = -2)=P(\{W, W\})=\dfrac{\begin{pmatrix} 8 \\ 2 \end{pmatrix}}{\begin{pmatrix} 14 \\ 2 \end{pmatrix}}=\dfrac{28}{91} \]
Similarly, the rest of the probabilities can be calculated as follows:
\[P(X = -1)=P(\{W, O\})=\dfrac{\begin{pmatrix} 8 \\ 1 \end{pmatrix} \begin{pmatrix} 2 \\ 1 \end{pmatrix}}{\begin{pmatrix} 14 \\ 2 \end{pmatrix}} = \dfrac{16}{91} \]
\[P(X = 1)=P(\{W, B\})=\dfrac{\begin{pmatrix} 8 \\ 1 \end{pmatrix} \begin{pmatrix} 4 \\ 1 \end{pmatrix}}{\begin{pmatrix} 14 \\ 2 \end{pmatrix}}=\dfrac{32}{91} \]
\[P(X = 0)=P(\{O, O\})=\dfrac{\begin{pmatrix} 2 \\ 2 \end{pmatrix}}{\begin{pmatrix} 14 \\ 2 \end{pmatrix}}=\dfrac{1}{91} \]
\[P(X = 2)=P(\{O, B\})=\dfrac{\begin{pmatrix} 2 \\ 1 \end{pmatrix} \begin{pmatrix} 4 \\ 1 \end{pmatrix}}{\begin{pmatrix} 14 \\ 2 \end{pmatrix}}=\dfrac{8}{91} \]
\[P(X = 4)=P(\{B, B\}) = \dfrac{\begin{pmatrix} 4 \\ 2 \end{pmatrix}}{\begin{pmatrix} 14 \\ 2 \end{pmatrix}}=\dfrac{6}{91} \]
Since we have the probability distribution, we are going to use the formula $\mu = \sum x_{\iota} P(X=x_{\iota})$ to find the expected value of $X$:
\[\mu=-2\cdot\dfrac{28}{91}-1\cdot\dfrac{16}{91}+0\cdot\dfrac{1}{91}+1\cdot \dfrac{32}{91}+2\cdot\dfrac{8}{91}+4\cdot\dfrac{6}{91}\]
\[\mu=0\]
Numerical Result
The probabilities associated with each value of $X$ are given in the table:
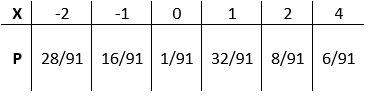
Figure-1
Example
A claim suffered that $60\%$ of all solar systems installed, the utility bill is decreased by at most one-third. Therefore, what could be the probability that the utility bill will be lowered by at minimum one-third in at least four out of the five inductions?
Assume $X$ be equal to measuring the number of reduced utility bills by at least one-third in five solar systems installations, with some certain parameters $n = 5$, $p = 0.6$ and $q = 1− p = 0.4$. We are requested to find the subsequent probabilities:
Part a:
\[P(X=4)=\begin{pmatrix} 5 \\4\end{pmatrix} (0.6)^4(0.4)^{5−4} = 0.259 \]
Part b:
\[P(X\geq 4)=P(X = 4) + P(X = 5) = 0.259+\begin{pmatrix} 5 \\ 5 \end{pmatrix}(0.6)^5 (0.4)^{5−5} = 0.259 + 0.078 = 0.337\]
Image/Mathematical drawings are created in Geogebra.