- Home
- >
- Vector equations – Explanation and Examples
JUMP TO TOPIC
Vector Equations – Explanation and Examples
 In vector geometry, one of the most important concepts in solving real-world problems is using vector equations. The vector equation is defined as:
In vector geometry, one of the most important concepts in solving real-world problems is using vector equations. The vector equation is defined as:
“The vector equation is an equation of vectors which is when solved, gives the result in the form of a vector.”
In this topic, we shall briefly discuss the following mentioned concepts:
- What is a vector equation?
- How to solve a vector equation?
- What is a vector equation of a straight line?
- What is a vector equation of a circle?
- Examples
- Problems
What Is A Vector Equation?
A vector equation is an equation involving n numbers of vectors. More formally, it can be defined as an equation involving a linear combination of vectors with possibly unknown coefficients, and upon solving, it gives a vector in return.
Generally, a vector equation is defined as “Any function that takes anyone or more variable and in return gives a vector.”
Any vector equation involving vectors with n number of coordinates is similar to the linear equation system with n number of coordinates involving numbers. For example,
Consider a vector equation,
r <4,5,6> + t<3,4,1> = <8,5,9>
It can also be written as
<4r,5r,6r> + <3t,4t,1t> =<8,5,9>
Or
<4r+3t, 5r+4t, 6r+1t> = <8,5,9>
For two vectors to be equal, all the coordinates must be equal, so it can also be written as a system of linear equations. Such a representation is as follows:
4r+3t = 8
5r+4t = 5
6r+1t = 9
So, the vector equation can be solved by converting it into a system of linear equations. Hence, it simplifies and becomes easier to solve.
In our daily life, vectors play a vital role. Most of the physical quantities used are vector quantities. Vectors have many true applications, including the situations designated by force and velocity. For example, if a car is moving on a road, various forces will be acting on it. Some forces act in the forward direction and some in the backward direction to balance the system. So, all these forces are vector quantities. We use vector equations to find out various physical quantities in 2-D or 3-D, such as velocity, acceleration, momentum, etc.
Vector equations give us a diverse and more geometric way of viewing and solving the linear system of equations.
Overall, we can conclude that the vector equation is:
x1.t1+x2.t2+···+xk.tk = b
where t 1,t 2,…,t k,b are vectors in Rn and x 1,x 2,…,xk are unknown scalars, has the same solution set as the linear system with an augmented matrix of the given equation.
Therefore, the vector equation is given as,
r = r0 +kv
Let’s understand this concept with the help of examples.
Example 1
A car moves with a constant velocity on a straight road initially at time t=2 the position vector of the car is (1,3,5) then after some time at t=4, the car’s position vector is described as (5,6,8). Write down the vector equation of the position of the object. Also, express it in the form of parametric equations.
Solution
Since the vector equation of a straight-line is given as
r = r0 +tv
Since,
r0 = <1,3,5>
r = <5,6,8>
<5,6,8> = <1,3,5> + 4v
<5,6,8> – <1,3,5> = 4v
<4,3,3> = 4v
v = <1,3/4,3/4>
Now, finding vector equation of object’s position
r = r0 +tv
r = <1,3,5> + t<1,3/4,3/4>
where vector r is <x,y,z>
<x,y,z> = <1,3,5> + <1t,3/4t,3/4t>
Expressing in the form of the parametric equation:
As two vectors are only equivalent if their coordinates are equal. So, due to equality, we can write as,
x = 1+t
y = 3+3/4t
z = 5+3/4t
The vector equation of lines identifies the position vector of line with reference to the origin and direction vector and we can find out the dimensions of vectors corresponding to any length. This works for the straight lines and curves.
Note: The position vector is used to describe the position of the vector. It is a straight line having one end fixed and the other attached to the moving vector to specify its position.
Let’s understand this concept with the help of examples.
Example 2
Write down the following equations as vector equations
- x=-2y+7
- 3x=-8y+6
- x=-3/5-8
Solution
Let’s consider equation 1 first:
x = -2y+7
Since the equation given above is an equation of a straight-line:
y = mx+c
Firstly, we will select two points on the given line.
Let’s simplify the equation,
x = -2y+7
let y = 0
x = 7
So, the first point is s (7,0) or OS (7,0)
Now let find out the second point that is halfway through the first point then,
Let x = 14
14 = -2y + 7
-2y = 7
y = -3.5
So, the second point T (14, -3.5) or OT (14, -3.5)
Then,
OS – OT = (7,0) – (14, -3.5)
OS – OT = (-7, 3.5)
So, the vector equation form of the above equation is,
R = <7,0> + k<-7,3.5>
R = <7-7k, 3.5k>
Now, let’s solve equation 2:
3x = -8y+6
Since the equation given above is an equation of a straight-line
y = mx+c
Firstly, we will select two points on the given line.
Let’s simplify the equation,
3x = -8y+6
let y = 0
x = 2
So, the first point is s (2,0) or OS (2,0)
Now let find out the second point that is halfway through the first point then,
Let x = 4
12 = -2y+7
-2y = 12-7
y = -5/2
So, the second point T (4, -5/2) or OT (4, -5/2)
Then,
OS – OT = (2,0) – (4, -5/2)
OS – OT = (-2, 5/2)
So, the vector equation form of the above equation is,
R = <2,0> + k<-2,5/2>
R = <2-2k, 5/2k>
Now, let’s do equation 3:
x = -3/5-8
Since the equation given above is an equation of a straight-line
y = mx+c
Firstly, we will select two points on the given line.
Let’s simplify the equation,
x = -3/5y+8
let y = 0
x = 8
So, the first point is s (8,0) or OS (8,0)
Now let find out the second point that is halfway through the first point then,
Let x=16
16 = -3/5y+8
-3/5y = 16-8
y = -13.33
So, the second point T (16, -13.33) or OT (16, -13.33)
Then,
OS – OT = (8,0) – (16, -13.33)
OS – OT = (-8, 13.33)
So, the vector equation form of the above equation is,
R = <8,0> + k<-8,13.33>
R = <8-8k, 13.33k>
Vector Equation Of A Straight Line
We all are familiar with the equation of the line that is y=mx+c, generally called a slope-intercept form where m is the slope of the line and x and y are the point coordinates or intercepts defined on the x and y axes. However, this form of the equation is not enough to completely explain the line’s geometrical features. That’s why we use a vector equation to describe the position and direction of the line completely.
To find the points on the line, we will use the method of vector addition. We need to find out the position vector and the direction vector. For the position vector, we will add the position vector of the known point on the line to the vector v that lies on the line, as shown in the figure below.
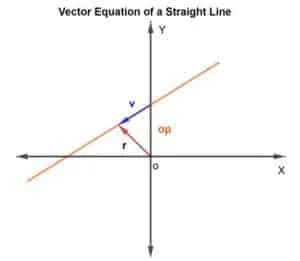
So, the position vector r for any point is given as r = op + v
Then, the vector equation is given as
R = op + kv
Where k is a scalar quantity that belongs from RN, op is the position vector with respect to the origin O, and v is the direction vector. Basically, k tells you how many times you will go the distance from p to q in the specified direction. It can be ½ if half of the distance would be covered and so on.
If two points on the line are known, we can find out the line’s vector equation. Similarly, if we know the position vectors of two points op and oq on a line, we can also determine the vector equation of the line by using the vector subtraction method.
Where,
v = op – oq
Therefore, the equation of vector is given as,
R = op +kv
Let’s solve some examples to comprehend this concept.
Example 3
Write down the vector equation of a line through points P (2,4,3) and Q (5, -2,6).
Solution
Let the position vector of the given points P and Q with respect to the origin is given as OP and OQ, respectively.
OP = (2,4,3) – (0,0,0)
OP = (2,4,3)
OQ = (5, -2,6) – (0,0,0)
OQ = (5, -2 ,6)
Since we know that the vector equation of a line is defined as,
R = OP + kv
Where v = OQ – OP
v = (5, -2,6) – (2,4,3)
v = (3, -6, 3)
So, the vector equation of the straight line is given as,
R = <2,4,3> + k<3, -6,3>
Example 4
Determine the vector equation of the line where k=0.75. If the points given on the line are defined as A (1,7) and B (8,6).
Solution:
k is the scale that can vary from -∞ to +∞. In this case, k is given as 0.75, which is the distance covered on AB in the given direction.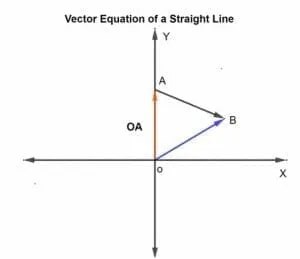
Let the position vector of the given points A and B with respect to the origin are OA and OB, respectively.
OA = (1,7) – (0,0)
OA = (1,7)
OB = (8,6) – (0,0)
OB = (8,6)
Since we know that the vector equation of a line is defined as,
R = OA +kv
Where v = OB – OA
v = (8,6) – (1,7)
v = (7, -1)
So, the vector equation of the straight line is given as,
Where k=0.75
R = <1,7> + 0.75<7, -1>
Example 5
Write down the vector equation of a line through points P (-8,5) and Q (9,3).
Solution
Let the position vector of the given points P and Q with respect to the origin is given as OP and OQ, respectively.
OP = (-8,5) – (0,0)
OP = (-8,5)
OQ = (9,3) – (0,0)
OQ = (9,3)
Since we know that the vector equation of a line is defined as,
R = OP + kv
Where v = OQ – OP
v = (9,3) – (-8,5)
v = (17, -2)
So, the vector equation of the straight line is given as,
R = <-8,5> + k<17, -2>
Vector Equation Of A Circle
Earlier, we have discussed the vector equation of a straight line. Now we will discuss the vector equation of a circle having radius r and with some center c, which we generally say that the circle is centered at c (0,0), but it may be located at any other point in the plane.
The vector equation of a circle is given as
r (t) = <x(t), y(t)>
where x(t) = r.cos(t) and y(t) = r.sin(t), r is the radius of the circle and t is the defined as the angle.
Let us consider a circle with center c and radius r, as shown in the figure below.
.
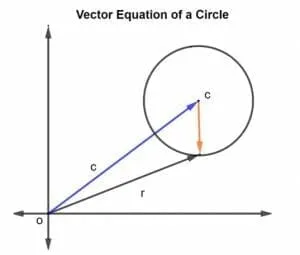
The position vector of the radius and center c is given as r and c, respectively. Then the radius of the circle is represented by vector CR, where CR is given as r – c.
Since the radius is given as r so magnitude if CR can be written as
|CR| = r^2
Or
(r – c). (r – c) = r^2
Or
| r – c| = r
This can also be called a vector equation of a circle.
Example 5
Write down the vector equation and the cartesian equation of a circle with center c at (5,7) and radius 5m.
Solution
Vector equation of a circle:
| r – c| = r
| r – <5,7>| = 5
(r – <5,7>)^2 = 25
Cartesian equation of a circle:
(x-h)^2 +(y-k)^2 = r2
(x-5)^2 + (y-7)^2 = 25
Example 6
Determine if the point (2,5) lies on the circle with the vector equation of a circle given as |r -<-6,2>| = 3.
Solution
We must find out whether the given point lies inside the circle or not provided the circle’s vector equation.
Since putting the value of the point in the given vector equation
= |<2,5>-<-6,2>|
= |<2+6,5-2>|
= |<8,3>|
= √ ((8)^2+(3)^2)
= √ (64+9)
= √ (73) ≠ 3
Hence, the point does not lies inside the circle.
Practice Problems
- Write down the following equations as vector equations : x=3y+5 x=-9/5y+3 x+9y=4
- Determine the equation for the line defined by points A (3,4,5) and B (8,6,7). Find the position vector for a point, half-way between the two points.
- Write a vector equation of the line parallel to vector Q and passing through point o with the given position vector P.
Q = <-2,6> P = <3, -1>
Q = <1,8> P = <9, -3>
- Write down the vector equation of a line through points P (-8/3,5) and Q (5,10).
- A car moves with a constant velocity on a straight road initially at time t=2 the position vector of the car is (1/2,8) then after some time at t=4, the car’s position vector is described as (5,10). Write down the vector equation of the position of the object. Also, express it in the form of parametric equations.
- Write down the vector equation and the cartesian equation of a circle with center c at (8,0) and radius 7m.
- Determine if the point (3,-5) lies on the circle with the vector equation of a circle given as |r -<-3,4>| = 4.
Answers
- (i) . r = <5 – 5k , (-5/3)k (ii) . r = <3 – 3k, (15/9)k > (iii) . r = <4 – 4k, (4/9)k >
- r = <11/2 , 5, 6 >
- (i) . r = <3, -1> + t<-2, 6> (ii) . r = <9, -3> + t<1, 8>
- R = <-8/3, 5> + k<23/3, 5>
- r = <5, 10> +t <-9/8, -1/2> and x = 5 – (9/8)t , y = 10 – (1/2)t
- |r – <8, 0>| = 7 and (x – 8)2 + y2 =49
- NO.
All the vector diagrams are constructed by using GeoGebra.
