
– The radius of the earth is measured to be $6.37\times{10}^6m$. It completes one rotation around its orbit in $24$ hours.
– Part (a) – Calculate the angular speed of the earth.
– Part (b) – If the rotation of the earth is viewed from a location above the north pole, will the angular velocity have a positive notation or negative notation?
– Part (c) – Calculate the speed of a point on the equator of the earth.
– Part (d) – If a point lies halfway between the north pole and equator of the earth, calculate its speed.
The aim of this question is to find the angular speed of the earth, its direction, and the speed of a point lying at certain locations on the earth.
The basic concept behind this article is the Angular Speed or Angular Velocity depending upon the radius of rotation and its relationship with linear velocity.
For any object moving in a circle or around its orbit, its Angular Speed $\omega$ is expressed as follows:
\[\omega=\frac{2\pi}{T}\]
Where:
$T=$ Time period taken to complete one full rotation around the axis.
The Linear speed of an object moving in circular motion is represented as follows:
\[v=r\omega\]
Where:
$r=$ Distance between the axis of rotation and the point at which speed is to be measured.
Expert Answer
Given that:
The Radius of Earth $R=6.37\times{10}^6m$
Time Period of Rotation $T=24h$
\[T=24\times60\times60\ sec\]
\[T=86400s\]
Part (a)
Angular Speed $\omega$ is expressed as follows:
\[\omega=\frac{2\pi}{T}\]
\[\omega=\frac{2(3.14)}{86400s}\]
\[\omega=7.268\times{10}^{-5}s^{-1}\]
Part (b)
Angular Speed $\omega$ is considered positive if the rotation is anti-clockwise and it is considered negative if the rotation is clockwise.
If the earth is observed from a point directly above the north pole, the rotation is anti-clockwise, hence the Angular Speed $\omega$ is positive.
Part (c)
The Linear speed $v$ of an object that is in rotation is given by:
\[v=R\omega\]
At the Equator, the distance between the axis of rotation of the earth and the point at the equator is the radius $R$ of the earth. So, substituting the values in the above equation:
\[v=(6.37\times{10}^6m)(7.268\times{10}^{-5}s^{-1})\]
\[v=463\frac{m}{s}\]
Part (d)
For a point that lies halfway between the north pole and equator of the earth, the radius $r$ from the rotational axis is calculated from the following diagram:
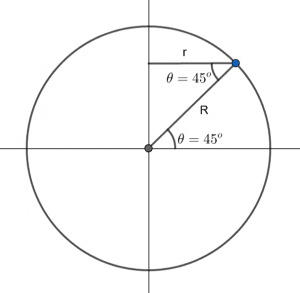
Figure 1
\[r=Rsin\theta\]
\[r=(6.37\times{10}^6m)sin{45}^\circ\]
\[r=(6.37\times{10}^6m)(0.707)\]
\[r=4.504{\times10}^6m\]
And we know:
\[v=r\omega\]
\[v=(4.504{\times10}^6m)(7.268\times{10}^{-5}s^{-1})\]
\[v=327.35\frac{m}{s}\]
Numerical Result
Part (a) – The angular speed $\omega$ of the earth is:
\[\omega=7.268\times{10}^{-5}s^{-1}\]
Part (b) –Angular Speed $\omega$ is positive.
Part (c) – The speed $v$ of a point on the equator of earth is:
\[v=463\frac{m}{s}\]
Part (d) – If a point lies halfway between the north pole and equator of the earth, its speed is:
\[v=327.35\frac{m}{s}\]
Example
A car moving at $45\dfrac{km}{h}$ is taking a turn having a radius of $50m$. Calculate its angular velocity.
Solution
Speed of the Car $v=45\dfrac{km}{h}$
\[v=\frac{45\times1000}{60\times60}\frac{m}{s}\]
\[v=12.5\frac{m}{s}\]
Radius of the turn $r=50m$.
The Linear speed $v$ of an object that is in rotation is given by:
\[v=r\omega\]
So:
\[\omega=\frac{v}{r}\]
\[\omega=\frac{12.5\dfrac{m}{s}}{50m}\]
\[\omega=0.25s^{-1}\]
Image/Mathematical drawings are created in Geogebra
