Volume of Cubes – Explanation & Examples
The volume of a cube is defined as the number of cubic units occupied by the cube.
A cube is 3- dimensional shape with 6 equal sides, 6 faces, and 6 vertices in geometry. Each face of a cube is a square. In 3 – dimension, the cube’s sides are; the length, width, and height.
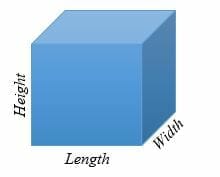
In the above illustration, sides of a cube are all equal i.e. Length = Width = Height = a
Cubes are everywhere! Common examples of cubes in the real world include square ice cubes, dice, sugar cubes, casserole, solid square tables, milk crates, etc.
The volume of a solid cube is the amount of space occupied by the solid cube. The volume is the difference in space occupied by the cube and the amount of space inside the cube for a hollow cube.
How to Find the Volume of a Cube?
To find the volume of a cube, here are the steps:
- Identify the length of the side or length of the edge.
- Multiply the length by itself three times.
- Write the result accompanied by the units of volume.
Volume is measured in cubic units, i.e., cubic meters (m3), cubic centimeters (cm3), etc. We can also measure the volume in liters or milliliters. In such cases, the volume is known as capacity.
Volume of a Cube Formula
The volume of cube formula is given by;
Volume of cube =length * width * height
V = a * a * a
= a3 cubic units
Where V= volume
a = The length of the edges.
Let’s try the formula with a few example problems.
Example 1
What is the volume of a cube whose sides are 10 cm each?
Solution
Given, the side length = 10 cm.
By the volume of a cube formula,
V = a3
Substitute a = 10 in the formula.
V = 103
= (10 x 10 x 10) cm3
= 1000 cm3
Therefore, the volume of the cube is 1000 cm3.
Example 2
The volume of a cube is 729 m3. Find the side lengths of the cube.
Solution
Given, volume, V = 729 m3.
a = ?
To get the side lengths of the cube, we find the cube root of the volume.
V = a3
729 = a3
3√ 729 = 3√ a3
a = 9
So, the length of cube is 9 m.
Example 3
The edge of a Rubik’s cube is 0.06 m. Find the volume of the Rubik’s cube?
Solution
Volume = a3
= (0.06 x 0.06 x 0.06) m3
= 0.000216 m3
= 2.16 x 10 – 4 m3
Example 4
A cubical box of external dimensions 100 mm by 100 mm by 100 mm is open at the top. Suppose the wooden box is made of 4 mm wood thick. Find the volume of the cube.
Solution
In this case, subtract the thickness of the wooden box to get the dimensions of the cube.
Given, the cube is open at the top, so we have
Length = 100 – 4 x 2
= 100 – 8
= 92 mm.
Width = 100 – (4 x 2)
= 92 mm
Height = (100 – 4) mm…………. (a cube is open at the top)
= 96 mm
Now calculate the volume.
V= (92 x 92 x 96) mm3
= 812544 mm3
= 8.12544 x 105 mm3
Example 5
Cubical bricks of length 5 cm are stacked such that the height, width, and length of the stack is 20 cm each. Find the number of bricks in the stack.
Solution
To get the number of bricks in the stack, divide the stack’s volume by the brick volume.
Volume of the stack = 20 x 20 x 20
= 8000 cm3
Volume of the brick = 5 x 5 x 5
= 125 cm3
Number of bricks = 8000 cm3/125 cm3
= 64 bricks.
Example 6
How many cubical boxes of dimensions 3 cm x 3 cm x 3 cm can be packed in a large cubical case of length 15 cm.
Solution
To find the number of boxes that can be packed in the case, divide the case’s volume by the volume of the box.
Volume of each box = (3 x 3 x 3) cm3
= 27 cm3
Volume of the cubical case = (15 x 15 x 15) cm3
= 3375 cm3
Number of boxes = 3375 cm3/27 cm3.
= 125 boxes.
Example 7
Find the volume of a metallic cube whose length is 50 mm.
Solution
Volume of a cube = a3
= (50 x 50 x 50) mm3
= 125,000 mm3
= 1.25 x 105 mm3
Example 8
The volume of a cubical solid disk 0.5 in3. Find the dimensions of the disk?
Solution
Volume of a cube = a3
0.5 = a3
a = 3√0.5
a = 0.794 in.
