JUMP TO TOPIC
Volume of Prisms – Explanation & Examples
The volume of a prism is the total space occupied by a prism. In this article, you will learn how to find a prism volume by using the volume of a prism formula.
Before we get started, let’s first discuss what a prism is. By definition, a prism is a geometric solid figure with two identical ends, flat faces, and the same cross-section all along its length.
Prisms are named after the shapes of their cross-section. For example, a prism with a triangular cross-section is known as a triangular prism. Other examples of prisms include rectangular prism. pentagonal prism, hexagonal prism, trapezoidal prism etc.
How to Find the Volume of a Prism?
To find the volume of a prism, you require the area and the height of a prism. The volume of a prism is calculated by multiplying the base area and the height. The volume of a prism is also measured in cubic units, i.e., cubic meters, cubic centimeters, etc.
Volume of a Prism Formula
The formula for calculating the volume of a prism depends on the cross-section or base of a prism. Since we already know the formula for calculating the area of polygons, finding the volume of a prism is as easy as pie.
The general formula for the volume of a prism is given as;
The volume of a Prism = Base Area × Length
Where Base is the shape of a polygon that is extruded to form a prism.
Let’s discuss the volume of different types of prisms.
Volume of a triangular prism
A triangular prism is a prism whose cross-section is a triangle.
The formula for the volume of a triangular prism is given as;
Volume of a triangular prism = ½ abh
where,
a = apothem of a triangular prism.
The polygon’s apothem is the line connecting the polygon center to the midpoint of one of the polygon’s sides. The apothem of a triangle is the height of a triangle.
b = base length of a triangle
h = height of a prism.
Example 1
Find the volume of a triangular prism whose apothem is 12 cm, the base length is 16 cm and height, is 25 cm.
Solution
By the formula of a triangular prism,
volume = ½ abh
= ½ x 12 x 16 x 25
= 150 cm3
Example 2
Find the volume of a prism whose height is 10 cm, and the cross-section is an equilateral triangle of side length 12 cm.
Solution
Find the apothem of the triangular prism.
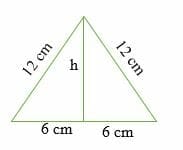
By Pythagorean theorem,
h2 + 62 =122
h2 + 36 =144
h2 = 108
h = 10.4 cm
Therefore, the apothem of the prism is 10.4 cm
Volume = ½ abh
= ½ x 10.4 x 12 x 10
= 624 cm3
Volume of a pentagonal prism
For a pentagonal prism, the volume is given by the formula:
Volume of a pentagonal prism = (5/2) abh
Where,
a = apothem of a pentagon
b = base length of a pentagonal prism
h = height of a prism.
Example 3
Find the volume of a pentagonal prism whose apothem is 10 cm, the base length is 20 cm and height, is 16 cm.
Solution
Volume of a pentagonal prism = (5/2) abh
= (5/2) x 10 x 20 x 16
= 8000 cm3
Volume of a hexagonal prism
A hexagonal prism has a hexagon as the base or cross-section. The volume of a hexagonal prism is given by:
Volume of a hexagonal prism = 3abh
where,
a = apothem length of a hexagon
b = base length of a hexagonal prism
h = height of a prism.
Example 4
Calculate the volume of a hexagonal prism with the apothem as 5 m, base length as 12 m, and height as 6 m.
Solution
Volume of a hexagonal prism = 3abh
= 3 x 5 x 12 x 6
= 1080 m3.
Alternatively, if the apothem of a prism is not known, then the volume of any prism is calculated as follows;
Volume of a prism = (h)(n) (s2)/ [4 tan (180/n)]
Where h = height of a prism
s = side length of the extruded regular polygon.
n = number of sides of a polygon
tan = tangent:
NOTE: This formula is only applied where the base or the cross-section of a prism is a regular polygon.
Example 5
Find the volume of a pentagonal prism with a height of 0.3 m and a side length of 0.1 m.
Solution
In this case, n = 5,
h = 0.3 m and s = 0.1 m
By substitution,
Volume of a pentagonal prism = (0.3) (5) (0.12)/ [4 tan (180/5)]
= 0.015/4 tan 36
= 0.015/2.906
= 0.00516 m3.
