Volume of Solids – Explanation & Examples

How to Find the Volume of a Solid?

The volume of a solid is the measure of how much space an object takes up. This article will show how to calculate the volume of a solid and the volume of regular and irregular solids.

The method for determining the volume of solid depends on its shape.  The volume of a solid is measured in cubic units, i.e., cubic centimeter, cubic meter, cubic feet, etc.

Volume of a Solid Formula

Here are the volume formulas for different regular solids:

• Rectangular prism

The volume of a rectangular prism is equal to the product of base area (length times width) and the height of the prism:

Volume of a solid rectangular prism = l x w x h

• Cube

Since we know all sides or edges of a cube are equal in length, then a cube’s volume is equal to any side, or edge cubed.

Volume of a cube = a³

• Prism

The volume of a prism is equal to the base area’s product and the height of a prism.

Volume of a prism = Base area x height

= B x h

• Cylinder

The volume of a cylinder is equal to the area of its circular base and a cylinder’s height.

Volume of a cylinder = πr²h

• Pyramid

The volume of a pyramid is equal to one -third the product of its base area and its height.

Volume of a pyramid = 1/3Bh

• Square pyramid

For a square pyramid, the volume is given as:

Volume =1/3s²h

Where s is the side length of the base and h is the height of the pyramid.

• Rectangular pyramid

The volume of a rectangular pyramid = 1/3 l w h

• Sphere

For a sphere, the volume is given as:

Volume of a sphere = 4/3 πr³

• Cone

Since a cone is a pyramid whose base is circular, therefore, the volume of a cone is:

Volume = 1/3 πr²h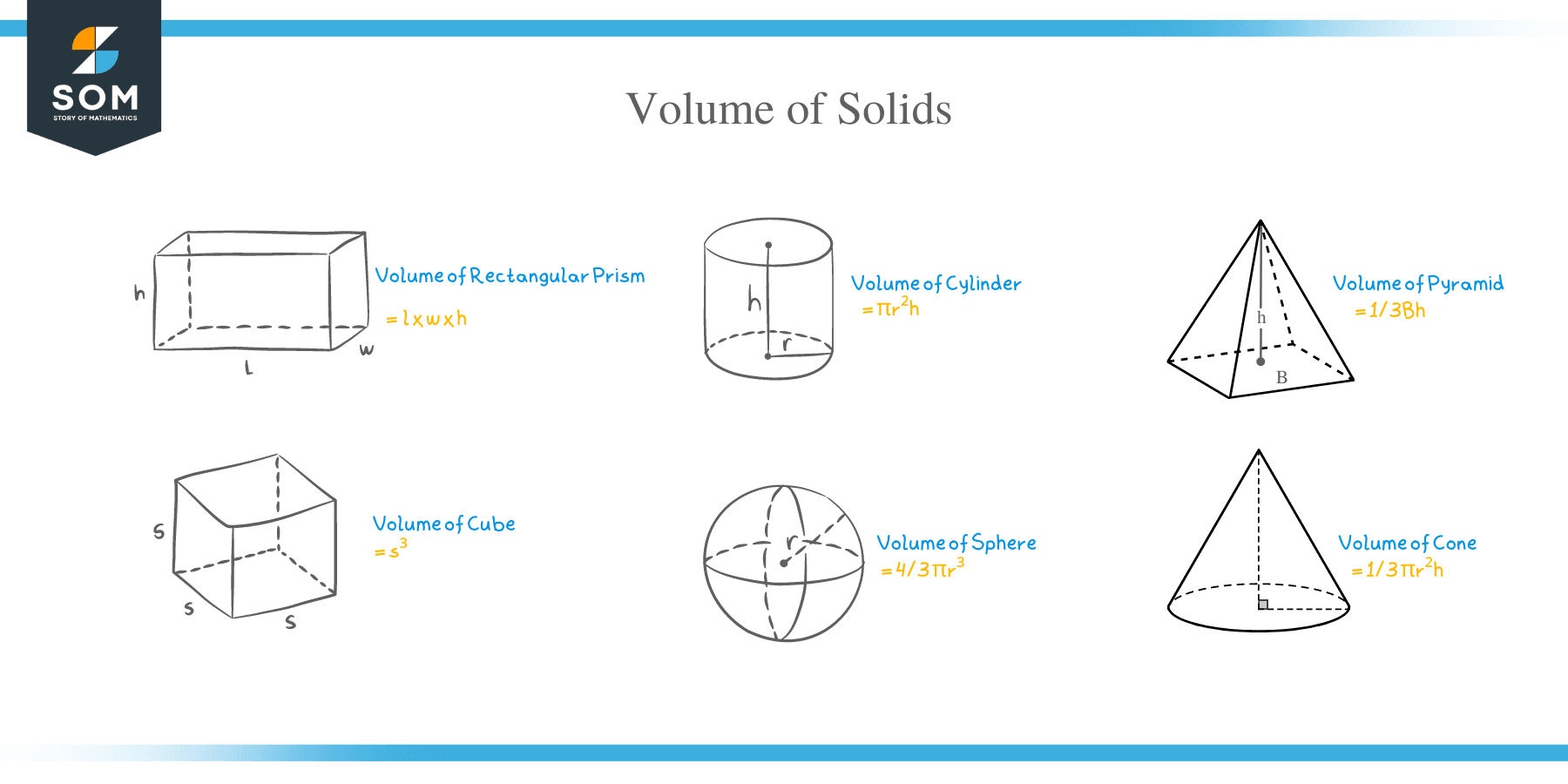

The volume of irregular solids

Since not all solids are regular in shape, their volumes cannot be determined using a volume formula.

In this case, the volume of irregular shaped solids can be found by water displacement method:

An irregular-shaped solid is dropped into a graduated cylinder filled with water.

The volume of the solid is then found by determining the difference between the initial and final readings of the graduated cylinder.

The water displacement method of finding the volume of irregular shaped solids is only suitable if: a solid does not absorb water and also if a solid does not react with water.

Alternatively, you can find the volume of an irregular shaped object by applying the following steps:

• First, break down the irregular solid into regular shapes whose volume can be calculated.
• Calculate the partial volumes of the small shapes
• Add up the partial volumes to get the total volume of the irregular-shaped solid.

Worked examples:

Example 1

Compare the volume of a solid sphere with a radius of 2 cm and a solid square pyramid with a base length of 2.5 cm and a height of 10 cm.

Solution

By the formula, volume of a sphere = 4/3 πr³

= 4/3 x 3.14 x 2 x 2 x 2

= 33.49 cm³

And the volume of a square pyramid = 1/3s²h

= 1/3 x 2.5 x 2.5 x 10

= 20.83 cm³

Therefore, the sphere is larger by volume than the pyramid.

Example 2

A cylindrical tank of radius 3 m and height 10 has a hemispherical lid of radius 3 m on the top. Find the volume of the tank.

Solution

First, calculate the volume of the cylindrical part of the tank.

Volume of a cylinder = π r² h

= 3.14 x 3 x 3 x 10

= 282.6 m³

Volume of the hemisphere = 2/3 πr³

= 2/3 x 3.14 x 3 x 3 x 3

= 56.52 m³

The total volume of the tank = volume of the cylinder + volume of the hemisphere

= 282.6 m³ + 56.52 m³

= 339.12 m³

Example 3

A truncated square pyramid has a height of 15 cm. Suppose the truncated pyramid’s base length and top lengths are 8 cm and 4 cm, respectively. Find the volume of the truncated pyramid.

Solution

A truncated pyramid is an example of a frustum.

Let the initial height of the pyramid = x

By similar triangles

x/ x – 15 = 8/4

4x = 8x – 120

–4x = –120

x = 30

Therefore, the height of the pyramid before truncation was 30 cm

Now, find the volume of the full pyramid

Volume = 1/ 3 x 8 x 8 x 30

= 640 cm³

Volume of the chopped off part of the pyramid = 1/3 x 4 x 4 x (30 – 15)

= 1/3 x 16 x 15

= 80 cm³

So, the volume of the truncated pyramid = (640 – 80) cm³

= 560 cm³.