Volume of Spheres – Explanation & Examples
The sphere is an extended version of a circle. Or it will be right to say a 3D version of a circle. In geometry, a sphere is a 3-dimensional round solid figure in which every point on its surface is equidistant from its center.
Common examples of objects which spherical in shape include balls, globes, ball bearings, water drops, bubbles, planets, etc.
In this article, we discuss how to find the volume of a sphere using the volume of a sphere formula.
How to Find the Volume of a Sphere?
The volume of a sphere is the amount of space occupied by it. For a hollow sphere like a football, the volume can be viewed as the number of cubic units required to fill up the sphere.
To find the volume of a sphere, you only need to know the radius of the sphere.
The volume of a sphere is measured in cubic units, i.e., m3, cm3, in3, ft3, etc.
Volume of a sphere formula
The volume of a sphere formula is given as:
Volume of a sphere = 4/3 πr3
where, π = 3.14 and r = radius of a sphere.
A half of a sphere is known as a hemisphere. The volume of a hemisphere is equal to half the volume of a sphere i.e.
Volume of a hemisphere = ½ (4/3) πr3
= 2/3 πr3
The volume of a sphere formula is attributed to Archimedes Principle, which states that:
When a solid object is completely submerged in a container filled with water, the displaced water volume is equal to the volume of the spherical solid object.
Let’s gain an insight into the volume of a sphere formula by solving a couple of example problems.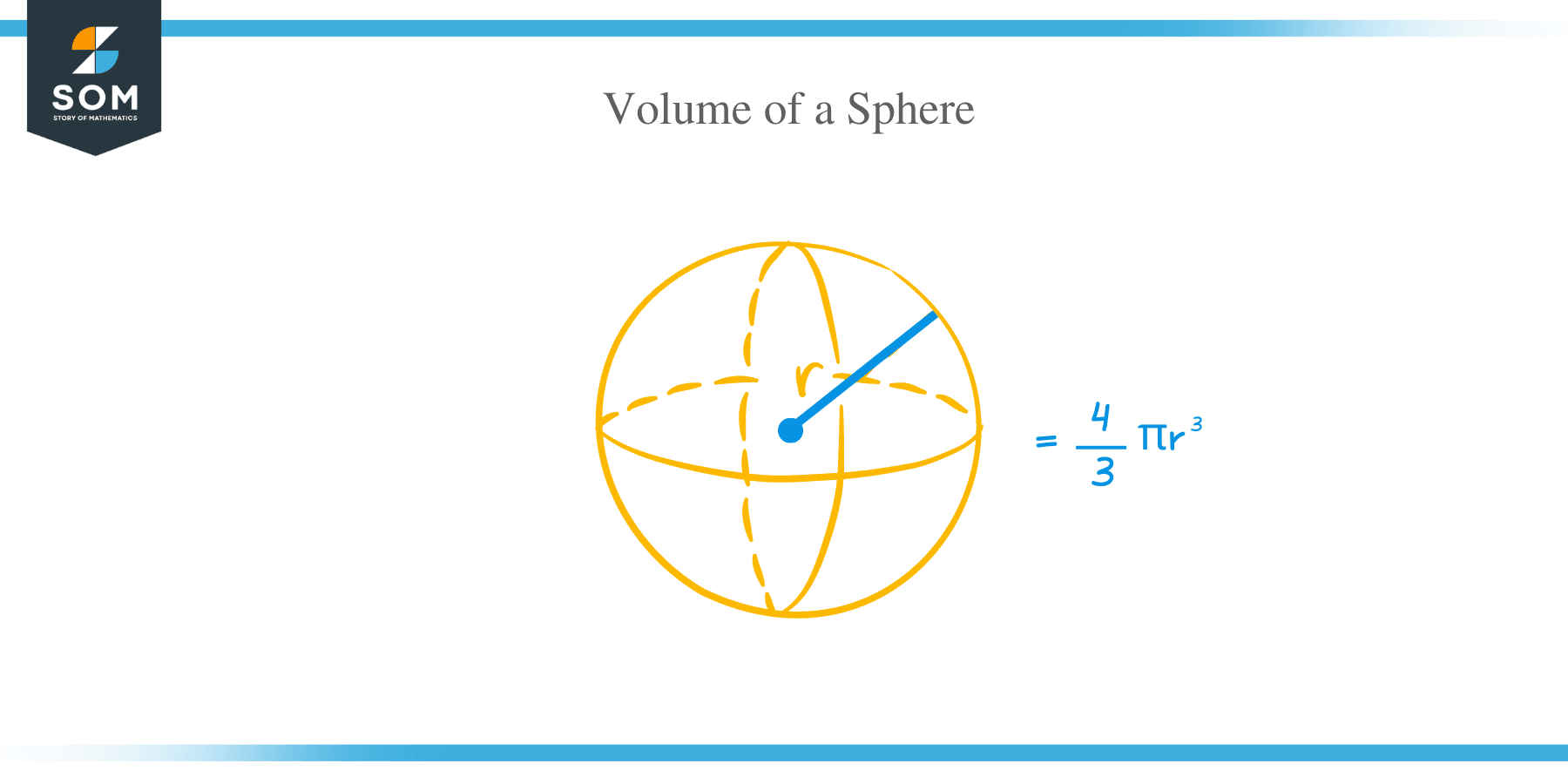
Example 1
Find the volume of a sphere whose radius is 5 cm.
Solution
By, the volume of a sphere formula, we have
V = 4/3 πr3
= (4/3) x 3.14 x 53
= (4/3) x 3.14 x 5 x 5 x 5
= 523.3 cm3
Example 2
What is the volume of a sphere with a radius of 24 mm?
Solution
Since we know the radius is half of the diameter, then
r = 24/2 = 12 mm
Volume of a sphere = 4/3 πr3
By substitution, we get
V = (4/3) x 3.14 x 12 x 12 x 12
= 7734.6 mm3
Example 3
The volume of a sphere is 523 cubic yards. Find the radius of the sphere.
Solution
Given, V = 523 cubic yards
Volume of a sphere, V = 4/3 πr3
523 = (4/3) x 3.14 x r3
523 = 4.19r3
Divide both sides by 4.19
r3 = 124.82
3√r3 = 3√124.82
r = 5
So, the radius of the sphere is 5 yards.
Example 4
A spherical solid metal of a radius of 8 cm is melted down into a cube. What will be the dimensions of the cube?
Solution
Equate the volume the sphere to the volume of the cube
4/3 πr3 = a3
4/3 x 3.14 x 8 x 8 x 8 = a3
2143.6 = a3
3√2143.6 =3√a3
a =12.9
Therefore, the sides of the cube will be 12.9 cm.
Example 5
The radius of an inflated spherical balloon is 7 feet. Suppose air is leaking from the balloon at a constant rate of 26 cubic feet per minute. How long will it take for the balloon to be completely deflated?
Solution
Volume of the spherical balloon = 4/3 πr3
= 4/3 x 3.14 x 7 x 7 x 7
= 1436.03 cubic feet
Divide the volume of the balloon by the rate of leakage
Time in minutes = 1436.03 cubic feet/26 cubic feet
= 55 minutes
Example 6
What will be the radius of a sphere with the same volume as a rectangular prism of length 5 mm, width, 3 mm, and height 4 mm?
Solution
Equate the volume of the rectangular prism to the volume of the sphere.
Volume of the prism = 5 x 3 x 4
= 60 mm3
Therefore,
60 = 4/3 πr3
60 = 4/3 x 3.14 x r3
60 = 4.19r3
r3 = 14.33
r = 3√14.33
r = 2.43
Hence, the radius of the sphere will be 2.43 mm.
Example 7
The water level in a cylindrical container of radius 0.5 m is 3.2 m. When a spherical solid object is completely submerged in the water, the water level rises by 0.6 m. Find the volume of the sphere.
Solution
The volume of the displaced water = volume of the sphere.
Volume of the displaced water in the cylinder = πr2h
= 3.14 x 0.5 x 0.5 x 0.6
= 0.471 m3.
Example 8
The volume of a typical baseball is 230 cm3. Find the radius of the ball.
Solution
Volume of a sphere = 4/3 πr3
230 = 4/3 x 3.14 x r3
230 = 4.19r3
r3 = 54.9
r = 3√54.9
r = 3.8
Thus, the radius of the baseball is 3.8 cm
Example 9
Find the volume of a hemisphere whose diameter is 14 in.
Solution
Volume of a hemisphere = 2/3 πr3
V = 2/3 x 3.14 x 7 x 7 x 7
= 718 cubic inches
