• Home
  • >
  • 14 Times Table – Explanation & Examples

14 Times Table – Explanation & Examples

14 Times TableThe 14 times table is the multiplication table of the number 14, and it is generated by multiplying the number 14 by the natural numbers. It is important to learn and memorize the 14 times table as it is used to solve complex multiplication and division problems.

The 14 times table is a table that contains the multiples of the number 14.

In this topic, we will present tips and tricks that will help you quickly learn and memorize the 14 times table.

You should refresh the following concepts to understand the material discussed here.

  1. Basics of addition and multiplication
  2. Multiplication table of 4
  3. Multiplication table of 7
  4. Multiplication table of 10

14 Multiplication Table

The table of 14 can be written as:

  • $14 \times 1 = 14$
  • $14 \times 2 = 28$
  • $14 \times 3 = 42$
  • $14 \times 4 =56$
  • $14 \times 5 =70$
  • $14 \times 6 =84$
  • $14 \times 7 = 98$
  • $14 \times 8 = 112$
  • $14 \times 9 = 126$
  • $14 \times 10 = 140$

Different Tips for the 14 Times Table:

The 14 times table is easy to understand and memorize if you know certain tips and patterns. Let us look at some simple tips which can help you memorize this table.

Digits Pattern of the 4 Times Table: The unit digits of the first 10 multiples of the 14 times table are the same as those of the 4 times table. If you have memorized the 4 times table, it will be easier for you to memorize the 14 times table. The digits pattern is shown in the picture below.

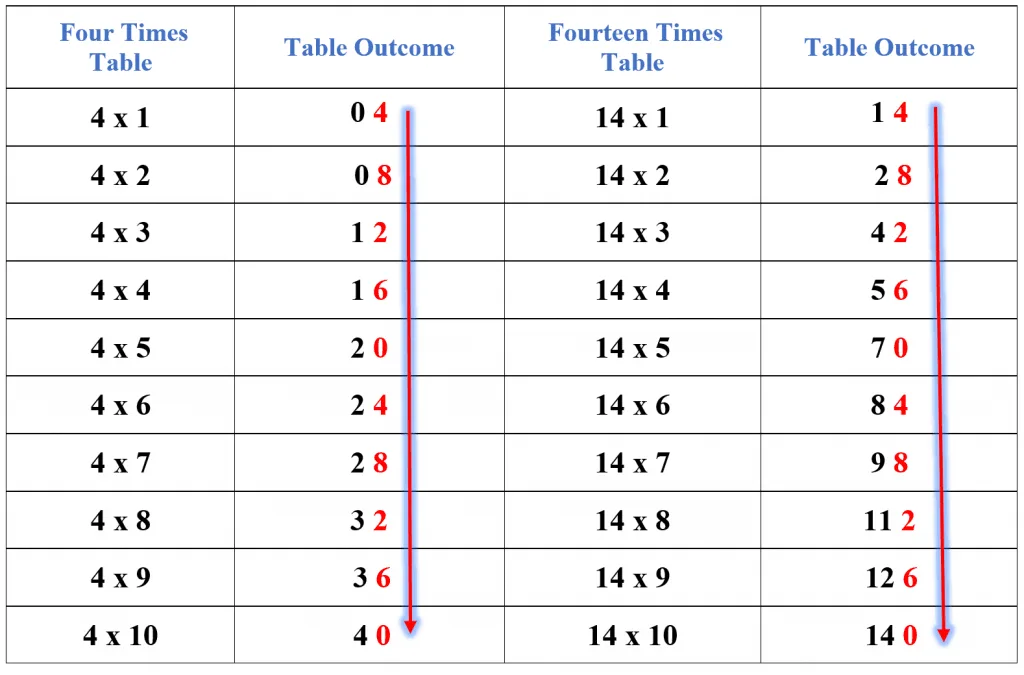
14 times table example

Using the 10 and the 4 Times Table: This is one of the easiest approaches to help you memorize the 14 times tables. It requires the usage of the 10 and the 4 times tables, so it will also help you revise these tables. In this method, you have to add the multiples of the number 10  to the multiples of the number 4, and the outcome of this addition will be the 14 times table. For example, the third multiple of 10 is 30, and the third multiple of 4 is 12, and if we add 30 and 12, we get 42 which is the third multiple of 14. The detailed method is presented in the table below.

10 Times Table

4 Times TableAddition

Outcome

 $10\times 1 = {\color{green}10}$

$ 4 \times 1 = {\color{red}4}$${\color{green}10}+  {\color{red}4}$

$14$

$10\times 2 = {\color{green}20}$

$4 \times 2 = {\color{red}8}$${\color{green}20}+ {\color{red}8}$

$28$

$10\times 3 = {\color{green}30}$

$4 \times 3 = {\color{red}12}$${\color{green}30} + {\color{red}12}$

$42$

$10\times 4 = {\color{green}40}$

$4 \times 4 = {\color{red}16}$${\color{green}40}+ {\color{red}16}$

$56$

$10\times 5 = {\color{green}50}$

$4\times 5 = {\color{red}20}$${\color{green}50} +{\color{red}20}$

$70$

$10\times 6 = {\color{green}60}$

$4\times 6 = {\color{red}24}$${\color{green}60} +{\color{red}24}$

$84$

$10\times 7 = {\color{green}70}$

$4 \times 7 = {\color{red}28}$${\color{green}70} +{\color{red}28}$

$98$

$10\times 8 = {\color{green}80}$

$4 \times 8 = {\color{red}32}$${\color{green}80} + {\color{red}32}$

$112$

$10\times 9 = {\color{green}90}$

$4 \times 9 = {\color{red}36}$${\color{green}90} + {\color{red}36}$

$126$

$10\times 10 = {\color{green}100}$

$4 \times 10 = {\color{red}40}$${\color{green}100} + {\color{red}40}$

$140$

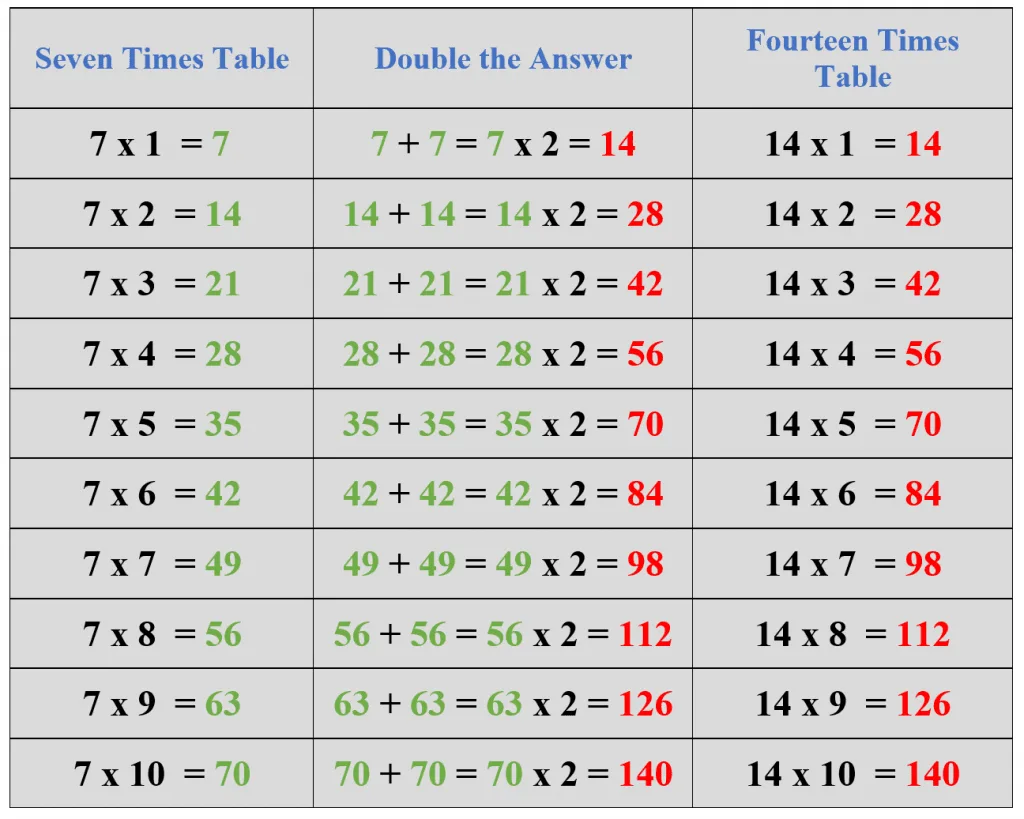
Using the 7 Times Table: The 7 times table can learn and memorize the 14 times table. This method will also help you in the revision of the 7 times table. First, we write the 7 times table, and then we add the values of the table to itself or multiply the values by 2. The results will be multiples of the number 14. For example, the fifth multiple of 7 is 35. If we double its value, i.e., $35\times2 = 70$ or add the multiple to itself, i.e., $35+35 = 70$, the answer 70 is the fifth multiple of the number 14. The detailed method is presented below in the table.

14 times table tip1

Digits Pattern: The 14 times table follows a digit pattern of five multiples. The digit pattern repeats itself after every five multiples of the number 14. In this pattern, the unit digits of the first five multiples are 4, 8, 2, 6, and 0. The same sequence is repeated for the next five multiples and so on. This pattern is shown in the table below.

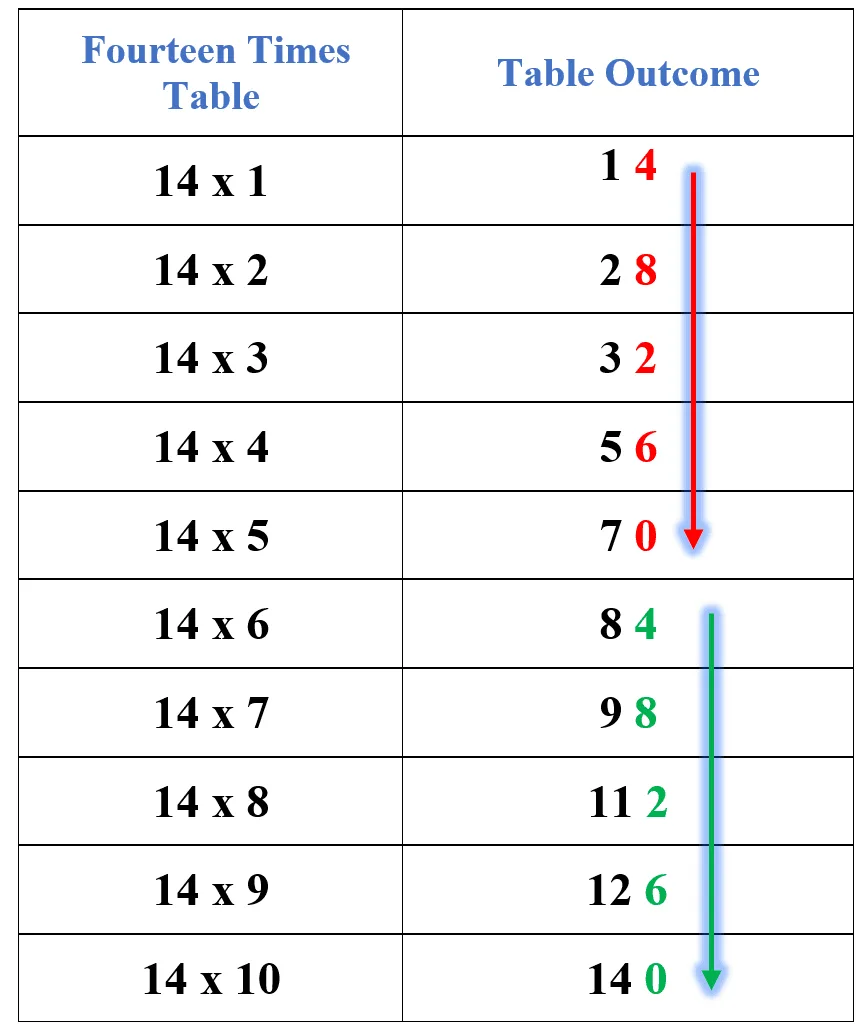
14 times table pattern

Table of 14 from 1 to 20:

A complete table of 14 from 1 to 20 can be written as:

Numerical Representation

Descriptive Representation

Product (Answer)

$14 \times 1$

Fourteen times one

$14$

$14 \times 2$

Fourteen times two

$28$

$14 \times 3$

Fourteen times three

$42$

$14 \times 4$

Fourteen times four

$56$

$14 \times 5$

Fourteen times five

$70$

$14 \times 6$

Fourteen times six

$84$

$14 \times 7$

Fourteen times seven

$98$

$14 \times 8$

Fourteen times eight

$112$

$14 \times 9$

Fourteen times nine

$126$

$14 \times 10$

Fourteen times ten

$140$

$14 \times 11$

Fourteen times eleven

$154$

$14 \times 12$

Fourteen times twelve

$168$

$14 \times 13$

Fourteen times thirteen

$182$

$14 \times 14$

Fourteen times fourteen$196$

$14 \times 15$

Fourteen times fifteen

$210$

$14 \times 16$

Fourteen times sixteen

$224$

$14 \times 17$

Fourteen times seventeen

$238$

$14 \times 18$

Fourteen times eighteen

$252$

$14 \times 19$

Fourteen times nineteen

$266$

$14 \times 20$

Fourteen times twenty

$280$

 

Example 1:  Calculate 14 times 11 minus 150 plus 40.

Solution:

14 times 11 minus 150 plus 40 can be written as:

$ = (14\times 11) – 150 + 40$

$ = 154 – 150 + 40$

$ = 4 +40 $

$ = 44 $

Example 2:  Calculate 14 times 11 minus 150 plus 10 times 14.

Solution:

14 times 11 minus 150 plus 10 times 14 can be written as:

$ = 14\times11 – 150 + 10\times 14$

$ = 154 – 150 + 140$

$ = 4 + 140$

$ = 144$

Example 3: Ellena has 100 sweaters in her shop. If she sells six sweaters daily, calculate the remaining number of sweaters at the end of 2 weeks.

Solution:

First, we calculate the total number of sweaters sold in 2 weeks using the 14 times table. Ellena sells six sweaters daily, so the total number of sweaters sold in 2 weeks will be  $14\times 6 = 84$. If we subtract 84 from the total number of sweaters, we will get the remaining number, i.e., $100 – 84 = 16$ sweaters.

Example 4: Verify whether the ninth multiple of the number 14 is 126 or not?

Solution:

We know the first 10 multiples of 14 are 14, 28, 42, 56, 70, 84, 98, 112, 126, and 140.

So, the ninth multiple of the number 14 is 126. Hence, 126 is the ninth multiple of 14.

Practice Questions:

  1. Danial eats 2 chocolates daily. How many chocolates will Danial eat at the end of 2 weeks?
  2. Find the value of “Y” if “$ Y \times 14 = 14 \times 10 + 140 – 11\times 14$.’’
  3. Subtract the sum of the first 5 even multiples of the number 14 from the first 5 odd multiples of the number 14.
  4. From the given table, select the numbers which are multiples of 14.
11713716216050516180
25192001811422467168
1541113017121720399221
150131161643010433129
219235276125218741280
132140562970882928
110323934356916319
31126261398010015931
4165435145122210157
4943984990132215109

Answer Key:

1). We know that 1 week = 7 days, so 2 weeks has $7 +7 = 14$ days. Danial eats 2 chocolates daily, and we can calculate the total number of chocolates Danial eats in 2 weeks by using the 14 times table

$14\times 2 = 28$ chocolates

2). $ Y \times 14 = 14 \times 10 + 140 – 11\times 14$

$ Y \times 14 = 140 + 140 – 154 $

$ Y \times 14 = 280 – 154 $

$ Y \times 14 =  126 $

We know $14 \times 9 =126$

$ Y = 9 $

3). We know that the first 5 odd multiples of 14 are 14, 42, 70, 98, and 126.

The first 5 even multiples of 14 are 28, 56, 84, 112, and 140.

Sum of the odd multiples of the number 14 is $14 + 42 + 70 + 98 + 126 = 350$.

Sum of the even multiples of the number 14 is $28 + 56 + 84 + 112 + 140 = 420$.

The difference between the sum of the first 5 even and odd multiples is  $= 420 – 350 = 70$.

4).

11713716216050516180
25192001811422467168
1541113017121720399221
150131161643010433129
219235276125218741280
132140562970882928
110323934356916319
31126261398010015931
4165435145122210157
4943984990132215109