Absolute Value Inequalities – Explanation & Examples
The absolute value of inequalities follows the same rules as the absolute value of numbers. The difference is that we have a variable in the prior and a constant in the latter.
This article will show a brief overview of the absolute value inequalities, followed by the step-by-step method to solve the absolute value inequalities.
Finally, there are examples of different scenarios for better understanding.
What is Absolute Value Inequality?
Before we can learn how to solve absolute value inequalities, let’s remind ourselves about a number’s absolute value.
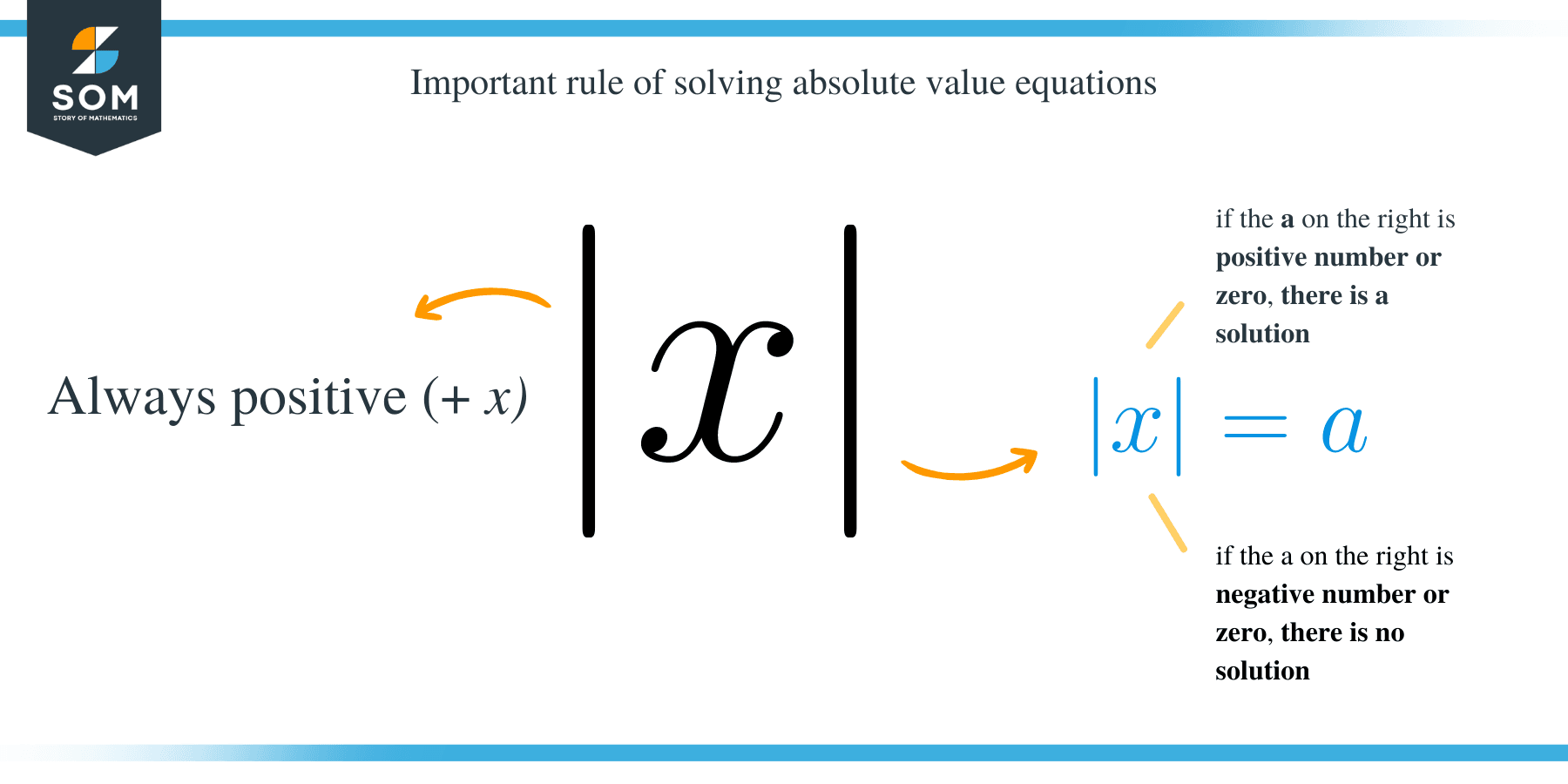
By definition, the absolute value of a number is the distance of a value from the origin, regardless of the direction. Absolute value is denoted by two vertical lines enclosing the number or expression.
For example, the absolute value of x is expressed as | x | = a, which implies that, x = +a and -a. Now let’s see what the absolute value inequalities entail.
An absolute value inequality is an expression with absolute functions as well as inequality signs. For example, the expression |x + 3| > 1 is an absolute value inequality containing a greater than symbol.
There are four different inequality symbols to choose from. These are less than (<), greater than (>), less than or equal (≤), and greater than or equal (≥). So, the absolute value inequalities can possess any one of these four symbols.
How to Solve Absolute Value Inequalities?
The steps for solving absolute value inequalities are much similar to solving absolute value equations. However, there is some extra information you need to keep in mind when solving absolute value inequalities.
The following are the general rules to consider when solving absolute value inequalities:
- Isolate on the left the absolute value expression.
- Solve the positive and negative versions of the absolute value inequality.
- When the number on the other side of the inequality sign is negative, we either conclude all real numbers as the solutions, or the inequality has no solution.
- When the number on the other side is positive, we proceed by setting up a compound inequality by removing the absolute value bars.
- The type of inequality sign determines the format of the compound inequality to be formed. For instance, if a problem contains greater than or greater than/equals to sign, set up a compound inequality that has the following formation:
(The values within absolute value bars) < – (The number on the other side) OR (The values within absolute value bars) > (The number on the other side).
- Similarly, if a problem contains a less than or less than/equals to sign, set up a 3- part compound inequality of the following form:
– (The number on the other side of inequality sign) < (quantity within the absolute value bars) < (The number on the other side of the inequality sign)
Example 1
Solve the inequality for x: | 5 + 5x| − 3 > 2.
Solution
Isolate the absolute value expression by adding 3 to both sides of the inequality;
=> | 5 + 5x| − 3 (+ 3) > 2 (+ 3)
=> | 5 + 5x | > 5.
Now solve both the positive and negative “versions” of the inequality as follows;
We’ll assume absolute value symbols by solving the equation the normal way.
=> | 5 + 5x| > 5 → 5 + 5x > 5.
=> 5 + 5_x_> 5
Subtract 5 from both sides
5 + 5x (− 5) > 5 (− 5) 5x > 0
Now, divide both sides by 5
5x/5 > 0/5
x > 0.
Thus, x > 0 is one of the possible solutions.
To solve for negative version of the absolute value inequality, multiply the number on the other side of the inequality sign by -1, and reverse the inequality sign:
| 5 + 5x | > 5 → 5 + 5x < − 5 => 5 + 5x < -5 Subtract 5 from both sides => 5 + 5x ( −5) < −5 (− 5) => 5x < −10 => 5x/5 < −10/5 => x < −2.
x > 0 or x < −2 are the two possible solutions to the inequality. Alternatively, we can solve | 5 + 5x | > 5 using the formula:
(The values within absolute value bars) < – (The number on other side) OR (The values within absolute value bars) > (The number on other side).
Illustration:
(5 + 5x) < – 5 OR (5 + 5x) > 5
Solve the expression above to get;
x < −2 or x > 0
Example 2
Solve |x + 4| – 6 < 9
Solution
Isolate the absolute value.
|x + 4| – 6 < 9 → |x + 4| < 15
Since our absolute value expression has a less than inequality sign, we set up the a 3-part compound inequality solution as:
-15 < x + 4 < 15
-19 < x < 11
Example 3
Solve |2x – 1| – 7 ≥ -3
Solution
First, isolate the variable
|2x – 1| – 7≥-3 → |2x – 1|≥4
We will set up an “or” compound inequality because of the greater than or equal to sign in our equation.
2 – 1≤ – 4 or 2x – 1 ≥ 4
Now, solve the inequalities;
2x – 1 ≤ -4 or 2x – 1 ≥ 4
2x ≤ -3 or 2x ≥ 5
x ≤ -3/2 or x ≥ 5/2
Example 4
Solve |5x + 6| + 4 < 1
Solution
Isolate the absolute value.
|5x + 6| + 4 < 1 → |5x + 6| < -3
Since the number on the other side is negative, check also the opposite to determine the solution.
|5x + 6| < -3
Positive < negative (false). Therefore, this absolute value inequality has no solution.
Example 5
Solve |3x – 4| + 9 > 5
Solution
Isolate the absolute value.
|3x – 4| + 9 > 5 → |3x – 4| > -4
|5x + 6| < -3
Since, positive < negative (true). Therefore, the solutions to this absolute value inequality are all real numbers.
