Home
>
Algebra

Algebra

What is the value of x? The answer to this question usually requires some knowledge of algebra.

Algebra is a branch of mathematics that involves solving equations and inequalities to find an unknown quantity.

While that may sound abstract, most people use algebra every day without realizing it. They use it when they figure out how much time to budget for a lunch break or decide how many eggs to add to a recipe when making a double batch.

The unknown quantity of an algebraic equation is usually represented by a letter, called a variable. It is the use of variables that makes algebra distinct from regular arithmetic. The techniques used to find the value or range of values of the variable(s) are useful in higher levels of mathematics, including trigonometry and calculus.

This page includes resources for all algebra topics, beginning with the basics of algebraic expressions before moving onto solving equations with variables. After that, there are explanations of binomials, trinomials, and higher-order polynomials. This guide ends with information about functions.

Basic Algebra

The fundamental concepts of algebra revolve around writing algebraic expressions. These are mathematical statements that include a variable but no equal sign. These expressions express a quantity.

This topic begins with an introduction to algebra and algebraic expressions. It then goes on to explain how to put two or more expressions together with arithmetic operations and how to rewrite them in different forms.

Techniques for Solving Equations

The most important rule of solving equations in algebra is that anything done to one side of an equation must be done to the other. Otherwise, the equality does not hold. This principle is of great help in finding the value of variables.

This topic includes subtopics on different ways to do just that. It starts with the basic concepts that will be used, including isolating the variable and combining like terms, before showing how to use these concepts in specific equations. The topic ends with information on how to solve equations that require multiple steps and equations that include multiple variables.

Systems of Linear Equations

Algebraic equations can represent lines on a graph. The equations of two such lines can be analyzed to see if the lines intersect at all.

There are several different ways to do this, and this topic goes over all of them, beginning with the simplest method, substitution.

Inequalities

Sometimes, algebraic expressions are not equal. One may be greater than the other or vice versa. These types of relationships are called inequalities, and they are represented using the symbols >, <, ≥, and ≤. The solution of an inequality will typically be a range of values instead of a single value.

This section introduces inequalities and then gives strategies for solving them algebraically and graphically. It also includes steps for solving more complex inequalities such as compound inequalities and those that include absolute value signs.

Quadratic Equations

Quadratic equations include a variable that is squared, such as x^2. Factoring quadratic equations into binomials, expressions involving two terms, can give more information about the graph of the equation.

This topic begins with strategies for factoring simple quadratics. It then moves onto strategies for more complex quadratics. The section ends with an explanation of how quadratic equations relate to their graphs.

Factoring Trinomials

Trinomials contain three expressions. While there is overlap between quadratic expressions and trinomials, they are not entirely the same. Trinomials may be expressions with multiple variables raised to the first power, or they can include variables raised to powers greater than two.

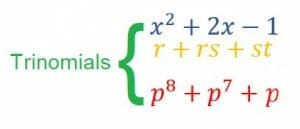
This section follows a similar format as the section about quadratics. It begins with simple methods for factoring trinomials before moving to more complex ones.

Polynomials

A polynomial is any mathematic expression with more than one term. It can include multiple variables raised to different, positive powers as well as constants.

This topic begins with strategies for using basic arithmetic operations to combine polynomials. It then discusses some strategies for factoring them in generic and specific circumstances.

Rational Expressions

A rational expression is one that is written as a fraction with an algebraic expression in both the numerator and denominator.

This guide begins with strategies for making rational expressions simpler. It also discusses how to combine them using addition, subtraction, multiplication, and division.

Logarithms

If addition is the opposite of subtraction and multiplication is the opposite of division, logarithms are the opposite of exponents. Logs will include a “base,” just like a regular exponent. The most famous logarithm has base e, and since it is used so frequently, this log has its own notation, ln. It is called “natural logarithm.”

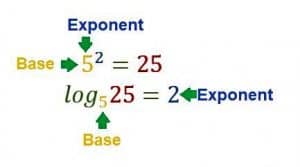
This section begins with an explanation of logarithms and how to work with them. It then goes on to explain how to solve equations with logarithms and how to graph them.

Functions

A function is any mathematical relationship for which any input has a maximum of one output. If a function is graphed, it will pass the “vertical line test,” because a vertical line passing over the function will never touch more than one point at a time. Lines, quadratics, and other polynomials are examples of functions.

This topic begins by describing functions and their properties. It then explains how to combine functions with arithmetic operations and composition. It ends with a discussion of function inverses.

Coordinate Geometry and Graphs

Equations with two variables can be graphed in the xy-plane. There are many techniques and strategies that can be used to derive an equation from a graph and vice versa.

This section begins with the basics of plotting points and graphing straight lines. The topic then explores how to find features of a line segment such as its length and midpoint. It also discusses how to graph more complex functions such as quadratic and exponential functions.