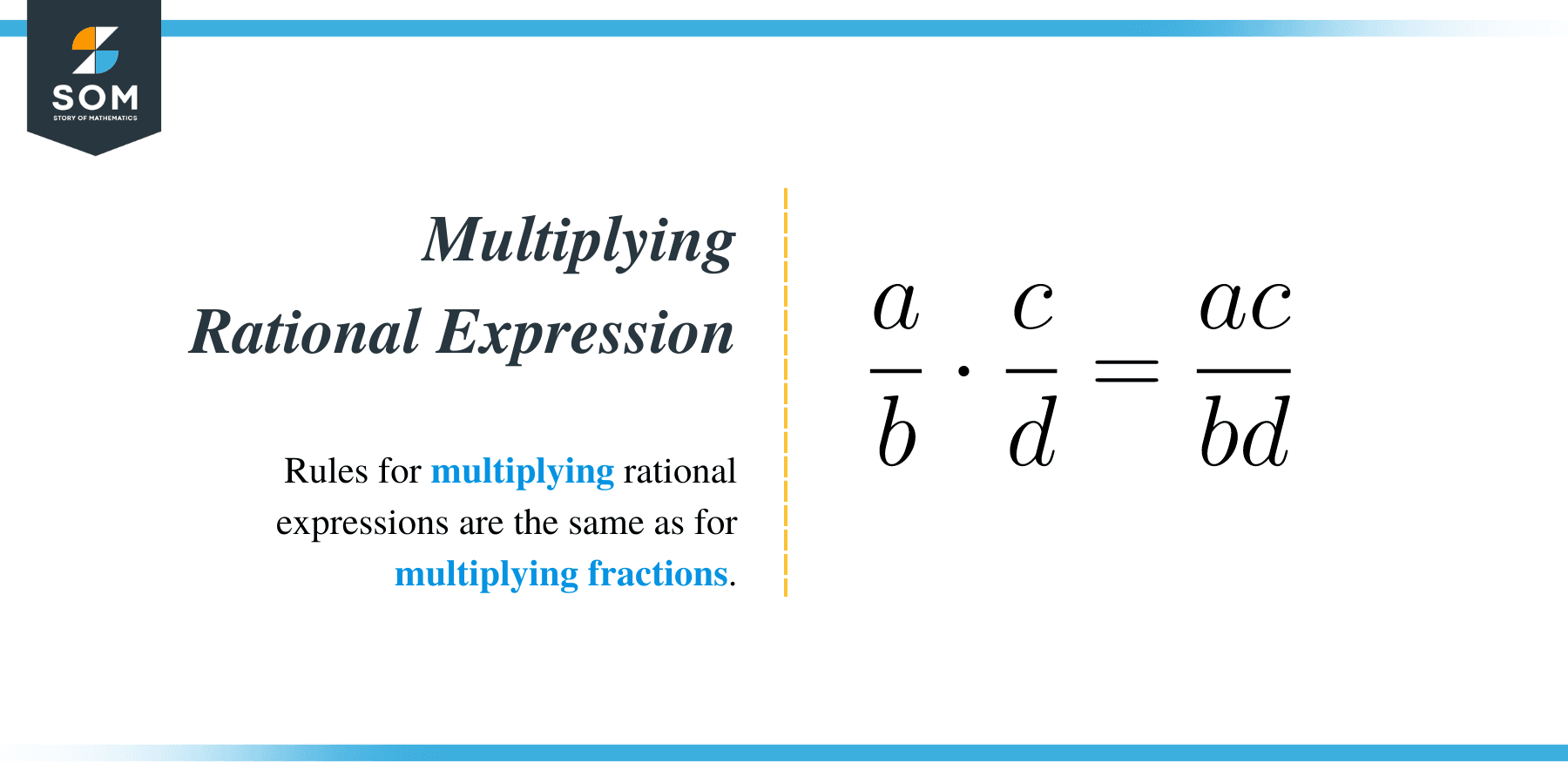Multiplying Rational Expressions – Techniques & Examples

To learn how to multiply rational expressions, let’s first recall the multiplication of numerical fractions.

Multiplication of fractions involves separately finding the product of numerators and the product of denominators of given fractions.

For instance, if a/b and c/d are any two fractions, then;

a/b × c/d = a × c/b × d. Let’s take a look at the examples below:

• Multiply 2/7 by 3/5

Solution

2/7 × 3/5

= 2 × 3/7 × 5= 6/35

• Multiply 5/9 by (-3/4)

Solution

5/9 × (-3/4)

= 5 × -3/9 × 4

= -15/36

= -5/12

Similarly, rational expressions are multiplied by following the same rule.

How to Multiply Rational Expressions?

To multiply rational expressions, we apply the steps below:

• Completely factor out denominators and numerators of both fractions.
• Cancel out common terms in the numerator and denominator.
• Now rewrite the remaining terms both in the numerator and denominator.

Use the algebraic identities below to help you in factoring the polynomials:

• (a² – b²) = (a + b) (a – b)
• (x² – 4²) = (x + 4) (x – 4)
• (x² – 2²) = (x + 2) (x – 2)
• (a³ + b³) = (a + b) (a² – a b + b²)

Example 1

Simplify (x² – 2x) / (x + 2) * (3 x + 6)/ (x – 2)

Solution

Factor the numerators,

(x² – 2x) / (x + 2) * (3 x + 6)/ (x – 2)

⟹ x (x – 2) / (x + 2) * 3(x + 2)/ (x – 2)

Cancel out common terms in numerators and denominators of both fractions to get;

⟹ 3x

Example 2

Solve [(x² – 3x – 4)/ (x² – x -2)] * [(x² – 4)/ (x² -+ x -20)]

Solution

First, factor the numerators and denominators of both fractions.

[(x – 4) (x + 1)/ (x + 1) (x – 2)] * [(x + 2) (x – 2)/ (x – 4) (x + 5)]

Cancel out common terms and rewrite the remaining terms

= x + 2/x + 5

Example 3

Multiply [(12x – 4x²)/ (x² + x – 12)] * [(x² + 2x – 8)/x³ – 4x)]

Solution

Factor the rational expressions.

⟹ [-4x (x – 3)/ (x – 3) (x + 4)] * [(x – 2) (x + 4)/x (x + 2) (x – 2)]

Reduce the fractions by cancelling common terms in the numerators and denominators to get;

= -4/x + 2

Example 4

Multiply [(2x² + x – 6)/ (3x² – 8x – 3)] * [(x² – 7x + 12)/ (2x² – 7x – 4)]

Solution

Factor the fractions

⟹ [(2x – 3) (x + 2)/ (3x + 1) (x – 3)] * [(x – 30(x – 4)/ (2x + 1) (x – 4)]

Cancel out common terms in the numerators and denominators and rewrite the remaining terms.

⟹ [(2x – 3) (x + 2)/ (3x + 1) (2x + 1)]

Example 5

Simplify [(x² – 81)/ (x² – 4)] * [(x² + 6 x + 8)/ (x² – 5 x – 36)]

Solution

Factor the numerators and denominators of each fraction.

⟹ [(x + 9) (x – 9)/ (x + 2) (x – 2)] * [(x + 2) (x + 4)/ (x – 9) (x + 4)]

On cancelling common terms, we get;

= (x + 9)/ (x – 2).

Example 6

Simplify [(x² – 3 x – 10)/ (x² – x – 20)] * [(x² – 2 x + 4)/ (x³ + 8)]

Solution

Factor out (x³ + 8) using the algebraic identity (a³ + b³) = (a + b) (a² – a b + b²).

⟹ (x³ + 8) = (x + 2) (x² – 2 x + 4).

⟹ (x² – 3 x – 10) = (x – 5) (x + 2)

⟹ (x² – x – 20) = (x – 5) (x + 4)

[(x² – 3 x – 10)/ (x² – x – 20)] * [(x² – 2 x + 4)/ (x³ + 8)] = [(x – 5) (x + 2)/ (x – 5) (x + 4)] * [(x² – 2 x + 4)/ (x + 2) (x² – 2 x + 4)]

Now, cancel out common terms to get;

= 1/ (x + 4).

Example 7

Simplify [(x + 7)/ (x² + 14 x + 49)] * [(x² + 8x + 7)/ (x + 1)]

Solution

Factor the fractions.

⟹ (x² + 14 x + 49) = (x + 7) (x + 7)

⟹ (x² + 8x + 7) = (x + 1) (x + 7)

= [(x + 7)/ (x + 7) (x + 7)] * [(x + 1) (x + 7)/ (x + 1)]

On cancelling common terms, we get the answer as;

= 1

Example 8

Multiply [(x² – 16)/ (x – 2)] * [(x² – 4)/ (x³ + 64)]

Solution

Use the algebraic identity (a² – b²) = (a + b) (a – b) to factor (x² – 16) and (x² – 4).

(x² – 4²) ⟹ (x + 4) (x – 4)

(x² – 2²) ⟹ (x + 2) (x – 2).

Also apply the identity (a³ + b³) = (a + b) (a² – a b + b²) to factor (x³ + 64).

(x³ + 64) ⟹ (x² – 4x + 16)

= [(x + 4) (x – 4)/)/ (x – 2)] * [(x + 2) (x – 2)/ (x² – 4x + 16)]

Cancel common terms to get;

= (x – 4) (x + 2)/ (x² – 4x + 16)

Example 9

Simplify [(x² – 9 y²)/ (3 x – 3y)] * [(x² – y²)/ (x² + 4 x y + 3 y²)]

Solution

Apply the algebraic identity (a²-b²) = (a + b) (a – b) to factor (x²- (3y) ² and (x² – y²)

⟹ (x²-(3y) ² = (x + 3y) (x-3y)

⟹ (x² – y²) = (x + y) (x – y).

Factor (x² + 4 x y + 3 y²)

= x² + 4 x y + 3 y²

= x² + x y + 3 x y + 3 y²

= x (x + y) + 3y (x + y)

= (x + y) (x + 3y)

Cancel common terms to get:

= (x – 3y)/3