Common and Natural Logarithms – Explanation & Examples
The logarithm of a number is the power or exponent by which another value must be raised to produce an equivalent value of the given number.
The concept of logarithms was introduced in the early 17th century by John Napier – a Scottish mathematician. Later, scientists, navigators, and engineers adopted the concept to perform computation using logarithmic tables.
The logarithm of a number is expressed in the form of;
log b N = x, where b is the base and can be any number except 1 and zero; x and N are the exponent and argument, respectively.
For example, the logarithm of 32 to base 2 is 5 and can be represented as;
log 2 32 = 5
Having learned about logarithms, we can note that the base of a logarithmic function can be any number except 1 and zero. However, the other two special types of logarithms are frequently used in mathematics. These are common logarithm and natural logarithm.
What is a Common Logarithm?
A common logarithm has a fixed base of 10. The common log of a number N is expressed as;
log 10 N or log N. Common logarithms are also known as decadic logarithm and decimal logarithm.
If log N = x, then we can represent this logarithmic form in exponential form, i.e., 10 x = N.
Common logarithms have a wide application in science and engineering. These logarithms are also called Briggsian logarithms because, in the 18th century, British mathematician Henry Briggs introduced them. For example, the acidity and alkalinity of a substance are expressed in exponential.
The Richter scale for measuring earthquakes and the decibel for sound is usually expressed in logarithmic form. It is so common that you can assume it to be log x or common log if you find no base written.
The basic properties of common logarithms are the same as the properties of all logarithms.
These include product rule, quotient rule, power rule, and zero exponent rule.
- Product rule
The product of two common logarithms is equal to the sum of individual common logarithms.
⟹ log (m n) = log m + log n.
- Quotient rule
The division rule of common logarithms states that the quotient of two common logarithmic values is equal to each common logarithm’s difference.
⟹ log(m/n) = log m – log n
- Power rule
The common logarithm of a number with an exponent is equal to the product of the exponent and its common logarithm.
⟹ log (m n) = n log m
- Zero Exponent Rule
⟹ log 1 = 0
What is a Natural Logarithm?
The natural logarithm of a number N is the power or exponent to which ‘e’ has to be raised to be equal to N. The constant ‘e’ is the Napier constant and is approximately equal to 2.718281828.
ln N = x, which is the same as N = e x.
Natural logarithm is mostly used in pure mathematics such as calculus.
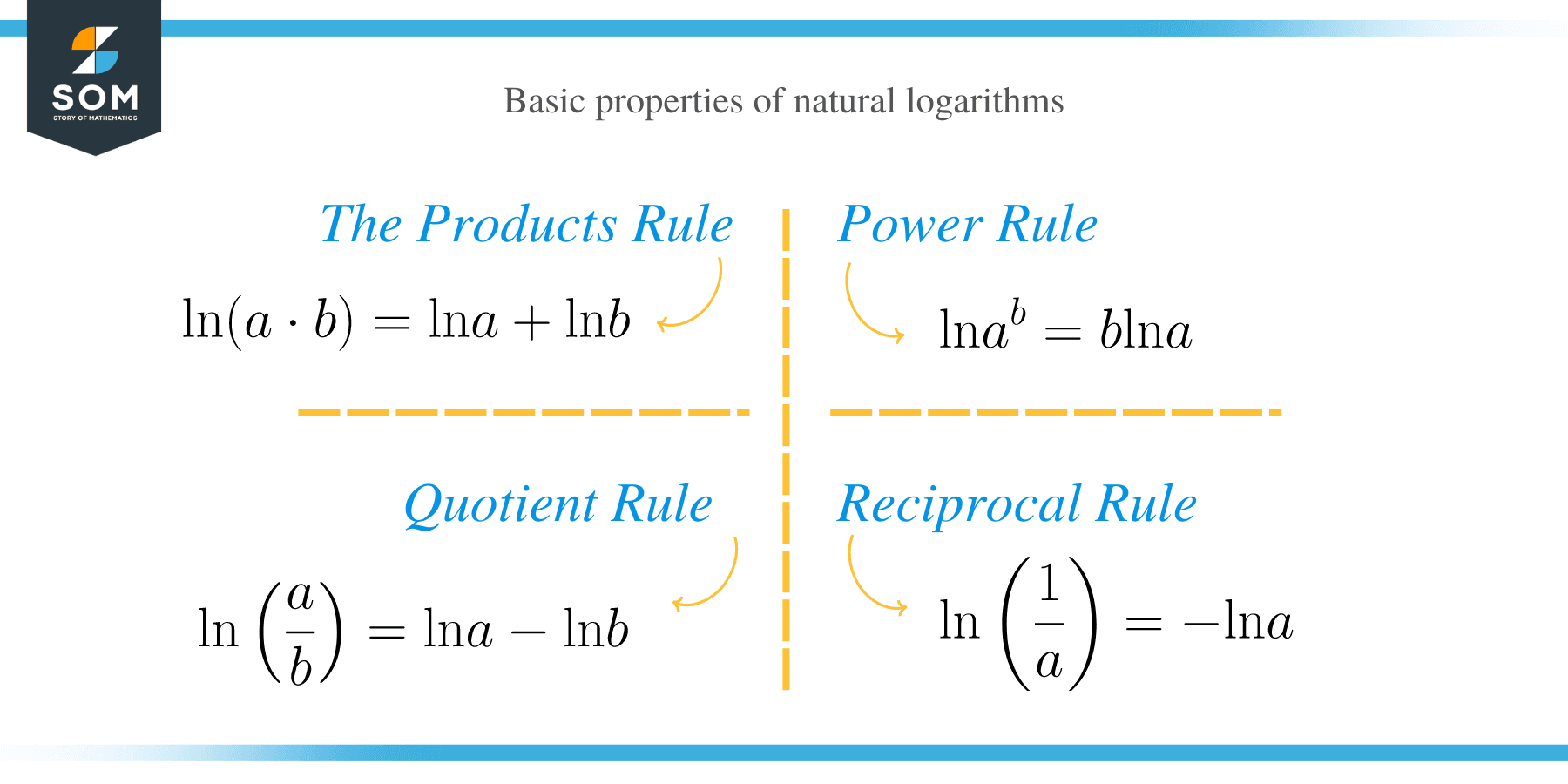
The basic properties of natural logarithms are same as the properties of all logarithms.
- Product Rule
⟹ ln (ab) = ln (a) + ln (b)
- Quotient Rule
⟹ ln (a/b) = ln (a) – ln (b)
- Reciprocal Rule
⟹ ln (1/a) = −ln (a)
- Power Rule
⟹ ln (a b) = b ln (a)
Other properties of natural log are:
- e ln (x) = x
- ln (e x) = x
- ln (e) = 1
- ln (∞) = ∞
- ln (1) = 0
Scientific and graphing calculators have keys for both common and natural logarithms. The key for the natural log is labeled “e” or “ln” while that of the common logarithm is labeled “log”.
Now, let’s check our understanding of the lesson by attempting a few problems of natural and common logarithms.
Example 1
Solve for x if, 6 x + 2 = 21
Solution
Express both sides in common logarithm
log 6 x + 2 = log 21
Applying the power rule of logarithms, we get;
(x + 2) log 6 = log 21
Divide both sides by log 6.
x + 2 = log 21/log 6
x + 2 = 0 .5440
x = 0.5440 – 2
x = -1.4559
Example 2
Solve for x in e2x = 9
Solution
ln e3x = ln 9
3x ln e = ln 9
3x = ln 9
isolate x by dividing both sides by 3.
x = 1/3ln 9
x = 0. 732
Example 3
Solve for x in log 0.0001 = x
Solution
Rewrite the common log. in exponential form.
10x = 0.0001
But 0.0001 = 1/10000 = 10-4
Therefore,
x = -4
