Simplifying Expressions – Explanation & Examples

Learning how to simplify an expression is the most important step in understanding and mastering algebra. Simplification of expressions is a handy mathematics skill because it allows us to change complex or awkward expressions into simpler and compact forms. But before that, we must know what an algebraic expression is.

An algebraic expression is a mathematical phrase where variables and constants are combined using the operational (+, -, × & ÷) symbols. For example, 10x + 63 and 5x – 3 are examples of algebraic expressions.

In this article, we shall learn a few tricks on how to simplify any algebraic expression.

How to Simplify Expressions?

Simplification of an algebraic expression can be defined as the process of writing an expression in the most efficient and compact form without affecting the value of the original expression.

The process entails collecting like terms, which implies adding or subtracting terms in an expression.

Let’s remind ourselves of some of the important terms used when simplifying an expression:

• A variable is a letter whose value is unknown in an algebraic expression.
• The coefficient is a numerical value used together with a variable.
• A constant is a term that has a definite value.
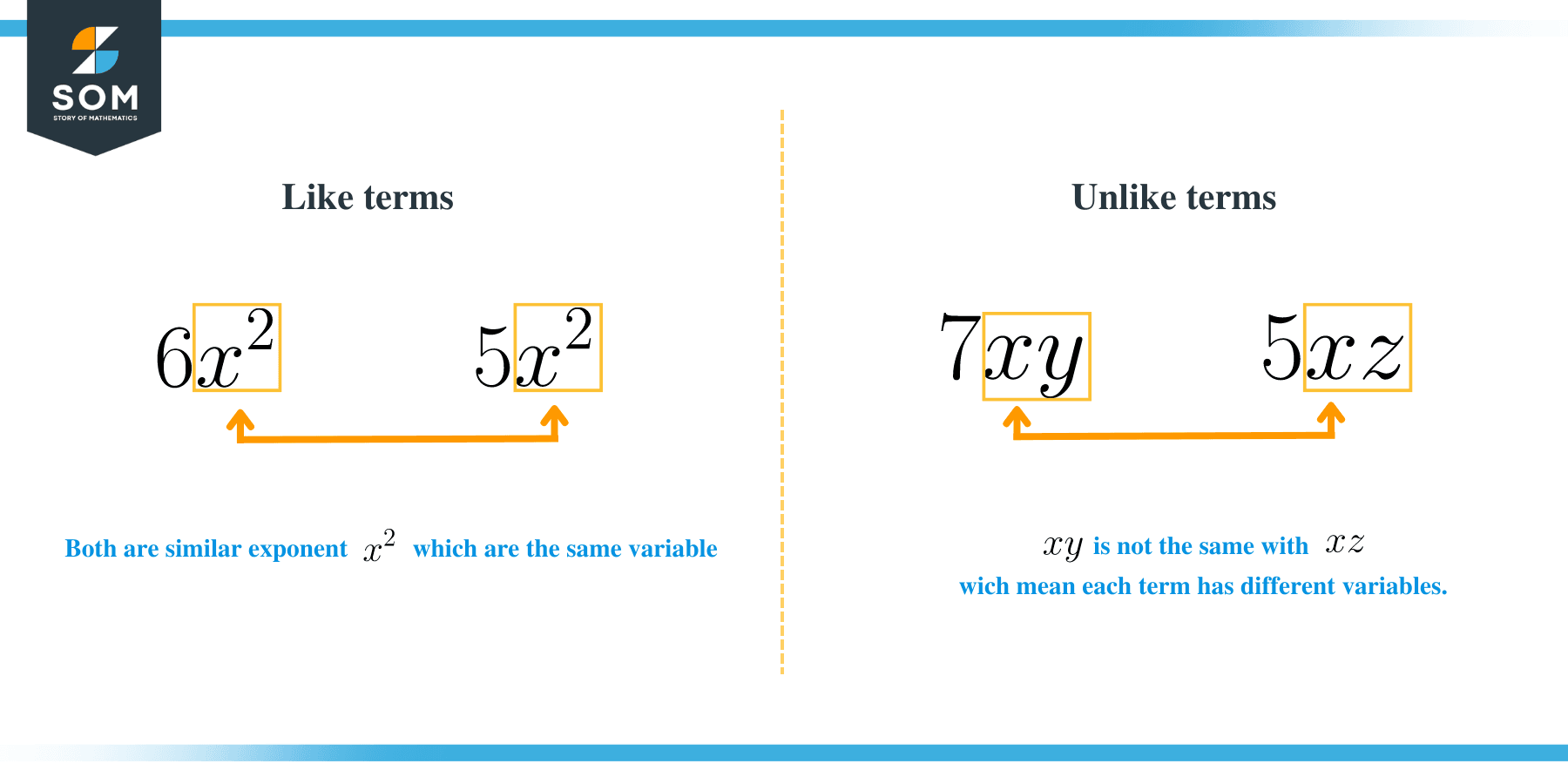
• Like terms are variables with the same letter and power. Like terms can sometimes contain different coefficients. For example, 6x²and 5x² are like terms because they have a variable with a similar exponent. Similarly, 7yx and 5xz are unlike terms because each term has different variables.

To simplify any algebraic expression, the following are the basic rules and steps:

• Remove any grouping symbol such as brackets and parentheses by multiplying factors.
• Use the exponent rule to remove grouping if the terms are containing exponents.
• Combine the like terms by addition or subtraction
• Combine the constants

Example 1

Simplify 3x² + 5x²

Solution

Since both terms in the expression are have same exponents, we combine them;

3x² + 5x² = (3 + 5) x² = 8x²

Example 2

Simplify the expression: 2 + 2x [2(3x+2) +2)]

Solution

First work out any terms within brackets by multiplying them out;

= 2 + 2x [6x + 4 +2] = 2 + 2x [6x + 6]

Now eliminate the parentheses by multiplying any number outside it;

2 + 2x [6x + 6] = 2 + 12x ² + 12x

This expression can be simplified by dividing each term by 2 as;

12x ²/2 + 12x/2 + 2/2 = 6 x ² + 6x + 1

Example 3

Simplify 3x + 2(x – 4)

Solution

In this case, it is impossible to combine terms when they are still in parentheses or any grouping sign. Therefore, eliminate the parenthesis by multiplying any factor outside the grouping by all terms inside it.

Hence, 3x + 2(x – 4) = 3x + 2x – 8

= 5x – 8

When a minus sign is in front of a grouping, it normally affects all the operators inside the parentheses. This means that a minus sign in front of a group will change the addition operation to subtraction and vice versa.

Example 4

Simplify 3x – (2 – x)

Solution

3x – (2 – x) = 3x + (–1) [2 + (–x)]

= 3x + (–1) (2) + (–1) (–x)

= 3x – 2 + x

= 4x – 2

However, if there is only a plus sign comes before the grouping, then the parentheses are simply erased.

For example, to simplify 3x + (2 – x), the brackets are eliminated as shown below:

3x + (2 – x) = 3x + 2 – x

Example 5

Simplify 5(3x-1) + x((2x)/ (2)) + 8 – 3x

Solution

15x – 5 + x(x) + 8 – 3x

15x – 5 + x² + 8 – 3x.

Now combine the like terms by adding and subtracting the terms;

x² + (15x – 3x) + (8 – 5)

x² + 12x + 3

Example 6

Simplify x (4 – x) – x (3 – x)

Solution

x (4 – x) – x (3 – x)

4x – x² – x (3 – x)

4x – x² – (3x – x²)

4x – x² – 3x + x² = x