- Home
- >
- Quadratic Formula – Explanation & Examples
JUMP TO TOPIC
Quadratic formula – Explanation & Examples
 By now, you know how to solve quadratic equations by methods such as completing the square, the difference of a square, and the perfect square trinomial formula.
By now, you know how to solve quadratic equations by methods such as completing the square, the difference of a square, and the perfect square trinomial formula.
In this article, we will learn how to solve quadratic equations using two methods, namely the quadratic formula and the graphical method. Before we can dive into this topic, let’s recall what a quadratic equation is.
What is a Quadratic Equation?
A quadratic equation in mathematics is defined as a polynomial of second degree whose standard form is ax2 + bx + c = 0, where a, b and c are numerical coefficients and a ≠ 0.
The term second degree means that at least one term in the equation is raised to the power of two. In a quadratic equation, the variable x is an unknown value, for which we need to find the solution.
Examples of quadratic equations are: 6x² + 11x – 35 = 0, 2x² – 4x – 2 = 0, 2x² – 64 = 0, x² – 16 = 0, x² – 7x = 0, 2x² + 8x = 0 etc. From these examples, you can note that, some quadratic equations lack the term “c” and “bx.”
How to use the quadratic formula?
Suppose ax2 + bx + c = 0 is our standard quadratic equation. We can derive the quadratic formula by completing the square as shown below.
Isolate the term c to right side of the equation
ax2 + bx = -c
Divide each term by a.
x2 + bx/a = -c/a
Express as a perfect square
x 2 + bx/a + (b/2a)2 = – c/a + (b/2a)2
(x + b/2a) 2 = (-4ac+b2)/4a2
(x + b/2a) = ±√ (-4ac + b2)/2a
x = – b/2a ±√ (b2 – 4ac)/2a
x = [- b ±√ (b2 – 4ac)]/2a………. (This is the quadratic formula)
The presence of the plus (+) and minus (-) in the quadratic formula implies that there are two solutions, such as:
x1 = (-b + √b2 – 4ac)/2a
AND,
x2 = (-b – √b2 – 4ac)/2a
The above two values of x are known as roots of the quadratic equation. The roots of a quadratic equation depend on the nature of the discriminant. The discriminant is part of the quadratic formula in the form of b 2 – 4 ac. A quadratic equation has two different real roots of the discriminant.
When the discriminant value is zero, then the equation will have only one root or solution. And, if the discriminant is negative, then the quadratic equation has no real root.
How to Solve Quadratic Equations?
Let’s solve a few examples of problems using the quadratic formula.
Example 1
Use the quadratic formula to find the roots of x2-5x+6 = 0.
Solution
Comparing the equation with the general form ax2 + bx + c = 0 gives,
a = 1, b = -5 and c = 6
b2 – 4ac = (-5)2 – 4×1×6 = 1
Substitute the values in the quadratic formula
x1 = (-b + √b2-4ac)/2a
⇒ (5 + 1)/2
= 3
x2 = (-b – √b2-4ac)/2a
⇒ (5 – 1)/2
= 2
Example 2
Solve the quadratic equation below using quadratic formula:
3x2 + 6x + 2 = 0
Solution
Comparing the problem with the general form of quadratic equation ax2 + bx + c = 0 gives,
a = 3, b = 6 and c = 2
x = [- b ± √ (b2– 4ac)]/2a
⇒ [- 6 ± √ (62 – 4* 3* 2)]/2*3
⇒ [- 6 ± √ (36- 24)]/6
⇒ [- 6 ± √ (12)]/6
x1 = (-6 + 2√3)/6
⇒ -(2/3) √3
x2 = (-6– 2√3)/6
⇒ -(4/3) √3
Example 3
Solve 5x2 + 6x + 1 = 0
Solution
Comparing with the quadratic equation, we get,
a = 5, b = 6, c = 1
Now apply the quadratic formula:
x = −b ± √ (b2 − 4ac)2a
Substitute the values of a, b and c
⇒ x = −6 ± √ (62 − 4×5×1)2×5
⇒ x = −6 ± √ (36 − 20)10
⇒ x = −6 ± √ (16)10
⇒ x = −6 ± 410
⇒ x = − 0.2, −1
Example 4
Solve 5x2 + 2x + 1 = 0
Solution
The coefficients are;
a = 5, b = 2, c = 1
In this case, the discriminant is negative:
b2 − 4ac = 22 − 4×5×1
= −16
Now apply the quadratic formula;
x = (−2 ± √ −16)/10
⇒√ (−16) = 4
Where i is the imaginary number √−1
⇒x = (−2 ± 4i)/10
Therefore, x = −0.2 ± 0.4i
Example 5
Solve x2 − 4x + 6.25 = 0
Solution
According to the standard form of a quadratic equation ax2 + bx + c = 0, we can observe that;
a = 1, b = −4, c = 6.25
Determine the discriminants.
b2 − 4ac = (−4)2 – 4 × 1 × 6.25
= −9 ………………. (negative discriminant)
⇒ x = −(−4) ± √ (−9)/2
⇒ √ (−9) = 3i; where i is the imaginary number √−1
⇒ x = (4 ± 3i)/2
Hence, x = 2 ± 1.5i
How to Graph a Quadratic Equation?
To graph a quadratic equation, here are the steps to follow:
- Given a quadratic equation, rewrite the equation by equating it to y or f(x)
- Choose arbitrary values of x and y to plot the curve
- Now graph the function.
- Read the roots where the curve crosses or touches the x-axis.
Solving quadratic equations by graphing
Graphing is another method of solving quadratic equations. The solution of the equation is obtained by reading the x-intercepts of the graph.
There are three possibilities when solving quadratic equations by graphical method:
- An equation has one root or solution if the x-intercept of the graph is 1.
- An equation with two roots has 2 x -intercepts
- If there is no x – intercepts, then an equation has no real solutions.
Let’s graph a few examples of quadratic equations. In these examples, we have drawn our graphs using graphing software, but for you to understand this lesson very well, draw your graphs manually.
Example 1
Solve the equation x2 + x – 3 = 0 by graphical method
Solution
Our arbitrary values are shown in the table below:
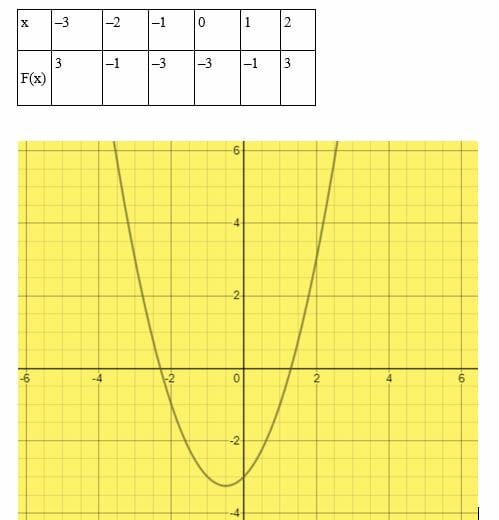
The x- intercepts are x = 1.3 and x = –2.3. Therefore, the roots of the quadratic equation are x = 1.3 and x = –2.3
Example 2
Solve the equation 6x – 9 – x2 = 0.
Solution
Choose arbitrary values of x.
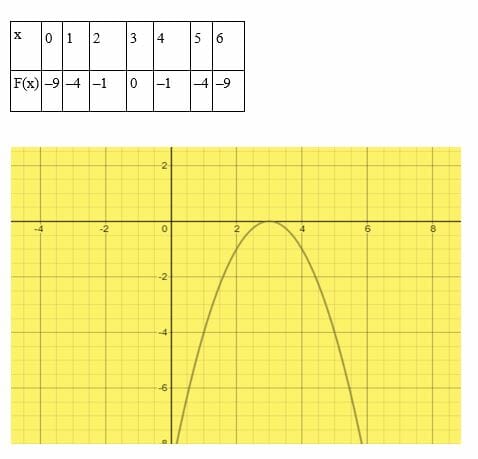
The curve touches the x-axis at x = 3. Therefore, 6x – 9 – x2 = 0 has one solution(x = 3).
Example 3
Solve the equation x2 + 4x + 8 = 0 by graphical method.
Solution
Choose arbitrary values of x.
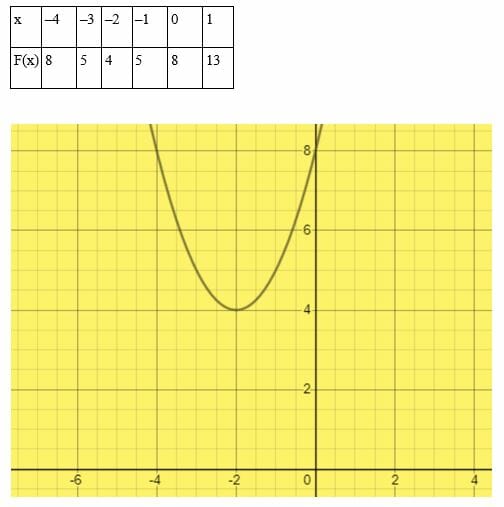
In this example, the curve does not touch or cross the x -axis. Therefore, the quadratic equation x2 + 4x + 8 = 0 does not have any real roots.
