Relations and Functions – Explanation & Examples
Functions and relations are one the most important topics in Algebra. On most occasions, many people tend to confuse the meaning of these two terms.
In this article, we will define and elaborate on how you can identify if a relation is a function. Before we go deeper, let’s look at a brief history of functions.
The concept of function was brought to light by mathematicians in the 17th century. In 1637, a mathematician and the first modern philosopher, Rene Descartes, talked about many mathematical relationships in his book Geometry. Still, the term “function” was officially first used by German mathematician Gottfried Wilhelm Leibniz after about fifty years. He invented a notation y = x to denote a function, dy/dx, to denote a function’s derivative. The notation y = f (x) was introduced by a Swiss mathematician Leonhard Euler in 1734.
Let’s now review some key concepts as used in functions and relations.
- What is a set?
A set is a collection of distinct or well-defined members or elements. In mathematics, members of a set are written within curly braces or brackets {}. Members of assets can be anything such as; numbers, people, or alphabetical letters, etc.
For example,
{a, b, c, …, x, y, z} is a set of alphabet letters.
{…, −4, −2, 0, 2, 4, …} is a set of even numbers.
{2, 3, 5, 7, 11, 13, 17, …} is a set of prime numbers
Two sets are said to be equal; they contain the same members. Consider two sets, A = {1, 2, 3} and B = {3, 1, 2}. Regardless of the members’ position in sets A and B, the two sets are equal because they contain similar members.
- What are ordered-pair numbers?
These are numbers that go hand in hand. Ordered pair numbers are represented within parentheses and separated by a comma. For example, (6, 8) is an ordered-pair number whereby the numbers 6 and 8 are the first and second elements, respectively.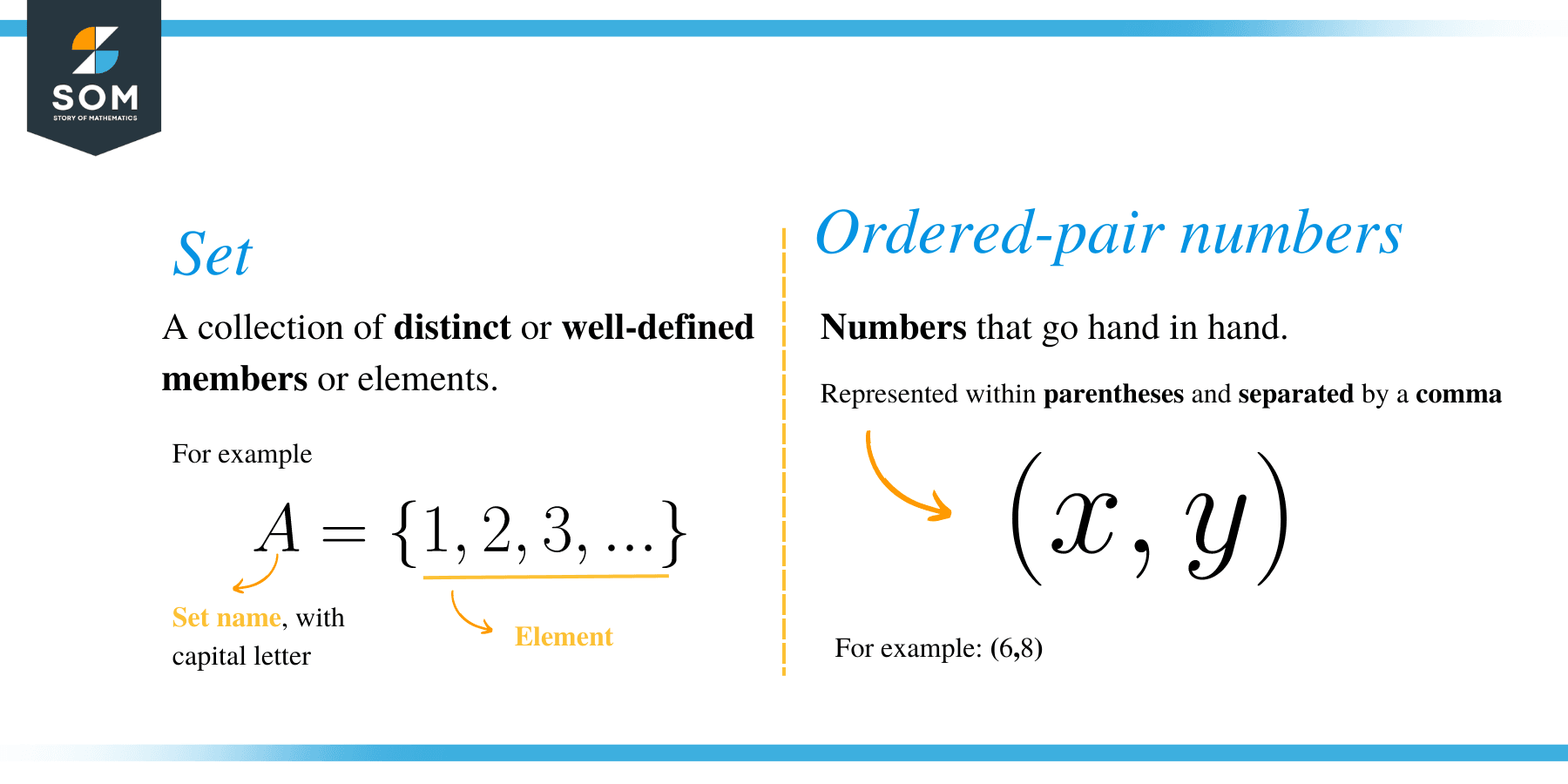
- What is a domain?
A domain is a set of all input or first values of a function. Input values are generally ‘x’ values of a function.
- What is a range?
The range of a function is a collection of all output or second values. Output values are ‘y’ values of a function.
- What is a function?
In mathematics, a function can be defined as a rule that relates every element in one set, called the domain, to exactly one element in another set, called the range. For example, y = x + 3 and y = x2 – 1 are functions because every x-value produces a different y-value.
- A relation
A relation is any set of ordered-pair numbers. In other words, we can define a relation as a bunch of ordered pairs.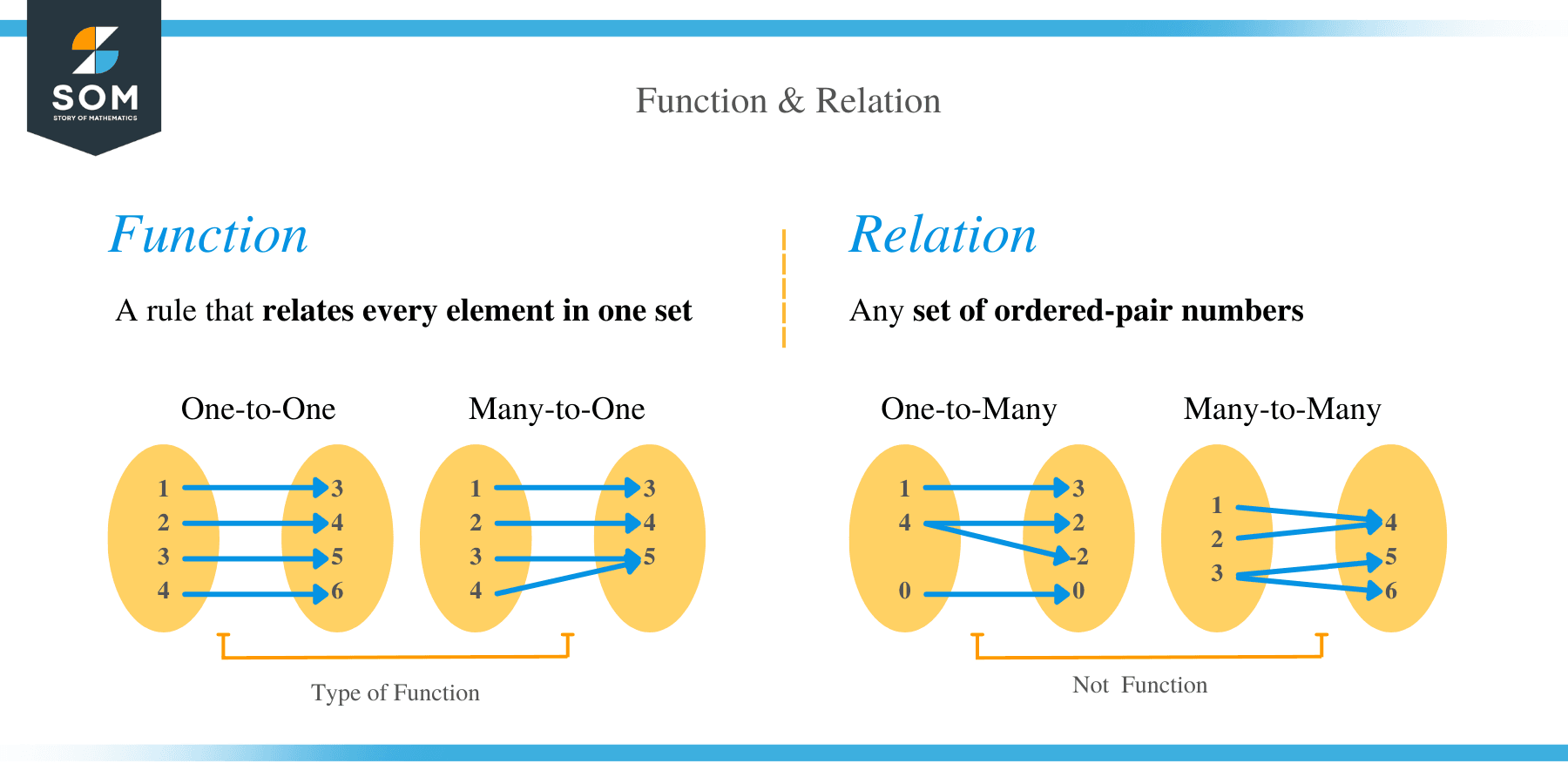
Types of Functions
Functions can be classified in terms of relations as follows:
- Injective or one-to-one function: The injective function f: P → Q implies that there is a distinct element of Q for each element of P.
- Many to one: The many to one function maps two or more P’s elements to the same element of set Q.
- The Surjective or onto function: This is a function for which every element of set Q there is a pre-image in set P
- Bijective function.
The common functions in algebra include:
- Linear Function
- Inverse Functions
- Constant Function
- Identity Function
- Absolute Value Function
How to Determine if a Relation is a Function?
We can check if a relation is a function either graphically or by following the steps below.
- Examine the x or input values.
- Examine also the y or output values.
- If all the input values are different, then the relation becomes a function, and if the values are repeated, the relation is not a function.
Note: if there is a repetition of the first members with an associated repetition of the second members, the relation becomes a function.
Example 1
Identify the range and domain the relation below:
{(-2, 3), {4, 5), (6, -5), (-2, 3)}
Solution
Since the x values are the domain, the answer is, therefore,
⟹ {-2, 4, 6}
The range is {-5, 3, 5}.
Example 2
Check whether the following relation is a function:
B = {(1, 5), (1, 5), (3, -8), (3, -8), (3, -8)}
Solution
B = {(1, 5), (1, 5), (3, -8), (3, -8), (3, -8)}
Though a relation is not classified as a function if there is a repetition of x – values, this problem is a bit tricky because x values are repeated with their corresponding y-values.
Example 3
Determine the domain and range of the following function: Z = {(1, 120), (2, 100), (3, 150), (4, 130)}.
Solution
Domain of z = {1, 2, 3, 4 and the range is {120, 100, 150, 130}
Example 4
Check if the following ordered pairs are functions:
- W= {(1, 2), (2, 3), (3, 4), (4, 5)
- Y = {(1, 6), (2, 5), (1, 9), (4, 3)}
Solution
- All the first values in W = {(1, 2), (2, 3), (3, 4), (4, 5)} are not repeated, therefore, this is a function.
- Y = {(1, 6), (2, 5), (1, 9), (4, 3)} is not a function because, the first value 1 has been repeated twice.
Example 5
Determine whether the following ordered pairs of numbers are a function.
R = (1,1); (2,2); (3,1); (4,2); (5,1); (6,7)
Solution
There is no repetition of x values in the given set of ordered pairs of numbers.
Therefore, R = (1,1); (2,2); (3,1); (4,2); (5,1); (6,7) is a function.
