Function Notation – Explanation & Examples

The concept of functions was developed in the seventeenth century when Rene Descartes used the idea to model mathematical relationships in his book Geometry. The term “function” was then introduced by Gottfried Wilhelm Leibniz fifty years later after publication of Geometry.

Later, Leonhard Euler formalized the usage of functions when he introduced the concept of function notation; y = f (x). It was until 1837 when Peter Dirichlet – a German mathematician gave the modern definition of a function.

What is a Function?

In mathematics, a function is a set of inputs with a single output in each case. Every function has a domain and range. The domain is the set of independent values of the variable x for a relation or a function is defined.  In simple words, the domain is a set of x-values that generate the real values of y when substituted in the function.

On the other hand, the range is a set of all possible values that a function can produce. The range of a function can be expressed in interval notation or inform of inequalities.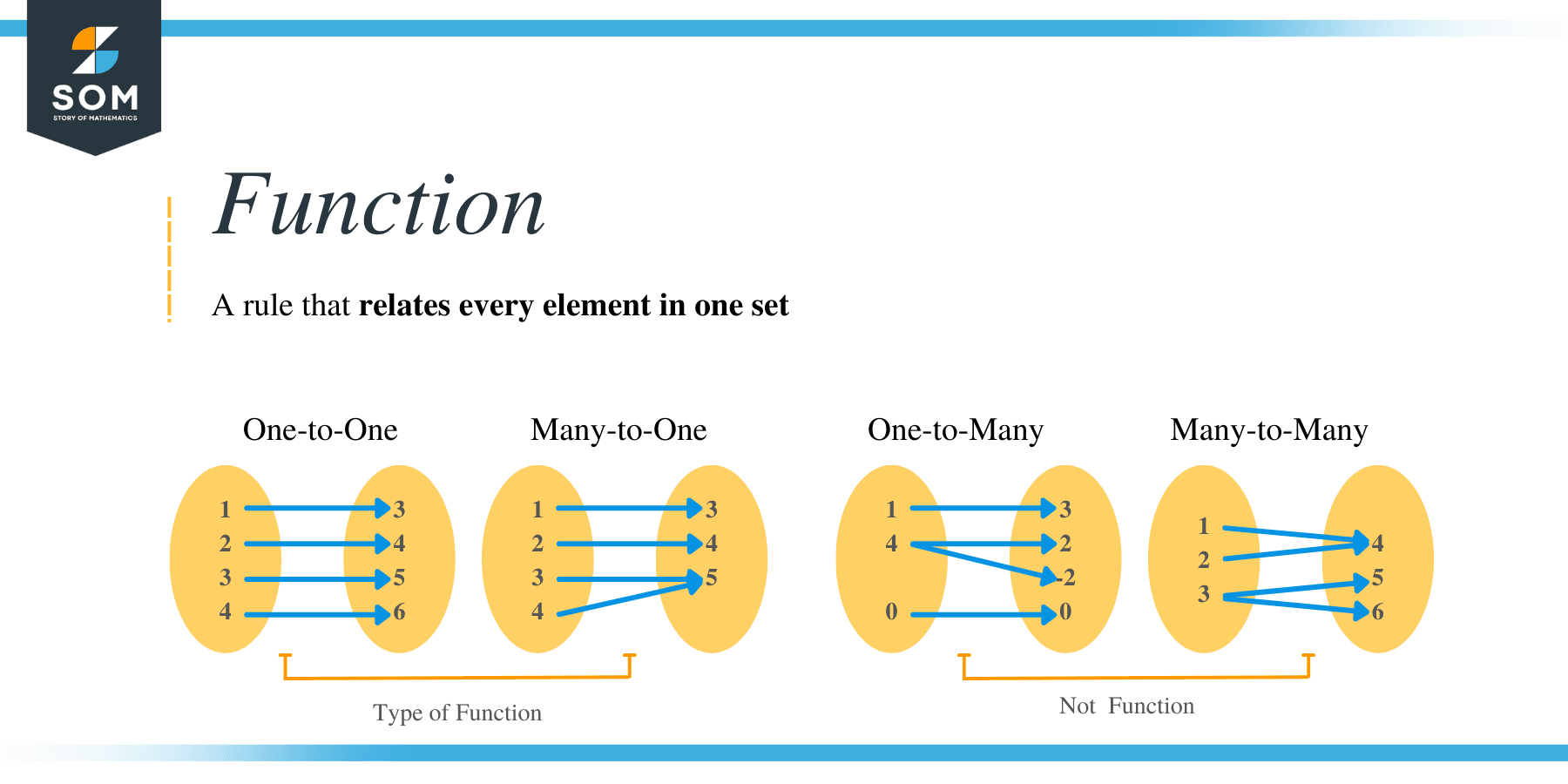

What is a Function Notation?

Notation can be defined as a system of symbols or signs that denote elements such as phrases, numbers, words etc.

Therefore, function notation is a way in which a function can be represented using symbols and signs. Function notation is a simpler method of describing a function without a lengthy written explanation.

The most frequently used function notation is f(x) which is read as “f” of “x”. In this case, the letter x, placed within the parentheses and the entire symbol f(x), stand for the domain set and range set respectively.

Although f is the most popular letter used when writing function notation, any other letter of the alphabet can also be used either in upper or lower case.

Advantages of using function notation

• Since most functions are represented with various variables such as; a, f, g, h, k etc., we use f(x) in order avoid confusion as to which function is being evaluated.
• Function notation allows to identify the independent variable with ease.
• Function notation also helps us to identify the element of a function which has to be examined.

Consider a linear function y = 3x + 7. To write such function in function notation, we simply replace the variable y with the phrase f(x) to get;

f(x) = 3x + 7. This function f(x) = 3x + 7 is read as the value of f at x or as f of x.

Types of functions

There are several types of functions in Algebra.

The most common types of functions include:

• Linear function

A linear function is a polynomial of first degree. A linear function has the general form of f(x) = ax + b, where a and b are numerical values and a ≠ 0.

• Quadratic function

A polynomial function of second degree is known as a quadratic function. The general form of a quadratic function is f(x) = ax² + bx + c, where a, b and c are integers and a ≠ 0.

• Cubic function

This is a polynomial function of 3^rd degree which is of the form f(x) = ax³ + bx² + cx + d

• Logarithmic function

A logarithmic function is an equation in which variable appears as an argument of a logarithm. The general of the function is f(x)=log a (x), where a is the base and x is the argument

• Exponential function

An exponential function is an equation in which the variable appears as an exponent. Exponential function is represented as f(x) = a^x.

• Trigonometric function

f(x) = sin x, f(x) = cos x etc. are examples of trigonometric functions

1. Identity Function:

An identity function is such that f: A→ B and f(x) = x, ∀ x ∈ A

1. Rational Function:

A function is said to be rational if R(x) = P(x)/Q(x), where Q(x) ≠ 0.

How to Evaluate Functions?

Function evaluation is the process of determining output values of a function. This is done by substituting the input values in the given function notation.

Example 1

Write y = x² + 4x + 1 using function notation and evaluate the function at x = 3.

Solution

Given, y = x² + 4x + 1

By applying function notation, we get

f(x) = x² + 4x + 1

Evaluation:

Substitute x with 3

f (3) = 3² + 4 × 3 + 1 = 9 + 12 + 1 = 22

Example 2

Evaluate the function f(x) = 3(2x+1) when x = 4.

Solution

Plug x = 4 in the function f(x).

f (4) = 3[2(4) + 1]

f (4) = 3[8 + 1]

f (4) = 3 x 9

f (4) = 27

Example 3

Write the function y = 2x² + 4x – 3 in function notation and find f (2a + 3).

Solution

y = 2x² + 4x – 3 ⟹ f (x) = 2x² + 4x – 3

Substitute x with (2a + 3).

f (2a + 3) = 2(2a + 3)² + 4(2a + 3) – 3

= 2(4a² + 12a + 9) + 8a + 12 – 3
= 8a² + 24a + 18 + 8a + 12 – 3
= 8a² + 32a + 27

Example 4

Represent y = x³ – 4x using function notation and solve for y at x = 2.

Solution

Given the function y = x³ – 4x, replace y with f(x) to get;

f(x) = x³ – 4x

Now evaluate f(x) when x = 2

⟹ f (2) = 2³ – 4 × 2 = 8 -8 = 0

Therefore, the value of y at x=2 is 0

Example 5

Find f (k + 2) given that, f(x) = x² + 3x + 5.

Solution

To evaluate f (k + 2), substitute x with (k + 2) in the function.

⟹ f (k + 2) = (k + 2) ² + 3(k + 2) + 5

⟹ k² + 2² + 2k (2) + 3k + 6 + 5

⟹ k² + 4 + 4k + 3k + 6 + 5

= k² + 7k + 15

Example 6

Given the function notation f (x) = x² – x – 4. Find the value of x when f (x) = 8

Solution

f (x) = x² – x – 4

Substitute f(x) by 8.

8 = x² – x – 4

x² – x – 12 = 0

Solve the quadratic equation by factoring to get;

⟹ (x – 4) (x + 3) = 0

⟹ x – 4 = 0; x + 3 = 0

Therefore, the values of x when f (x) = 8 are;

x = 4; x = -3

Example 7

Evaluate the function g(x) = x² + 2 at x = −3

Solution

Substitute x with -3.

g (−3) = (−3)² + 2 = 9 + 2 = 11

Real life examples of function notation

Function notation can be applied in real life to evaluate mathematical problems as shown in the following examples:

Example 8

To manufacture a certain product, a company spends x dollars on raw materials and y dollars on the labor. If the production cost is described by the function f (x, y) = 36000 + 40x + 30y + xy/100. Calculate cost of production when the firm spends $10,000 and $1,000 on raw materials and labor respectively.

Solution

Given x = $10,000 and y = $1,000

Substitute the values of x and y in the production cost function

⟹f (10000, 1000) = 36000 + 40(10000) + 30(1000) + (10000) (1000)/100.

⟹ f (10000, 1000) = 36000 + 4000000 + 30000 + 100000

⟹ $4136000.

Example 9

Mary is saving $100 weekly for her upcoming birthday party. If she already has $1000, how much will she have after 22 weeks?

Solution

Let x = number of weeks, and f(x) = total amount. We can write this problem in function notation as;

f(x)=100x + 1000
Now evaluate the function when x =22
f (22) =100(22) +1000
f (22) =3200

Therefore, the total amount is $3200.

Example 10

The rate of talk-time of two mobile networks A and B charges is $34 plus 0.05/min and $40 plus 0.04/min respectively.

1. Represent this problem in function notation.
2. Which mobile network is affordable given that average number of minutes used each month is 1,160.
3. When is the monthly bill of the two networks equal?

Solution

1. Let x be the number of minutes used in each network.

Therefore, the function of network A is f(x) = 0.05x + 34 and network B is f(x) = 0.04x+$40.

1. To determine which network is affordable, substitute x = 1160 in each function

A ⟹ f (1160) =0.05(1160) + 34

=58 + 34= $ 92

B ⟹ f (1160) = 0.04(1160) + 40

=46.4+40

= $ 86.4

Therefore, network B is affordable because its total talk-time cost is less than that of A.

1. Equate the two functions and solve x

⟹ 0.05x +34 = 0.04x + 40

⟹ 0.01x = 6

x = 600

The monthly bill of A and B will be equal when the average number of minutes is 600.

Proof:

A ⟹ 0.05(600) +34 = $64

B ⟹ 0.04(600) + 40 = $64

Example 11

A certain number is such that when its added to 142, the result is 64 more than thrice the original number. Find the number.

Solution

Let x = the original number and f(x) be the resultant number after adding 142.

f(x) = 142 + x = 3x + 64

2x = 78

x = 39

Example 12

If the product of two consecutive positive integers is 1122, find the two integers.

Solution

Let x be the first integer;

second integer = x + 1

Now form the function as;

f(x) = x (x + 1)

find the value of x if f(x) = 1122

Replace the function f(x) by 1122

1122 = x (x + 1)

1122 = x² + 1

x² = 1121

Find the square of both sides of the function

x = 33

x + 1 = 34

The integers are 33 and 34.