Domain and Range of a Function – Explanation & Examples

This article will explain the domain and range of a function mean and how to calculate the two quantities. Before getting into the topic of domain and range, let’s briefly describe what a function is.

In mathematics, we can compare a function to a machine that generates some output in correlation to a given input. By taking an example of a coin stamping machine, we can illustrate a function’s meaning as follows.

When you insert a coin into the coin stamping machine, the result is a stamped and flattened piece of metal. By considering a function, we can relate the coin and the flattened piece of metal with the domain and range. In this case, a function is considered to be the coin stamping machine.

Just like the coin stamping machine, which can only produce a single flattened piece of metal at a time, a function works in the same manner by giving out one result at a time.

History of a function

The idea of a function was introduced in the early seventeenth century when Rene Descartes (1596-1650) used the concept in his book Geometry (1637) to model mathematical problems.

Fifty years later, after the publication of Geometry, Gottfried Wilhelm Leibniz (1646-1716) introduced the term “function.” Later, Leonhard Euler (1707-1783) played a big role by introducing the technique of function notion, y = f (x).

Real-life application of a function

Functions are very useful in mathematics because they allow us to model real-life problems into a mathematical format.

Here are a few examples of the application of a function.

• Circumference of a circle

The circumference of a circle is a function of its diameter or radius. We can mathematically represent this statement as:

C(d) =dπ or C(r)=2π⋅r

• A shadow

The length of the shadow of an object is a function of its height.

• The position of a moving object

The location of a moving object such as a car is a function of time.

• Temperature

The temperature of a body is based on several factors and inputs.

• Money

The compound or simple interest is a function of the time, principal, and interest rate.

• Height of an object

The height of an object is a function of his/her age and body weight.

Having learned about a function now can proceed to how to calculate the domain and the range of a function.

What is the Domain and Range of a Function?

The domain of a function is the input numbers that, when plugged into a function, the result is defined. In simple words, we can define the domain of a function as the possible values of x that will make an equation true.

Some of the instances that will not make a valid function are when an equation is being divided by zero or a negative square root.

For example, f(x) = x² is a valid function because, no matter what value of x can be substituted into an equation, there is always a valid answer. For this reason, we can conclude that the domain of any function is all real numbers.

The range of a function is defined as a set of solutions to the equation for a given input. In other words, the range is the output or y value of a function. There is only one range for a given function.

How to use interval notations to specify Domain and Range?

Since the range and domain of a function are usually expressed in interval notation, it’s important to discuss the concept of interval notation.

The procedure for doing interval notation include:

• Write the numbers separated by a comma in ascending order.
• Enclose the numbers using parentheses () to show that an endpoint value is not included.
• Use brackets [] to enclose the numbers when the endpoint value is included.

How to Find the Domain and Range of a Function?

We can determine the domain of a function either algebraically or by the graphical method. To calculate the domain of a function algebraically, you solve the equation to determine the values of x.

Different types of functions have their own methods of determining their domain.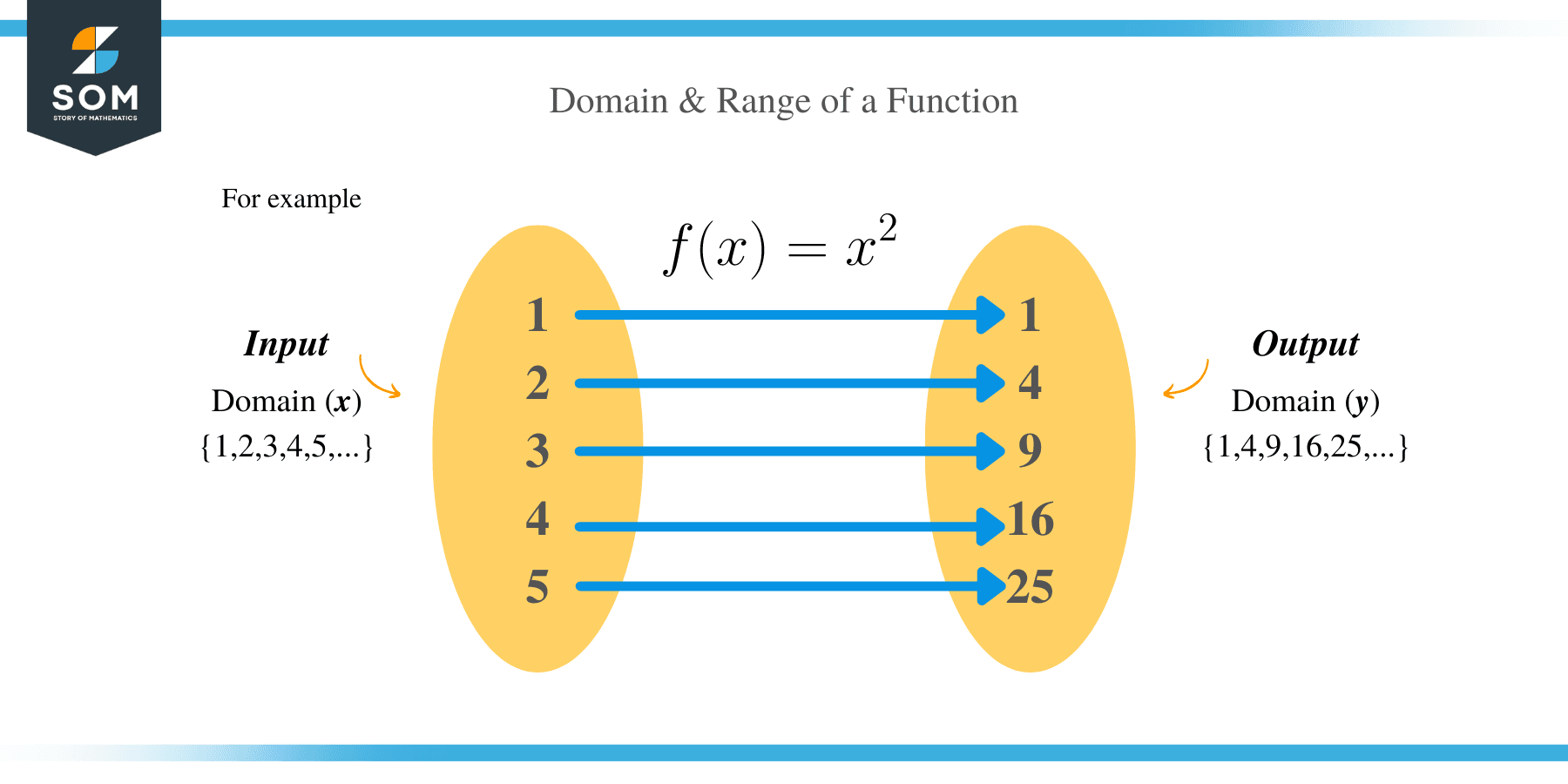

Let’s examine these types of functions and how to calculate their domain.

How to find the domain for a function with no denominator or radicals?

Let’s see a few examples below to understand this scenario.

Example 1

Find the domain of f (x) = 5x − 3

Solution

The domain of a linear function is all real numbers, therefore,

Domain: (−∞, ∞)

Range: (−∞, ∞)

A function with a radical

Example 2

Find the domain of the function f(x)=−2x² + 12x + 5

Solution

The function f(x) = −2x² + 12x + 5 is a quadratic polynomial, therefore, the domain is (−∞, ∞)

How to find the domain for a rational function with a variable in the denominator?

To find the domain of this type of function, set the denominator to zero and calculate the variable’s value.

Let’s see a few examples below to understand this scenario.

Example 3

Determine the domain of x−4/ (x² −2x−15)

Solution

Set the denominator to zero and solve for x

⟹ x² − 2x – 15 = (x − 5) (x + 3) = 0

Hence, x = −3, x = 5

For the denominator not to be zero, we need to avoid the numbers −3 and 5. Therefore, the domain is all real numbers except −3 and 5.

Example 4

Calculate the domain and the range of the function f(x) = -2/x.

Solution

Set the denominator to zero.

⟹ x = 0

Therefore, domain: All real numbers except 0.

The range is all real values of x except 0.

Example 5

Find the domain and range of the following function.

f(x) = 2/ (x + 1)

Solution

Set the denominator equal to zero and solve for x.

x + 1 = 0

= -1

Since the function is undefined when x = -1, the domain is all real numbers except -1. Similarly, the range is all real numbers except 0

How to the domain for a function with a variable inside a radical sign?

To find the domain of the function, the terms inside the radical are set the inequality of > 0 or ≥ 0. Then, the value of the variable is determined.

Let’s see a few examples below to understand this scenario.

Example 6

Find the domain of f(x) = √ (6 + x – x²)

Solution

To avoid the square roots of negative numbers, we set the expression inside the radical sign to ≥ 0.

6 + x – x² ≥ 0 ⟹ x ² – x – 6≤ 0

⟹ x ² – x – 6= (x – 3) (x +2) = 0

Therefore, the function is zero if x = 3 or x = -2

Hence the domain: [−2, 3]

Example 7

Find the domain of f(x) =x/√ (x² – 9)

Solution

Set the expression within the radical sign to x² – 9 > 0
Solve for the variable to get;

x = 3 or – 3

Therefore, Domain: (−∞, −3) & (3, ∞)

Example 8

Find the domain of f(x) = 1/√ (x² -4)

Solution

By factoring the denominator, we get x ≠ (2, – 2).

Test your answer by plugging -3 into the expression within the radical sign.

⟹ (-3)² – 4 = 5

also try with zero

⟹ 0² – 4 = -4, therefore number between 2 and -2 are invalid

Try number above 2

⟹ 3² – 4 = 5. This one is valid.

Hence, the domain = (-∞, -2) U (2, ∞)

How to find the domain of a function using the natural logarithm (ln)?

To find the domain of a function using natural log, set the terms within the parentheses to >0 and then solve.

Let’s see an example below to understand this scenario.

Example 9

Find the domain of the function f(x) = ln (x – 8)

Solution

⟹ x – 8 > 0

⟹ x – 8 + 8 > 0 + 8

⟹ x > 8

Domain:(8, ∞)

How to find the domain and range of a relation?

A relation is an asset of x and y coordinates. To find the domain and range in a relation, just list the x and y values, respectively.

Let’s see a few examples below to understand this scenario.

Example 10

State the domain and range of the relation {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}

Solution

List the x values. Domain: {2, 3, 4, 6}

List the y values. range: {–3, –1, 3, 6}

Example 11

Find the domain and range of the relation {(–3, 5), (–2, 5), (–1, 5), (0, 5), (1, 5), (2, 5)}

Solution

The domain is {–3, –2, –1, 0, 1, 2} and the range is {5}

Example 12

Given that R = {(4, 2) (4, -2), (9, 3) (9, -3)}, find the domain and range of R.

Solution

The domain is a list of first values, therefore, D= {4, 9} and the range = {2, -2, 3, -3}