Properties of Logarithm – Explanation & Examples

Before getting into the properties of logarithms, let’s briefly discuss the relationship between logarithms and exponents. The logarithm of a number is defined as t the power or index to which a given base must be raised to obtain the number.

Given that, a^x = M; where a and M is greater than zero and a ≠ 1, then, we can symbolically represent this in logarithmic form as;

log _a M = x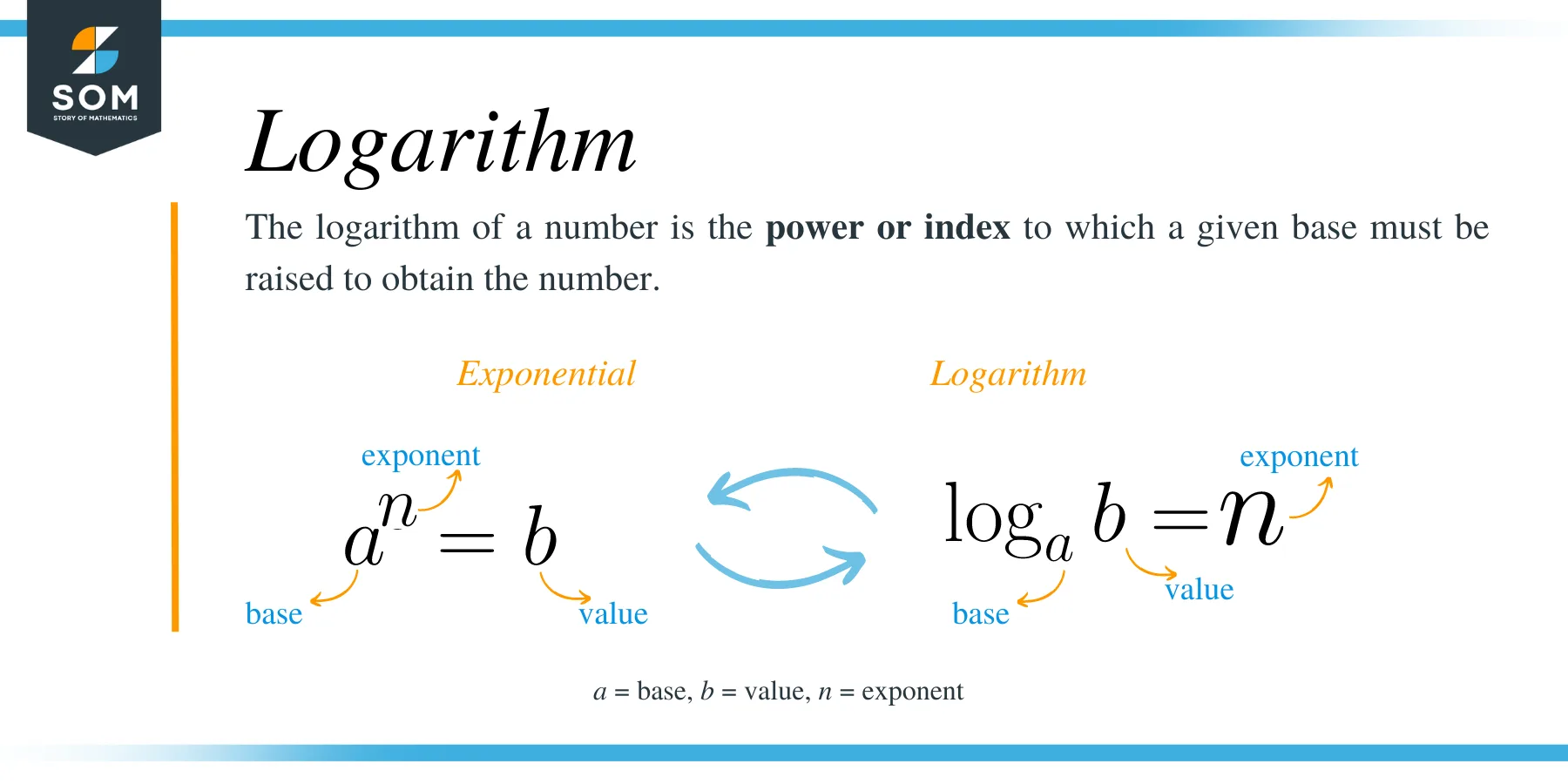

Examples:

• 2^-3= ¹/₈ ⇔ log ₂ (¹/₈) = -3
• 10^-2= 0.01 ⇔ log ₁₀01 = -2
• 2⁶= 64 ⇔ log ₂ 64 = 6
• 3²= 9 ⇔ log ₃ 9 = 2
• 5⁴= 625 ⇔ log ₅ 625 = 4
• 7⁰= 1 ⇔ log ₇ 1 = 0
• 3^{– 4}= 1/3⁴ = 1/81 ⇔ log ₃ 1/81 = -4
• 10^-2= 1/100 = 0.01 ⇔ log ₁₀01 = -2

Logarithmic Properties

Logarithm properties and rules are useful because they allow us to expand, condense or solve logarithmic equations. It for these reasons.

In most cases, you are told to memorize the rules when solving logarithmic problems, but how are these rules derived.

In this article, we will look at the properties and rules of logarithms derived using the laws of exponents.

• 

  Product property of logarithms

The product rule states that the multiplication of two or more logarithms with common bases is equal to adding the individual logarithms i.e.

log _a (MN) = log _a M + log _a N

Proof

• Let x = log _aM and y = log _a
• Convert each of these equations to the exponential form.

⇒ a ^x = M

⇒ a ^y = N

• Multiply the exponential terms (M & N):

a^x * a^y = MN

• Since the base is common, therefore, add the exponents:

a ^{x + y} = MN

• Taking log with base ‘a’ on both sides.

log _a (a ^{x + y}) = log _a (MN)

• Applying the power rule of a logarithm.

log _a Mⁿ ⇒ n log _a M

(x + y) log _a a = log _a (MN)

(x + y) = log _a (MN)

• Now, substitute the values of x and y in the equation we get above.

log _a M + log _a N = log _a (MN)

Hence, proved

log _a (MN) = log _a M + log _a N

Examples:

1. log50 + log 2 = log100 = 2
2. log ₂ ​ (4 x 8) ​ = log ₂ ​ (2² x 2³) =5

• Quotient property of logarithms

This rule states that the ratio of two logarithms with the same bases is equal to the difference of the logarithms i.e.

log _a (M/N) = log _a M – log _a N

Proof

• Let x = log _aM and y = log _a
• Convert each of these equation to the exponential form.

⇒ a ^x = M

⇒ a ^y = N

• Divide the exponential terms (M & N):

a^x / a^y = M/N

• Since the base is common, therefore, subtract the exponents:

a ^{x – y} = M/N

• Taking log with base ‘a’ on both sides.

log _a (a ^{x – y}) = log _a (M/N)

• Applying the power rule of logarithm on both sides.

log _a Mⁿ ⇒ n log _a M

(x – y) log _a a = log _a (M/N)

(x – y) = log _a (M/N)

• Now, substitute the values of x and y in the equation we get above.

log _a M – log _a N = log _a (M/N)

Hence, proved

log _a (M/N) = log _a M – log _a N

• Power property of logarithms

According to the power property of logarithm, the log of a number ‘M’ with exponent ‘n’ is equal to the product of exponent with a log of a number (without exponent) i.e.

log _a M ⁿ = n log _a M

Proof

• Let,

x = log _a M

• Rewrite as an exponential equation.

a ^x = M

• Take power ‘n’ on both sides of the equation.

(a ^x) ⁿ = M ⁿ

⇒ a ^xn = M ⁿ

• Take log on both sides of the equation with the base a.

log _a a ^xn = log _a M ⁿ

• log _a a ^xn = log _a M ⁿ ⇒ xn log _a a = log _a M ⁿ ⇒ xn = log _a M ⁿ

• Now, substitute the values of x and y in the equation we get above and simplify.

We know,

x = log _a M

So,

xn = log _a M ⁿ ⇒ n log _a M = log _a M ⁿ

Hence, proved

log _a M ⁿ = n log _a M

Examples:

log100³ = 3 log100 = 3 x 2 = 6

Change of base property of logarithms

According to the change of base property of logarithm, we can rewrite a given logarithm as the ratio of two logarithms with any new base. It is given as:

log _a M = log _b M/ log _b N

or

log _a M = log _b M × log _N b

Its proof can be done using one to one property and power rule for logarithms.

Proof

• Express each logarithm in exponential form by letting;

Let,

x = log _N M

• Convert it to exponential form,

M = N ^x

• Apply one to one property.

log _b N ^x = log _b M

• Applying the power rule.

x log _b N = log _b M

• Isolating x.

x = log _b M / log _b N

• Substituting the value of x.

log _a M = log _b M / log _b N

or we can write it as,

log _a M = log _b M × log _a b

Hence, proved.

Other properties of logarithms include:

• The logarithm of 1 to any finite non-zero base is zero.

Proof:

log _a 1 = 0⟹ a ⁰=1

• The logarithm of any positive number to the same base is equal to 1.

Proof:

log _a a=1 ⟹ a¹= a

Example:

log ₅ 15 = log 15/log 5