Finding Common Factors – Explanation & Examples

What is a Common Factor?

Before getting into common factors, let’s remind ourselves what factors are. Factors are whole numbers that are multiplied together to get another number. A factor of number divides the given number without leaving a remainder.

Every number has a factor that is less than or equal to the number itself. For example, the factors of the number 12 are 1, 2, 3, 4, 6, and 12 themselves. We can conclude that all numbers have a factor of 1, and every number is a factor of itself.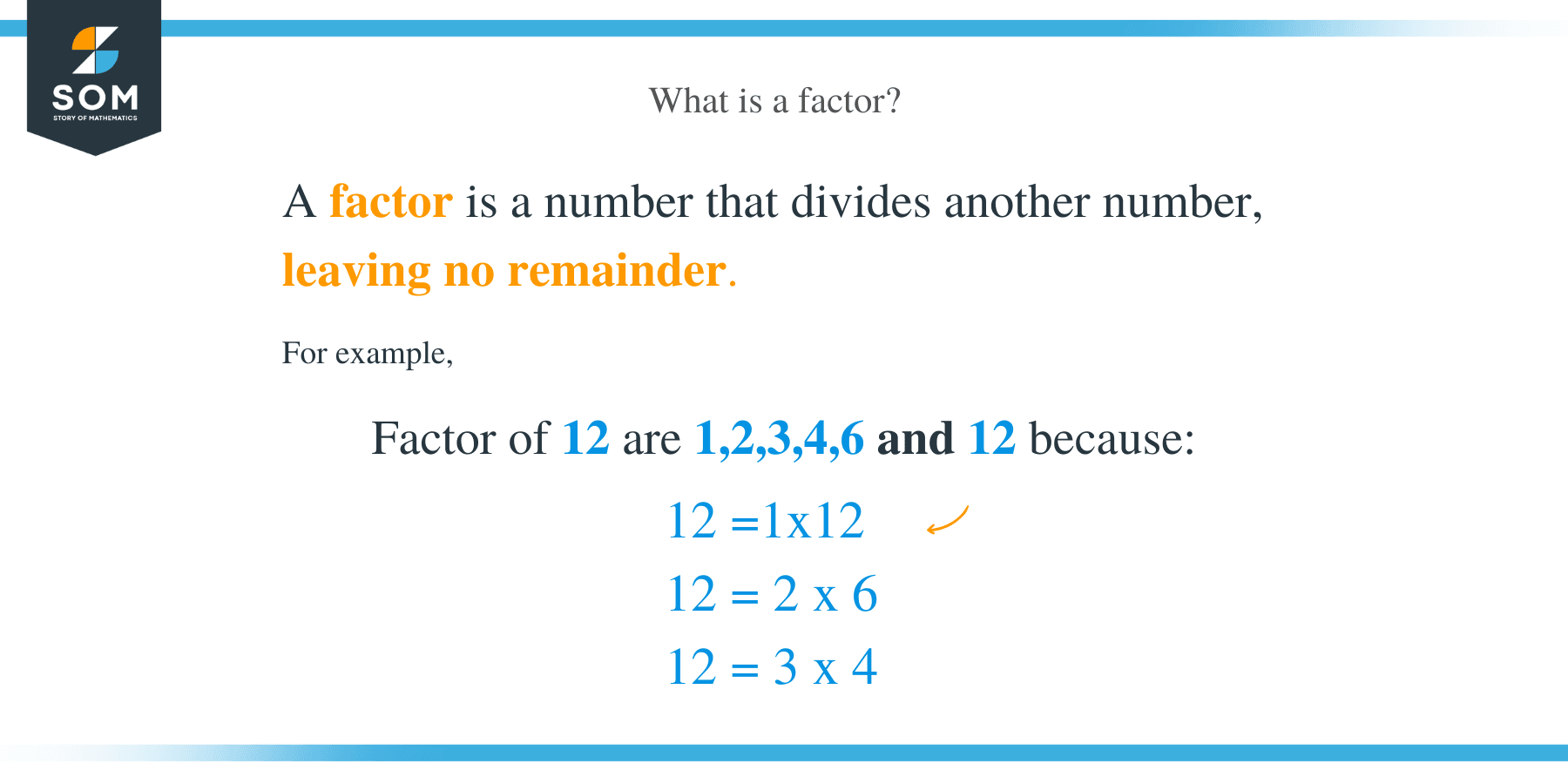

In mathematics, a common factor is defined as a number that can be divided into two or more different numbers without leaving a remainder.

How to Find Common Factors?

To find common factors of two or more numbers, the following procedure is undertaken:

• Separately write all the factors of each number.
• Identify the factors that are common to the numbers.
• You can perform this by encircling or drawing a line segment between the factors to stand out.
• The factors that these numbers share is what is referred to common factors

Let us solve a couple of examples here.

Example 1

Find the common factors of 20 and 36.

Solution

We need to list the factors of 20 and 36 separately;

Factors of 20 = 1, 2, 4, 5, 10 and 20.

Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, and 36.

Therefore, we can observe the common factors of 20 and 36 are 1, 2 and 4

Example 2

Determine the common factors of 18 and 48

Solution

Factors of 18 = 1, 2, 3, 6, 9, and 18.

Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.

Therefore, the common factors of 18 and 48 are 1, 2, 3, and 6.

Example 3

Find the common factors of 28, 45, and 80.

Solution

Factors of 28 = 1, 2, 4, 7, 14 and 28

Factors of 45 = 1, 3, 5, 9, 15 and 45

Factors of 80 = 1, 2, 4, 5, 8, 10, 16, 20, 40 and 80

We can clearly see that only the number 1 is common in the above lists. Therefore, 1 is the common factor in this case.

Example 4

What are the common factors of 36 and 63?

Solution

List down the factors of each number.

Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, and 36

Factors of 63 = 1, 3, 7, 9, 21 and 63

Since the numbers 1, 3, and 9 appear in both lists, these numbers are the common factors of 36 and 63.

Example 5

Find the common factors of the numbers 60, 90 and 150.
Solution

List the factors of each number;

60 = 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60.

90 = 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45 and 90.

150 = 1,2, 3, 5, 6, 10, 15, 25, 30, 50, 75 and 150.

From the above lists, we can conclude that the common factors of 60, 90 and 150 are1, 2, 3,5, 6,10, 15 and 30.

Example 6

Find the common factors of 70 and 315.

Solution

The factors of 70 are 1, 2, 5, 7, 10, 14, 35, and 70

Factors of the number 315 are 1, 3, 5, 7, 9, 15, 21, 35, 45, 63, 105, and 315.

Hence, 1,5, 7, and 35 are the common factors of 70 and 315.

Now that we learned how to find the common factors of different numbers, let’s see how we can apply them to solve mathematical problems. The skill of factoring numbers is essential in real-life situations such as simplifying fractions and comparing prices of commodities. Other application factors include understanding time, exchanging money and calculations, and dividing a quantity into equal amounts.