Solving Absolute Value Equations – Methods & Examples

What is Absolute Value?

Solving equations containing an absolute value is as simple as working with regular linear equations. Before we can embark on solving absolute value equations, let’s take a review of what the word absolute value means.

In mathematics, the absolute value of a number refers to the distance of a number from zero, regardless of direction. The absolute value of a number x is generally represented as | x | = a, which implies that, x = + a and -a.

We say that the absolute value of a given number is the positive version of that number. For example, the absolute value of negative 5 is positive 5, and this can be written as: | − 5 | = 5.

Other examples of absolute values of numbers include:  |− 9| = 9, |0| = 0, − |−12| = −12 etc. From these examples of absolute values, we simply define absolute value equations as equations containing expressions with absolute value functions.

How to Solve Absolute Value Equations?

The following are the general steps for solving equations containing absolute value functions:

• Isolate the expression containing the absolute value function.
• Get rid of the absolute value notation by setting up the two equations so that in the first equation, the quantity inside absolute notation is positive. In the second equation, it is negative. You will remove the absolute notation and write the quantity with its suitable sign.
• Calculate the unknown value for the positive version of the equation.
• Solve for the negative version of the equation, in which you will first multiply the value on the other side of the equal sign by -1, and then solve.

In addition to the above steps, there are other important rules you should keep in mind when solving absolute value equations.

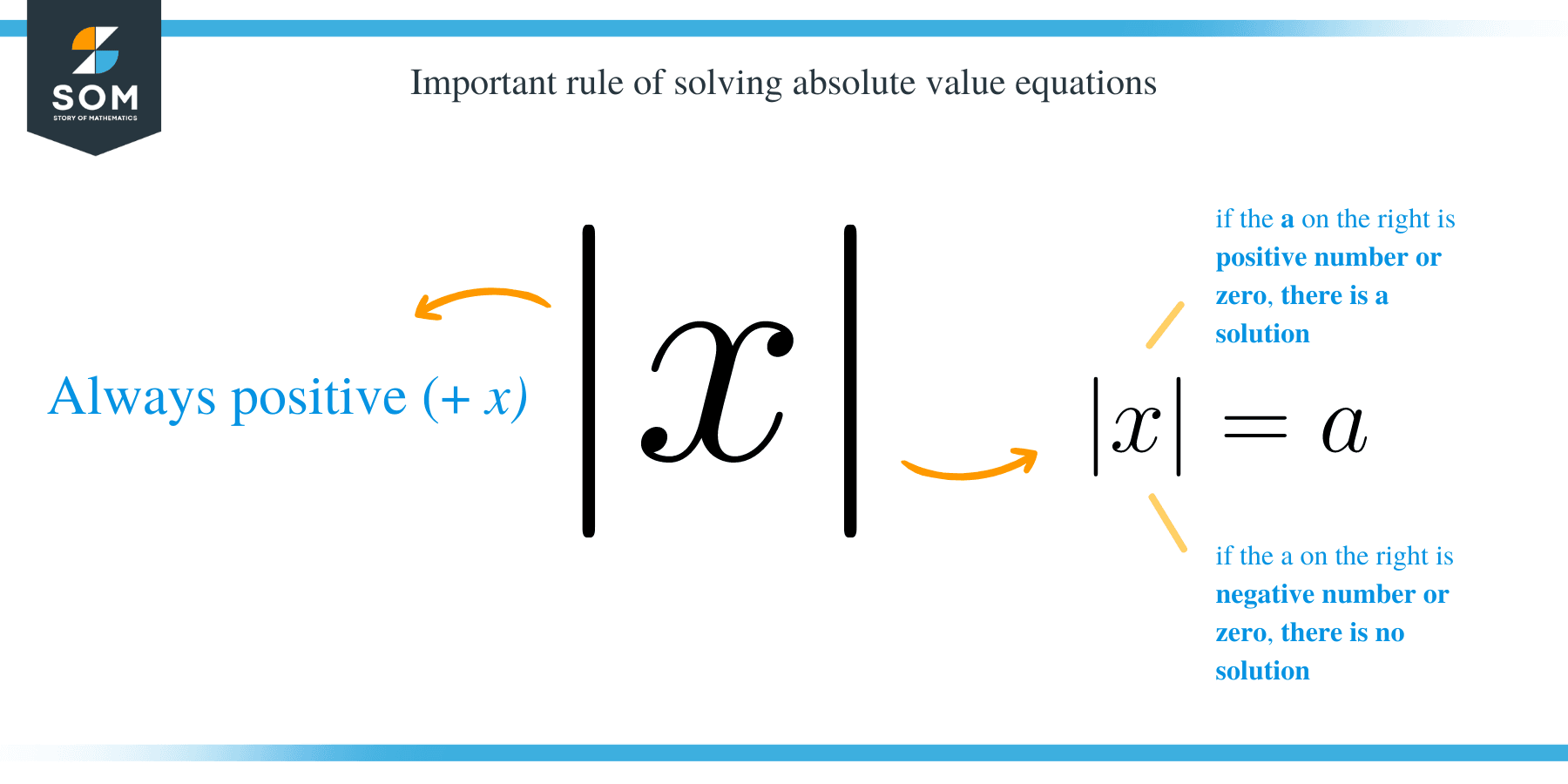
• The ∣x∣is always positive: ∣x∣ → +x.
• In | x| = a, if the a on the right is a positive number or zero, then there is a solution.
• In | x| = a, if the a on the right side is negative, there is no solution.

Example 1

Solve the equation for x: |3 + x| − 5 = 4.

Solution

• Isolate the absolute value expression by applying the Law of equations. This means, we add 5 to both sides of the equation to obtain;

| 3 + x | − 5 + 5 = 4 + 5

| 3 + x |= 9

• Calculate for the positive version of the equation. Solve the equation by assuming the absolute value symbols.

| 3 + x | = 9 → 3 + x = 9

Subtract 3 from both sides of the equation.

3 – 3 + x = 9 -3

x = 6

• Now calculate for the negative version of the equation by multiplying 9 by -1.

3 + x | = 9 → 3 + x = 9 × ( −1)

3 + x = -9

Also subtract 3 from both side to isolate x.

3 -3 + x = – 9 -3

x= -12

Therefore 6 and -12 are the solutions.

Example 2

Solve for all real values of x such that | 3x – 4 | – 2 = 3.

Solution

• Isolate the equation with absolute function by add 2 to both sides.

= | 3x – 4 | – 2 + 2 = 3 + 2

= | 3x – 4 |= 5

Assume the absolute signs and solve for the positive version of the equation.

| 3x – 4 |= 5→3x – 4 = 5

Add 4 to both sides of the equation.

3x – 4 + 4 = 5 + 4

3x = 9

Divide: 3x/3 =9/3

x = 3

Now solve for the negative version by multiplying 5 by -1.

3x – 4 = 5→3x – 4 = -1(5)

3x – 4 = -5

Add 4 to both sides of the equation.

3x – 4 + 4 = – 5 + 4

3x = 1

Divide by 3 on both sides.

3x/3 = 1/3

x = 1/3

Therefore, 3 and 1/3 are the solutions.

Example 3

Solve for all real values of x: Solve | 2x – 3 | – 4 = 3

Solution

Add 4 to both sides.

| 2x – 3 | -4 = 3 →| 2x – 3 | = 7

Assume the absolute symbols and solve for the positive version of x.

2x – 3 = 7

Add 3;

2x – 3 + 3 = 7 + 3

2x = 10

x = 5

Now solve for the negative version of x by multiplying 7 by -1

2x – 3 = 7→2x – 3 = -1(7)

2x -3 = -7

Add 3 to both sides.

2x – 3 + 3 = – 7 + 3

2x = -4

x = – 2

Therefore, x = –2, 5

Example 4

Solve for all real numbers of x: | x + 2 | = 7

Solution

Already the absolute value expression is isolated, therefore assume the absolute symbols and solve.

| x + 2 | = 7 → x + 2 = 7

Subtract 2 from both sides.

x + 2 – 2 = 7 -2

x = 5

Multiply 7 by -1 to solve for the negative version of the equation.

x + 2 = -1(7) → x + 2 = -7

Subtract by 2 on both sides.

x + 2 – 2 = – 7 – 2

x = -9

Therefore, x = -9, 5