Solving Cubic Equations – Methods & Examples
Solving higher order polynomial equations is an essential skill for anybody studying science and mathematics. However, understanding how to solve these kinds of equations is quite challenging.
This article will discuss how to solve the cubic equations using different methods such as the division method, Factor Theorem, and factoring by grouping.
But before getting into this topic, let’s discuss what a polynomial and cubic equation is.
A polynomial is an algebraic expression with one or more terms in which an addition or a subtraction sign separates a constant and a variable.
The general form of a polynomial is axn + bxn-1 + cxn-2 + …. + kx + l, where each variable has a constant accompanying it as its coefficient. The different types of polynomials include; binomials, trinomials and quadrinomial. Examples of polynomials are; 3x + 1, x2 + 5xy – ax – 2ay, 6x2 + 3x + 2x + 1 etc.
A cubic equation is an algebraic equation of third-degree.
The general form of a cubic function is: f (x) = ax3 + bx2 + cx1 + d. And the cubic equation has the form of ax3 + bx2 + cx + d = 0, where a, b and c are the coefficients and d is the constant.
How to Solve Cubic Equations?
The traditional way of solving a cubic equation is to reduce it to a quadratic equation and then solve it either by factoring or quadratic formula.
Like a quadratic equation has two real roots, a cubic equation may have possibly three real roots. But unlike a quadratic equation, which may have no real solution, a cubic equation has at least one real root.
The other two roots might be real or imaginary.
Whenever you are given a cubic equation or any equation, you always have to arrange it in a standard form first.
For example, if you are given something like this, 3x2 + x – 3 = 2/x, you will re-arrange into the standard form and write it like, 3x3 + x2 – 3x – 2 = 0. Then you can solve this by any suitable method.
Let’s see a few examples below for better understanding:
Example 1
Determine the roots of the cubic equation 2x3 + 3x2 – 11x – 6 = 0
Solution
Since d = 6, then the possible factors are 1, 2, 3 and 6.
Now apply the Factor Theorem to check the possible values by trial and error.
f (1) = 2 + 3 – 11 – 6 ≠ 0
f (–1) = –2 + 3 + 11 – 6 ≠ 0
f (2) = 16 + 12 – 22 – 6 = 0
Hence, x = 2 is the first root.
We can get the other roots of the equation using synthetic division method.
= (x – 2) (ax2 + bx + c)
= (x – 2) (2x2 + bx + 3)
= (x – 2) (2x2 + 7x + 3)
= (x – 2) (2x + 1) (x +3)
Therefore, the solutions are x = 2, x = -1/2 and x = -3.
Example 2
Find the roots of the cubic equation x3 − 6x2 + 11x – 6 = 0
Solution
x3 − 6x2 + 11x – 6
(x – 1) is one of the factors.
By dividing x3 − 6x2 + 11x – 6 by (x – 1),
⟹ (x – 1) (x2 – 5x + 6) = 0
⟹ (x – 1) (x – 2) (x – 3) = 0
This of the cubic equation solutions are x = 1, x = 2 and x = 3.
Example 3
Solve x3 – 2x2 – x + 2
Solution
Factorize the equation.
x3 – 2x2 – x + 2 = x2(x – 2) – (x – 2)
= (x2 – 1) (x – 2)
= (x + 1) (x – 1) (x – 2)
x = 1, -1 and 2.
Example 4
Solve the cubic equation x3 – 23x2 + 142x – 120
Solution
First factorize the polynomial.
x3 – 23x2 + 142x – 120 = (x – 1) (x2 – 22x + 120)
But x2 – 22x + 120 = x2 – 12x – 10x + 120
= x (x – 12) – 10(x – 12)
= (x – 12) (x – 10)
Therefore, x3 – 23x2 + 142x – 120 = (x – 1) (x – 10) (x – 12)
Equate each factor to zero.
x – 1= 0
x = 1
x – 10 = 10
x – 12= 0
x = 12
The roots of the equation are x = 1, 10 and 12.
Example 5
Solve the cubic equation x3 – 6 x2 + 11x – 6 = 0.
Solution
To solve this problem using division method, take any factor of the constant 6;
let x = 2
Divide the polynomial by x-2 to
(x2 – 4x + 3) = 0.
Now solve the quadratic equation (x2 – 4x + 3) = 0 to get x= 1 or x = 3
Therefore, the solutions are x = 2, x= 1 and x =3.
Example 6
Solve the cubic equation x3 – 7x2 + 4x + 12 = 0
Solution
Let f(x) = x3 – 7x2 + 4x + 12
Since d = 12, the possible values are 1, 2, 3, 4, 6 and 12.
By trial and error, we find that f (–1) = –1 – 7 – 4 + 12 = 0
So, (x + 1) is a factor of the function.
x3 – 7x2 + 4x + 12
= (x + 1) (x2 – 8x + 12)
= (x + 1) (x – 2) (x – 6)
Therefore x = –1, 2, 6
Example 7
Solve the following cubic equation:
x3 + 3x2 + x + 3 = 0.
Solution
x3 + 3x2 + x + 3
= (x3 + 3x2) + (x + 3)
= x2(x + 3) + 1(x + 3)
= (x + 3) (x2 + 1)
Therefore, x = -1 ,1 -3.
Example 8
Solve x3 − 6x2 + 11x − 6 = 0
Solution
Factorize
x3 − 6x2 + 11x − 6 = 0 ⟹ (x − 1) (x − 2) (x − 3) = 0
Equating each factor to zero gives;
x = 1, x = 2 and x = 3
Example 9
Solve x 3 − 4x2 − 9x + 36 = 0
Solution
Factorize each set of two terms.
x2(x − 4) − 9(x − 4) = 0
Extract the common factor (x − 4) to give
(x2 − 9) (x − 4) = 0
Now factorize the difference of two squares
(x + 3) (x − 3) (x − 4) = 0
By equating each factor to zero, we get;
x = −3, 3 or 4
Example 10
Solve the equation 3x3 −16x2 + 23x − 6 = 0
Solution
Divide 3x3 −16x2 + 23x – 6 by x -2 to get 3x2 – 1x – 9x + 3
= x (3x – 1) – 3(3x – 1)
= (x – 3) (3x – 1)
Therefore, 3x3 −16x2 + 23x − 6 = (x- 2) (x – 3) (3x – 1)
Equate each factor to zero to get,
x = 2, 3 and 1/3
Example 11
Find the roots of 3x3 – 3x2 – 90x=0
Solution
factor it out 3x
3x3 – 3x2 – 90x ⟹3x (x2 – x – 30)
Find a pair of factors whose product is −30 and sum is −1.
⟹- 6 * 5 =-30
⟹ −6 + 5 = -1
Rewrite the equation by replacing the term “bx” with the chosen factors.
⟹ 3x [(x2 – 6x) + (5x – 30)]
Factor the equation;
⟹ 3x [(x (x – 6) + 5(x – 6)]
= 3x (x – 6) (x + 5)
By equating each factor to zero, we get;
x = 0, 6, -5
Solving cubic equations using graphical method
If you cannot solve the cubic equation by any of the above methods, you can solve it graphically. For that, you need to have an accurate sketch of the given cubic equation.
The point(s) where its graph crosses the x-axis, is a solution of the equation. The number of real solutions of the cubic equations is same as the number of times its graph crosses the x-axis.
Example 12
Find the roots of x3 + 5x2 + 2x – 8 = 0 graphically.
Solution
Simply draw the graph of the following function by substituting random values of x:
f (x) = x3 + 5x2 + 2x – 8
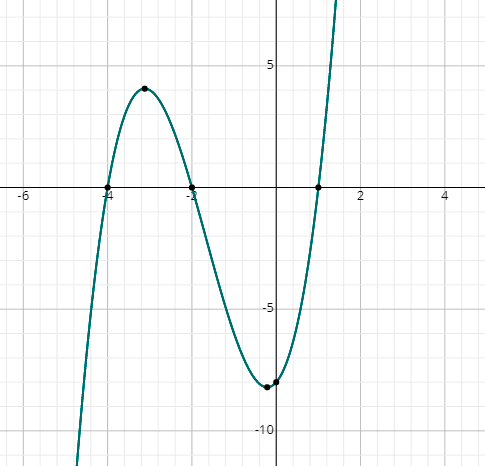
You can see the graph cuts the x-axis at 3 points, therefore, there are 3 real solutions.
From the graph, the solutions are:
x = 1, x = -2 & x = -4.
