Adding and Subtracting Expressions – Methods & Examples

Do you ever feel dazed when you hear about the addition and subtraction of rational numbers? If so, don’t worry, because this is your lucky day!

This article will lead you into a step-by-step tutorial on how to perform addition and subtraction of rational expressions, but before that, let’s remind ourselves what rational numbers are.

Rational number

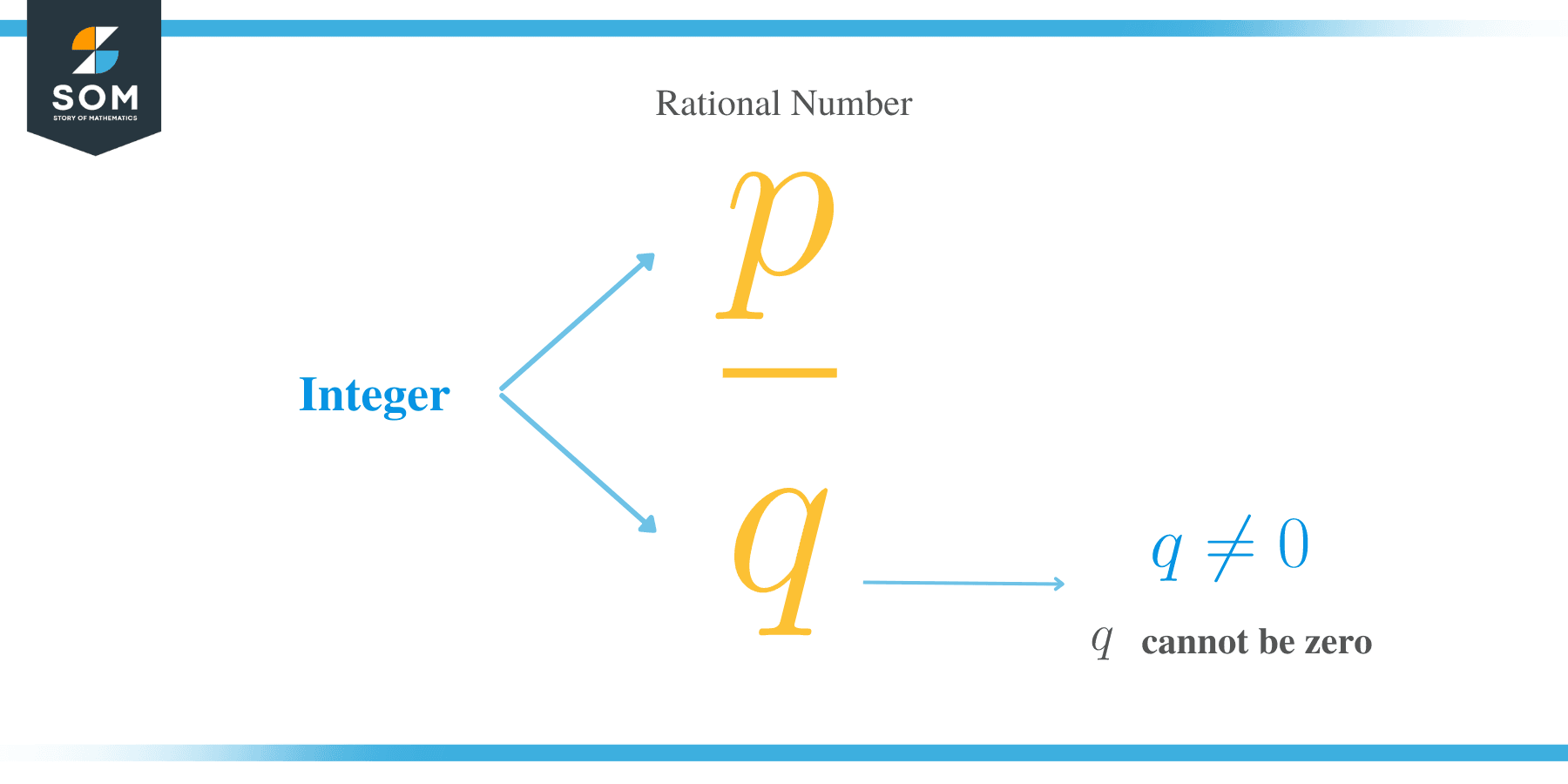
A rational number is a number that is expressed in the form of p/q, where ‘p’ and ‘q’ are integers and q ≠ 0.

In other words, a rational number is simply a fraction where the integer a is the numerator, and integer b is the denominator.

Example of rational numbers include: 2/3, 5/8, -3/14, -11/-5, 7/-9, 7/-15 and -6/-11 etc.

Algebraic expression

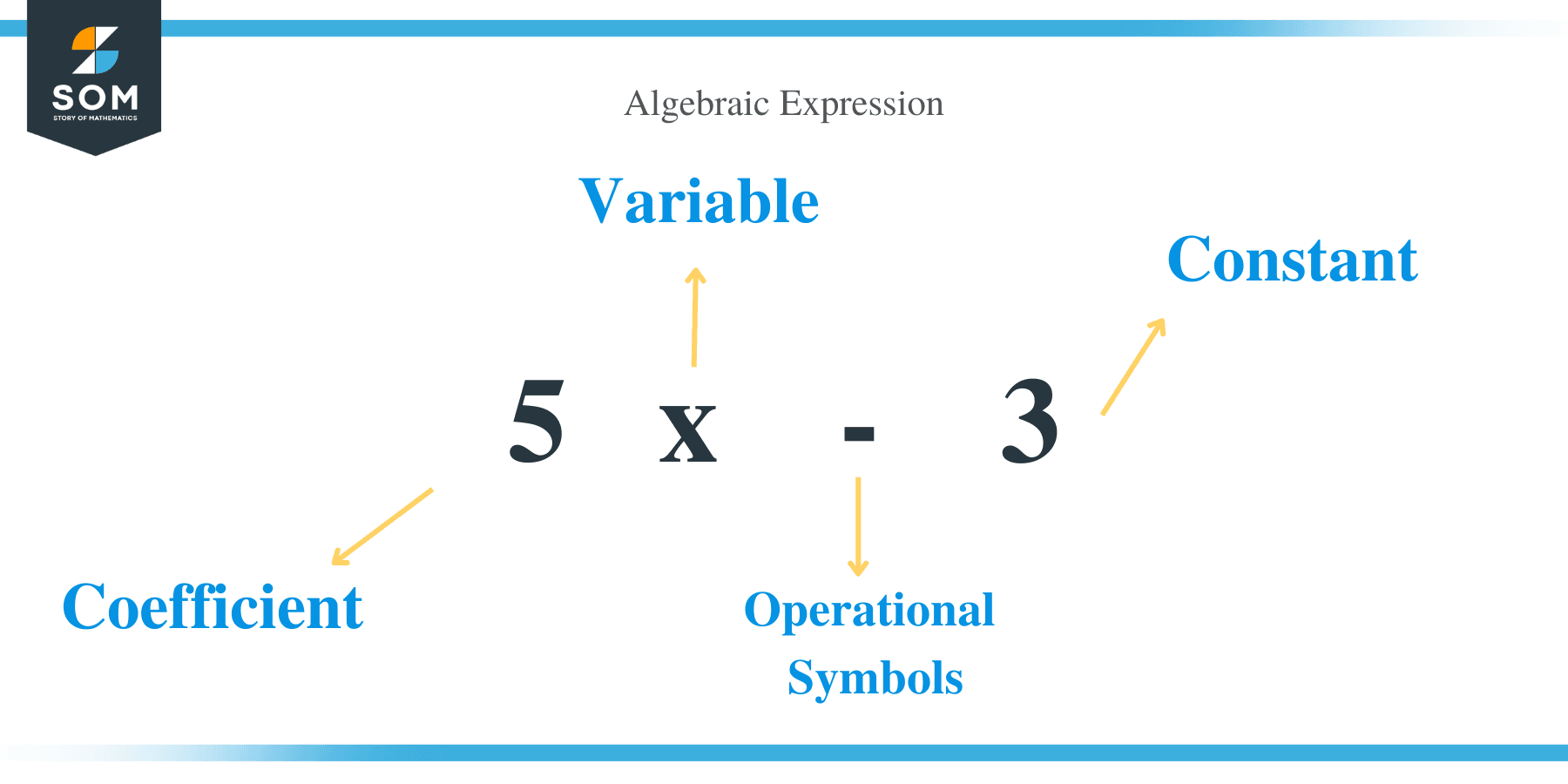
An algebraic expression is a mathematical phrase where variables and constants are combined using the operational (+, -, × & ÷) symbols. For example, 10x + 63 and 5x – 3 are examples of algebraic expressions.

Rational expression

We have learned that rational numbers are expressed in the form of p/q. On the other hand, a rational expression is a fraction in which either the denominator or the numerator is an algebraic expression. The numerator and the denominator are algebraic expressions. 

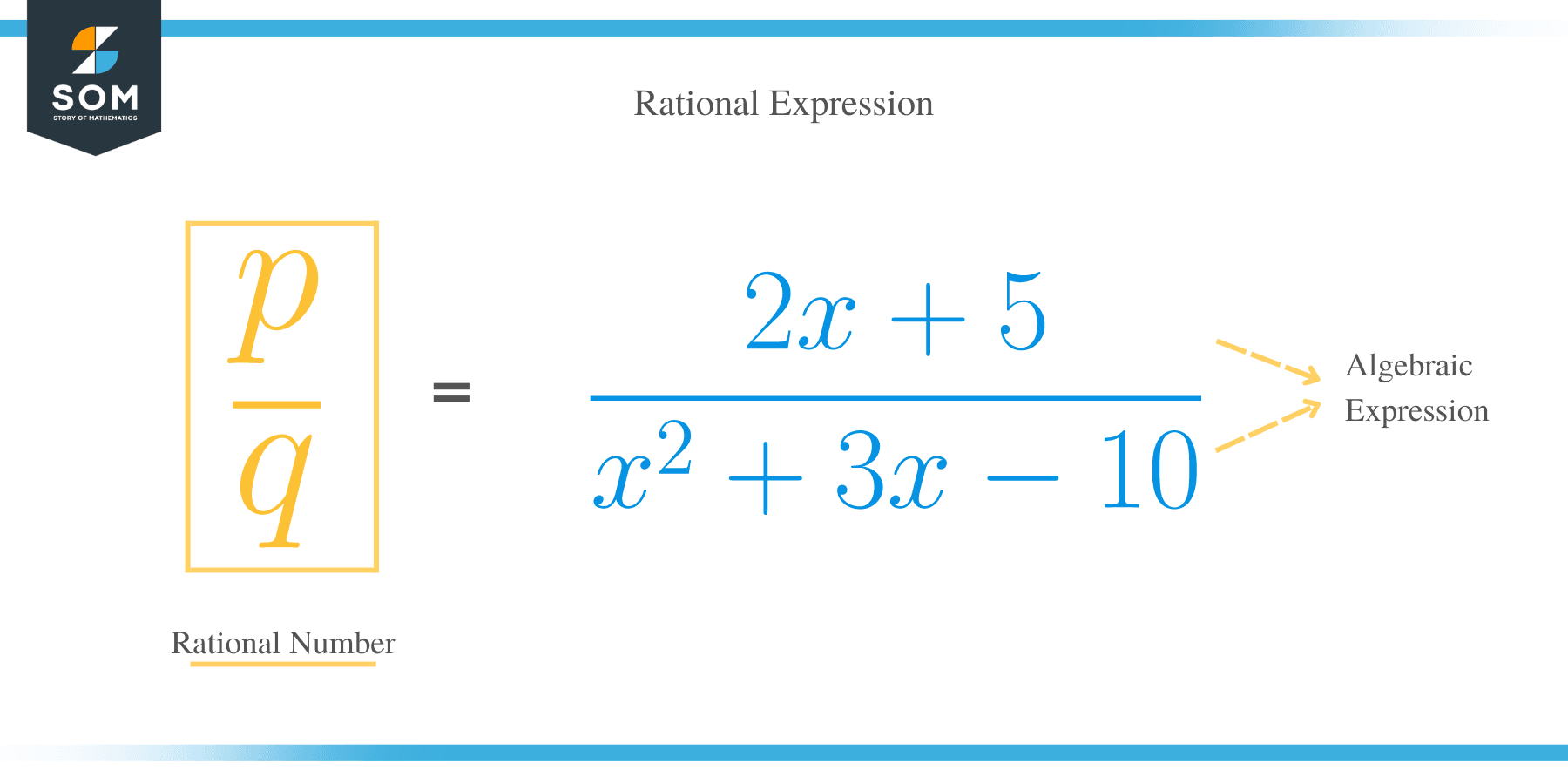
Examples of rational expression are:
3/ (x – 3), 2/ (x + 5), (4x – 1)/3, (x² + 7x)/6, (2x + 5)/(x² + 3x -10), (x+3)/(x + 6) etc.

How to Add Rational Expressions?

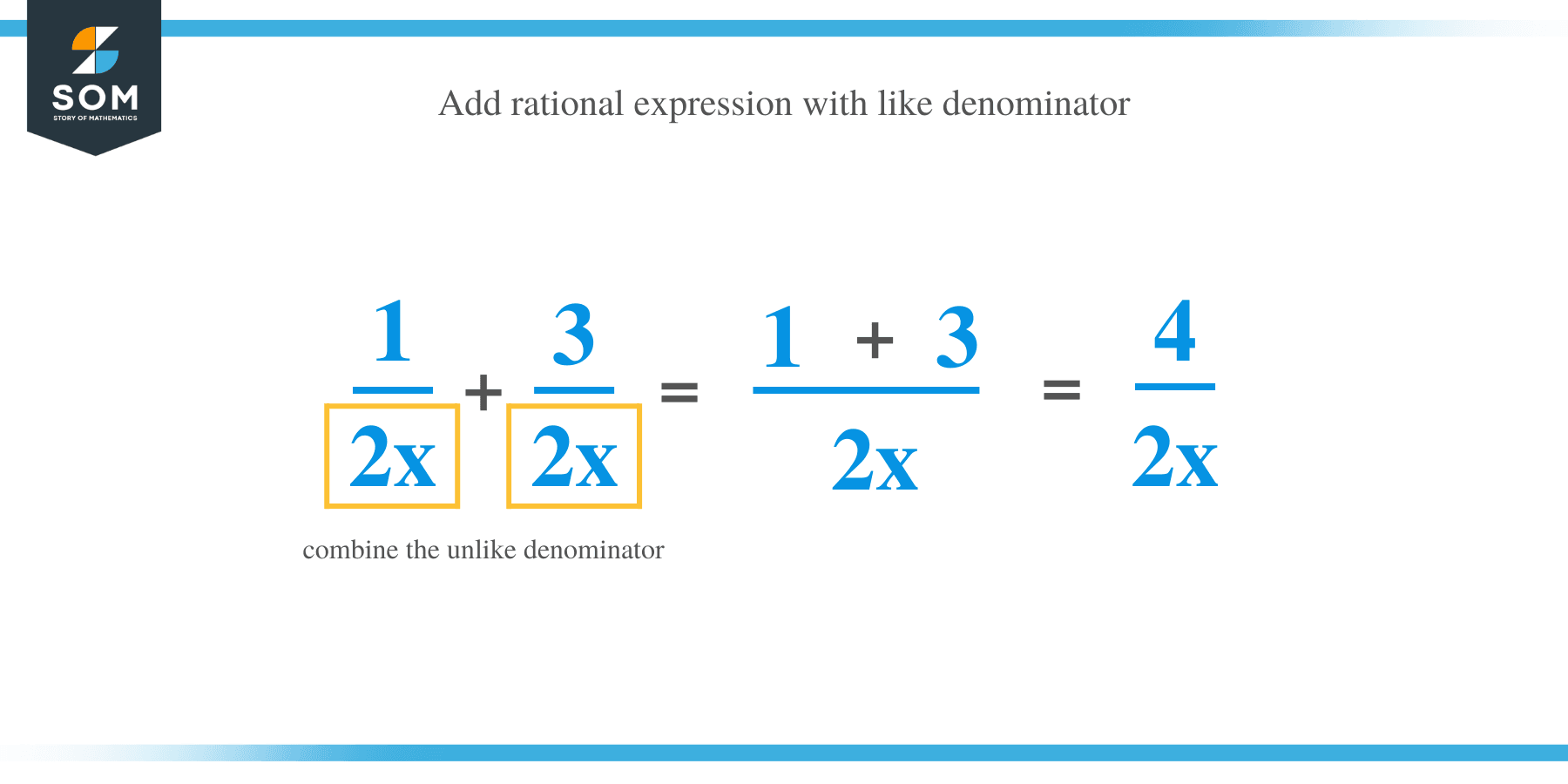
A rational expression with like denominators is added the same way as it is done with fractions. In this case, you keep the denominators and add the numerators together.

Example 1

Add (1/4x) + (3/4x)

Solution

Keep the denominators and add the numerators alone;

1/4x + 3/4x = (1 + 3)/4x

= 4/4x

Simplify the fraction to its lowest terms;

4/4x = 1/x

Example 2

Add (x + 6)/5 + (2x + 4)/5

Solution

Keeping the denominator, add the numerators;

(x + 6)/5 + (2x + 4)/5 = [(x + 6) + (2x + 4)]/5

= (x + 6 + 2x + 4)/5

Add the like terms and constants together;

= (x + 2x +6 + 4)5

= (3x + 10)/5

Example 3

Add 2/ (x + 7) + 8/ (x +7)

Solution

Keeping the denominator, add the numerators;

2/ (x + 7) + 8/ (x +7) = (2 + 8)/ (x + 7)

= 10/ (x + 7)

Adding rational expressions with unlike denominators

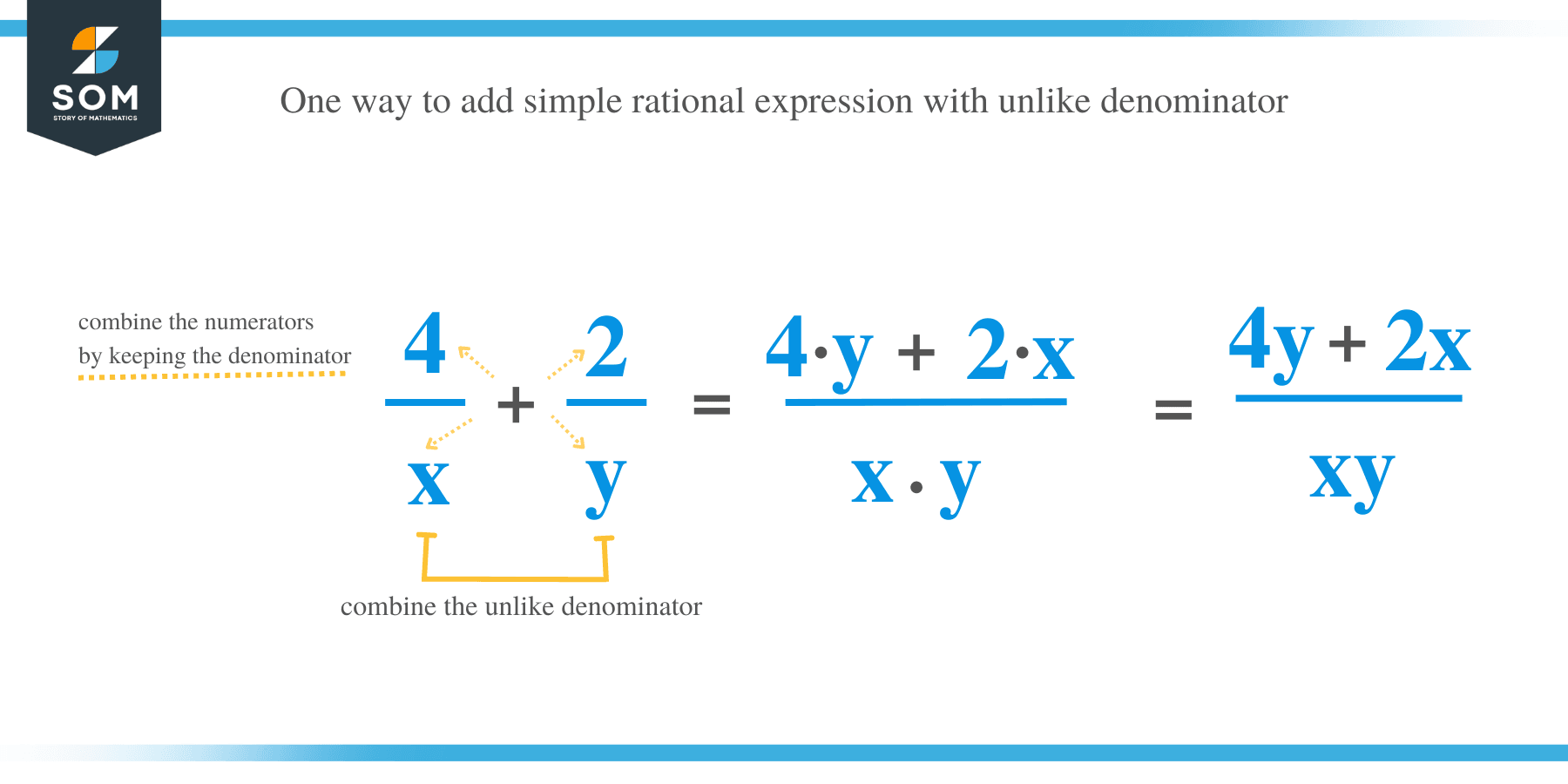
To add rational expression with different denominators, the following steps are followed:

• Factor out the denominator
• Determine the least common denominator (LCD). This is done by finding the product of different prime factors and the greatest exponent for each factor.
• Rewrite each rational expression with the LCD as the denominator by multiplying each fraction by 1
• Combine the numerators and keep the LCD as the denominator.
• Reduce the resultant rational expression if possible

Example 4

Add 6/x + 3/y

Solution

Find the LCD of the denominators. In this case, the LCD = xy.

Rewrite each fraction to contain the LCD as the denominator;

(6/x) (y/y) + (3/y) (x/x)

= 6y/xy + 3x /xy

Now combine the numerators by keeping the denominator;

6y/xy + 3x /xy = (6y +3x)/xy

The fraction cannot be simplified therefore, 6/x + 3/y = (6y +3x)/xy

Example 5

Add 4/ (x ² – 16) + 3/ (x ² + 8x + 16)

Solution

Start solving by factoring each denominator;

x ² – 16 = (x + 4) (x -4),

And x ² + 8x + 16 = (x +4) (x +4)

= (x + 4)²

4/ (x ² – 16) + 3/ (x ² + 8x + 16) = [4/ (x + 4) (x -4)] + 3/ (x + 4)²

Determine the LCD by finding the product of different prime factors and the greatest exponent for each factor. In this case, the LCD = (x – 4) (x + 4) ²

Rewrite each rational with the LCD as the denominator;

= [4/ (x + 4) (x -4)] (x + 4)/ (x + 4) + 3/ (x + 4)²(x – 4) (x -4)

= (4x + 16)/ [(x – 4) (x +4)²] + (3x – 12/ [(x- 4) (x +4)²]

By keeping the denominators, add the numerators;

= (4x +3x + 16 -12)/ [(x- 4) (x +4)²]

= (7x + 4)/ [(x- 4) (x +4)²]

Since the fraction can be simplified further, hence,

4/ (x ² – 16) + 3/ (x ² + 8x + 16) = (7x + 4)/ [(x- 4) (x +4)²]

How to Subtract Rational Expressions?

We can subtract rational expressions with like denominators by applying similar steps in addition.

Let’s take a look at some examples:

Example 6

Subtract 4/(x+1) – 1/ (x + 1)

Solution

Subtract the numerators by keeping the denominators;

Hence,

4/(x+1) – 1/ (x + 1) = (4- 1)/ / (x + 1)

= 3/x +1

Therefore, 4/(x+1) – 1/ (x + 1) =3/x +1

Example 7

Subtract :(4x – 1)/ (x – 3) – (1 + 3x)/ (x – 3).

Solution

Keeping the denominator constant, subtract the numerators;

(4x – 1)/ (x – 3) + (1 + 3x)/ (x – 3) = [(4x -1) – (1 + 3x)]/(x-3)

Open up the brackets;

= [4x -1 – 1 – 3x]/(x-3)              [ consider the PEMDAS]

= [4x – 3x – 1 -1]/x-3

= (x – 2)/ (x -3)

Example 8

Subtract (x² + 7x)/ (x – 7) – (10x + 28)/ (x – 7)

Solution

(x² + 7x)/ (x – 7) – (10x + 28)/ (x – 7) = (x ² + 7x – 10x -28)/(x-7)

= (x ² -3x – 28)/ (x -7)

Subtracting rational expression with unlike denominators

Let’s learn this using a few examples below.

Example 9

Subtract 2x / (x² – 9) – 1 / (x + 3)

Solution

Factor out the denominators;

x² – 9 = (x + 3) (x – 3).

Now rewrite,

2x / (x + 3) (x – 3) – 1 / (x + 3)

Find the lowest common denominator: LCD = (x + 3) (x – 3)/;

Multiply each fraction by the LCD;

2x – (x – 3) / (x + 3) (x – 3), which simplifies to x + 3 / x² – 9

Therefore,

2x / (x² – 9) – 1 / (x + 3) = x + 3 / x² – 9

Example 10

Subtract 2/a – 3/a – 5

Solution

Find the LCD;

The LCD = a(a−5).

Rewrite the fraction using the LCD;

2/a – 3/a – 5= 2(a – 5)/ [a (a – 5)] – 3a/[a(a−5)]

Subtract the numerators.

= (2a – 10 – 3a)/ [a(a−5)]

= -a -10/ a(a−5)