Multiplying Expressions – Methods & Examples

The operation of rational expressions might seem difficult to a few students, but the rules for multiplying expressions are just the same with integers. In Mathematics, a rational number is defined as a number in the form p/q, where p and q are integers and q is not equal to zero. 

Examples of rational numbers are: 2/3, 5/8, -3/14, -11/-5, 7/-9, 7/-15 and -6/-11 etc.

An algebraic expression is a mathematical phrase where variables and constants are combined using the operational (+, -, × & ÷) symbols.

For example, 10x + 63 and 5x – 3 are examples of algebraic expressions. Similarly, a rational expression is in the form p/q, and either or both p and q are algebraic expressions.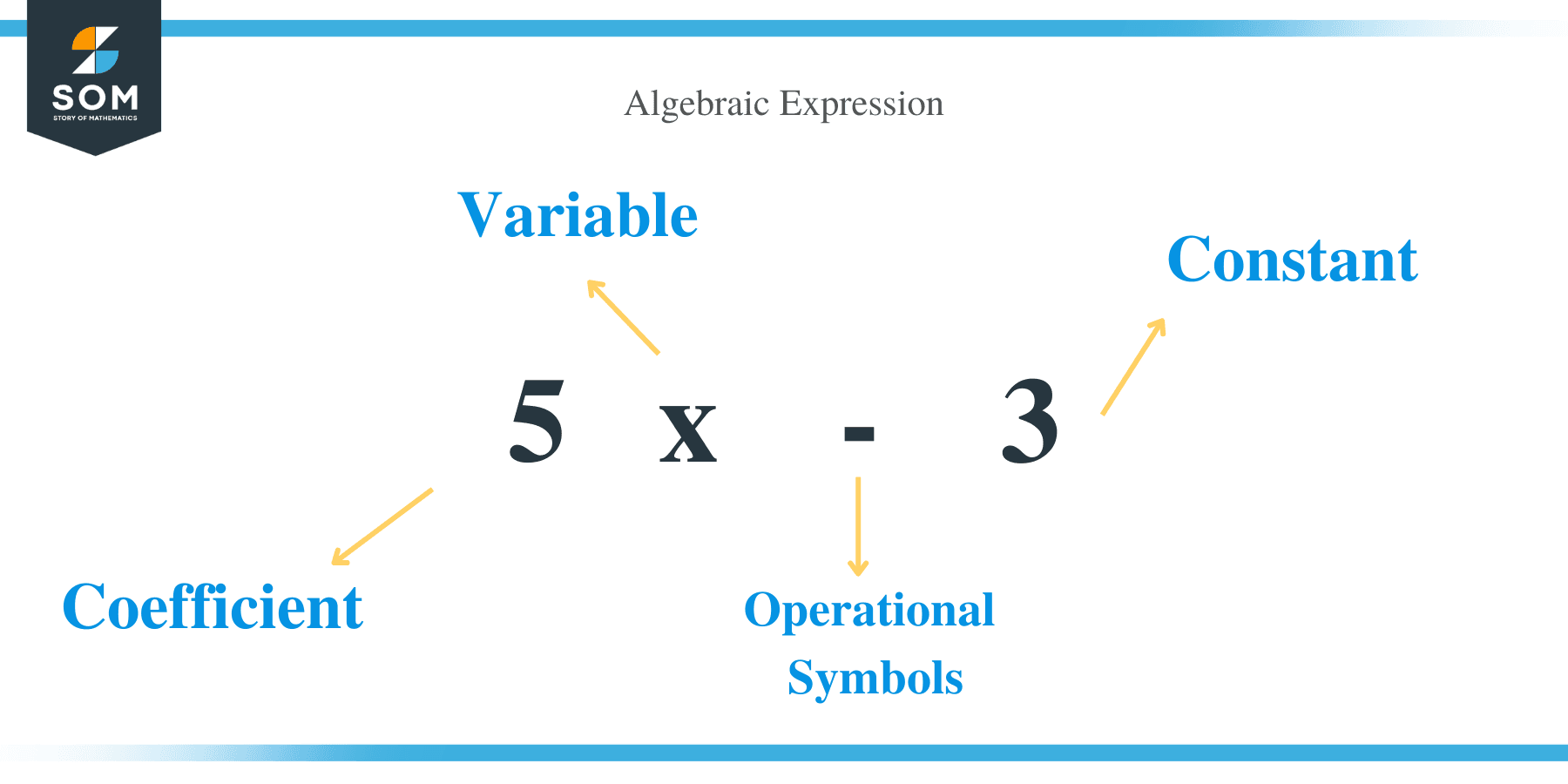

Examples of rational expression include: 3/ (x – 3), 2/ (x + 5), (4x – 1)/3, (x² + 7x)/6, (2x + 5)/ (x² + 3x – 10), (x + 3)/(x + 6) etc.

How to Multiply Rational Expressions?

In this article, we will learn how to multiply rational expressions, but before that, let us remind ourselves two fractions are multiplied.

Multiplication of two fractions entails finding the numerator of the first and the second fractions and the product of the denominator. In other words, the multiplication of two rational numbers is equal to the product of the numerators/product of their denominators.

Similarly, the multiplication of rational numbers is equal to the product of their numerators/product of their denominators. For instance, if a/b and c/d are two rational expressions, then multiplication of a/b by c/d is given by; a/b × c/d = (a × c)/ (b × d).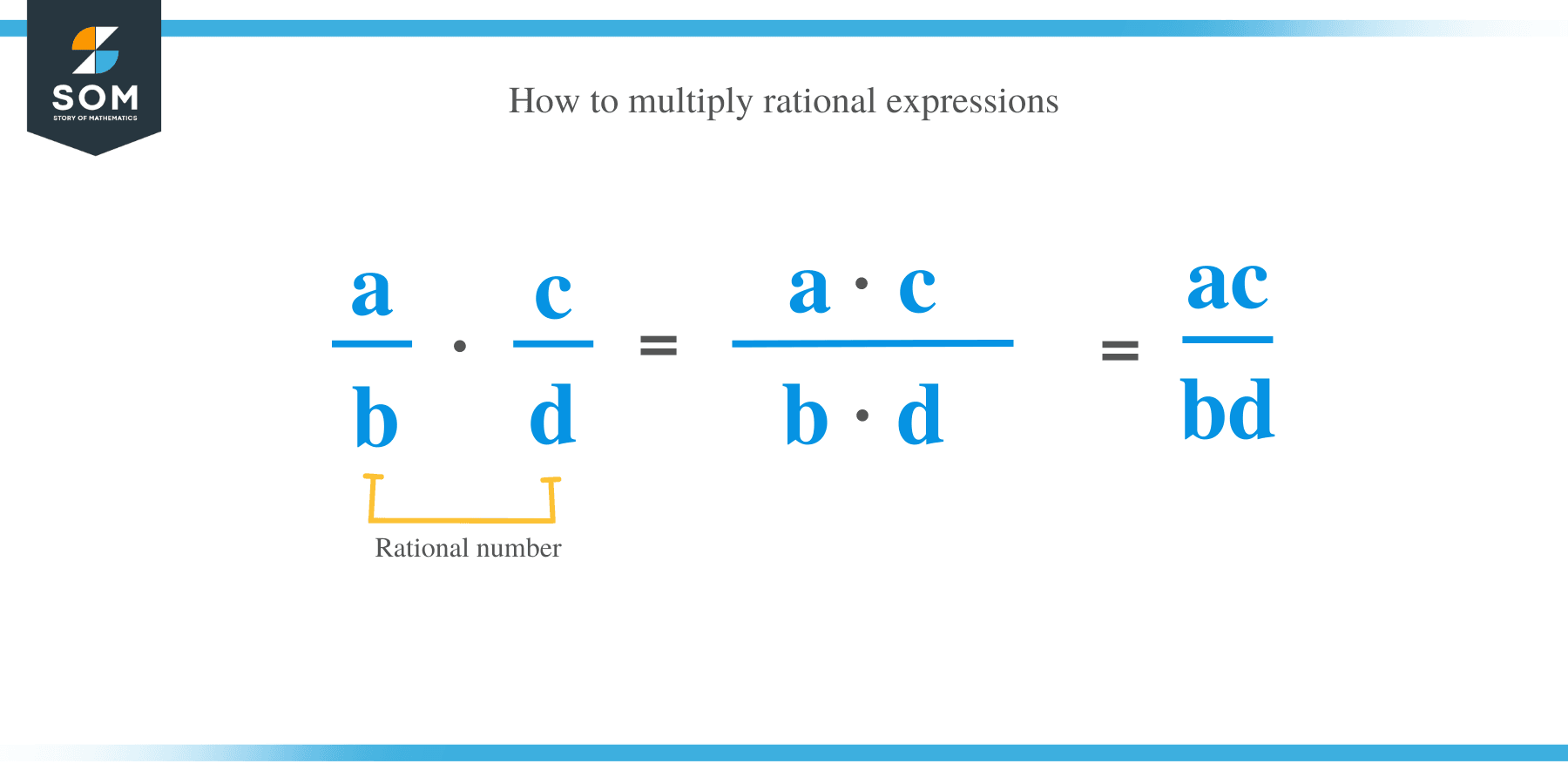

Alternatively, you can perform multiplication of rational expressions by; first factoring and canceling out the numerator and denominator and then multiplying the remaining factors.

Below are the steps required for multiplying rational expressions:

• Factor out both the denominator and numerator of each expression.
• Reduce the expressions to the lowest terms possible only if the numerators and denominators’ factors are common or similar.
• Multiply together the remaining expressions.

 

Example 1

Multiply 3/5y * 4/3y

Solution

Separately multiply the numerators and denominators;

3/5y * 4/3y = (3 * 4)/ (5y * 3y)

= 12/15y ²

Reduce the fraction by cancelling out by 3;

12/15y ² = 4/5y²

 

Example 2

Multiply {(12x – 4x ²)/ (x ² + x -12)} * {(x ² + 2x -8)/ (x ³-4x)}

Solution

Factor out both the numerators and denominators of each expression;

= {- 4x (x – 3)/(x-3) (x + 4)} * {(x – 2) (x + 4)/x (x + 2) (x – 2)}

Reduce or cancel the expressions and rewrite the remaining fraction;

= -4/ x + 2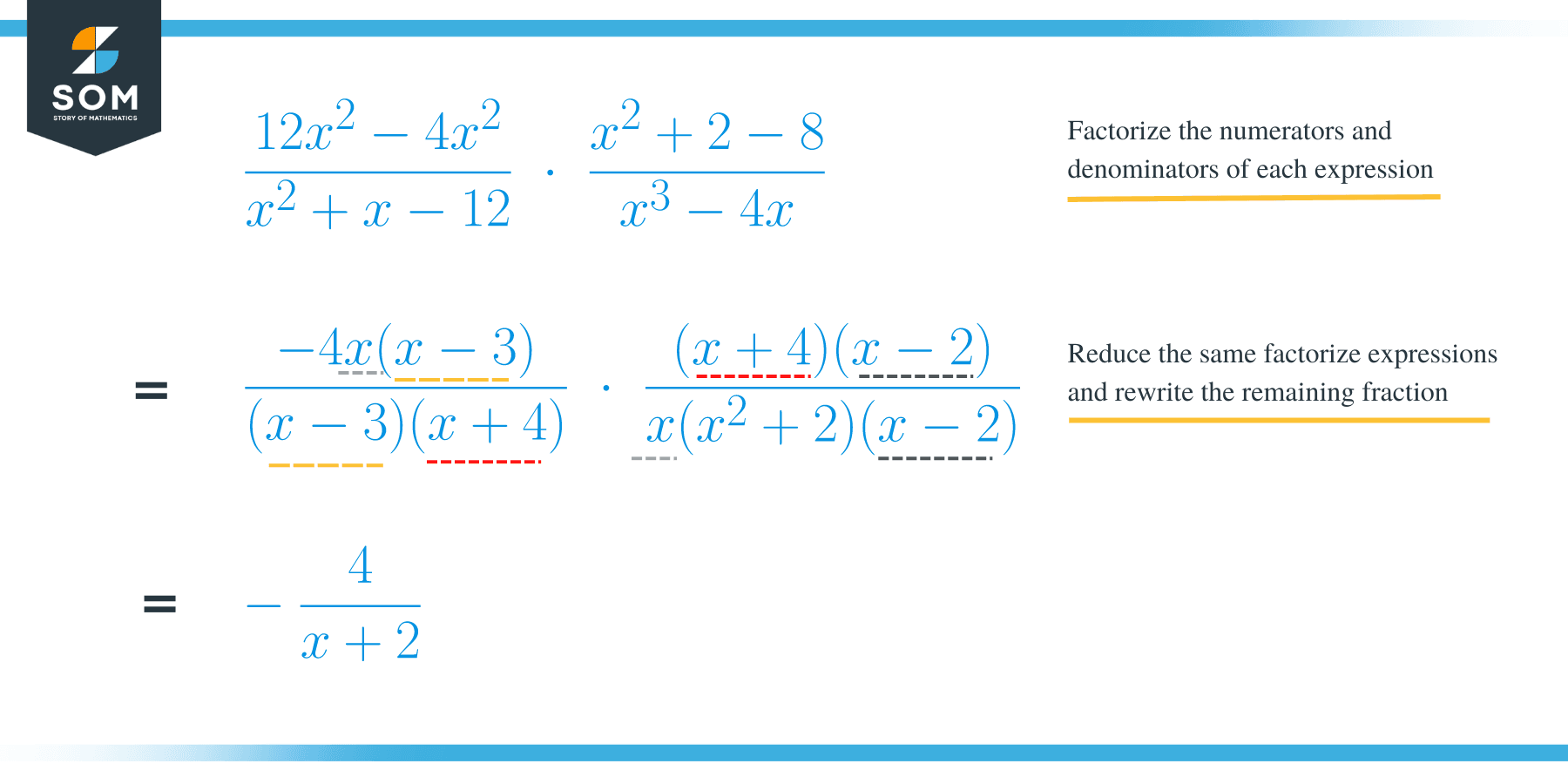

 

Example 3

Multiply (x ² – 3x – 4/x ² -x -2) * (x ² – 4/ x² + x – 20).

Solution

Factor the numerators and denominators of all expressions;

= (x – 4) (x + 1)/ (x + 1) (x – 2) * (x + 2) (x – 2)/ (x – 4) (x + 5)

Cancel out and rewrite the remaining factors;

= x + 2/ x + 5

 

Example 4

Multiply

(9 – x ²/x ² + 6x + 9) * (3x + 9/3x – 9)

Solution

Factor the numerators and denominators and cancel out common factors;

= – 1 (x + 3) (x – 3)/ (x + 3)² * 3(x + 3)/3(x – 30

= -1

 

Example 5

Simplify: (x²+5x+4) * (x+5)/(x²-1)

Solution

By factoring the numerator and denominator, we get;

=>(x+1) (x+4) (x+5)/(x+1) (x-1)

On canceling the common terms, we get;

=>(x+4) (x+5)/x-1

 

Example 6

Multiply ((x + 5) / (x – 4)) * (x / x + 1)

Solution

= ((x + 5) * x) / ((x – 4) * (x + 1))

= (x² + 5x) / (x² – 4x + x – 4)

= (x² + 5x) / (x² – 3x– 4)

When you multiply a whole number by an algebraic expression, you multiply the number by the expression’s numerator.

This is possible because any whole number always has a denominator of 1. And therefore, the multiplication rules between an expression and a whole does not change.

Consider the example 7 below:

Example 7

Multiply ((x + 5) / (x² – 4)) * x

Solution

= ((x + 5) / (x² – 4)) * x / 1

= (x + 5) * x / (x² – 4) × 1

= (x² + 5x) / (x² – 4)