- Home
- >
- Dividing Polynomials – Explanation & Examples
JUMP TO TOPIC
Dividing Polynomials – Explanation & Examples
 Division of polynomials might seem like the most challenging and intimidating of the operations to master. Still, so long as you can recall the basic rules about the long division of integers, it’s a surprisingly easy process.
Division of polynomials might seem like the most challenging and intimidating of the operations to master. Still, so long as you can recall the basic rules about the long division of integers, it’s a surprisingly easy process.
This article will show you how to carry out the division between two monomials, a monomial and polynomial, and lastly, between two polynomials.
Before getting into this topic of dividing polynomials, let’s briefly discuss a few important terms here.
Polynomial
A polynomial is an algebraic expression made up of two or more terms that are subtracted, added, or multiplied. A polynomial can contain coefficients, variables, exponents, constants, and operators such as addition and subtraction.
It is also important to note that, a polynomial can’t have fractional or negative exponents. Examples of polynomials are; 3y2 + 2x + 5, x3 + 2 x 2 − 9 x – 4, 10 x 3 + 5 x + y, 4x2 – 5x + 7) etc.
There are three types of polynomials, namely monomial, binomial and trinomial.
- Monomial
A monomial is an algebraic expression with only one term. Examples of monomials are; 5, 2x, 3a2, 4xy, etc.
- Binomial
A binomial is an expression containing two terms separated by either the addition sign (+) or subtraction sign (-). Examples of binomial expressions are 2x + 3, 3x – 1, 2x+5y, 6x−3y, etc.
- Trinomial
A trinomial is an expression that contains exactly three terms. Examples of trinomials are:
4x2 + 9x + 7, 12pq + 4x2 – 10, 3x + 5x2 – 6x3 etc.
How to Divide Polynomials?
The division is an arithmetic operation of splitting a quantity into equal amounts. The division process is sometimes referred to as repeated subtraction or reverse multiplication.
There are two methods in mathematics for dividing polynomials.
These are the long division and the synthetic method. As the name suggests, the long division method is the most cumbersome and intimidating process to master. On the other hand, the synthetic method is a “fun” way of dividing polynomials.
How to divide a monomial by another monomial?
When dividing a monomial by another monomial, we divide the coefficients and apply the quotient law x m ÷ x n = x m – n to the variables.
NOTE: Any number or variable raised to the power of zero is 1. For example, x0 = 1.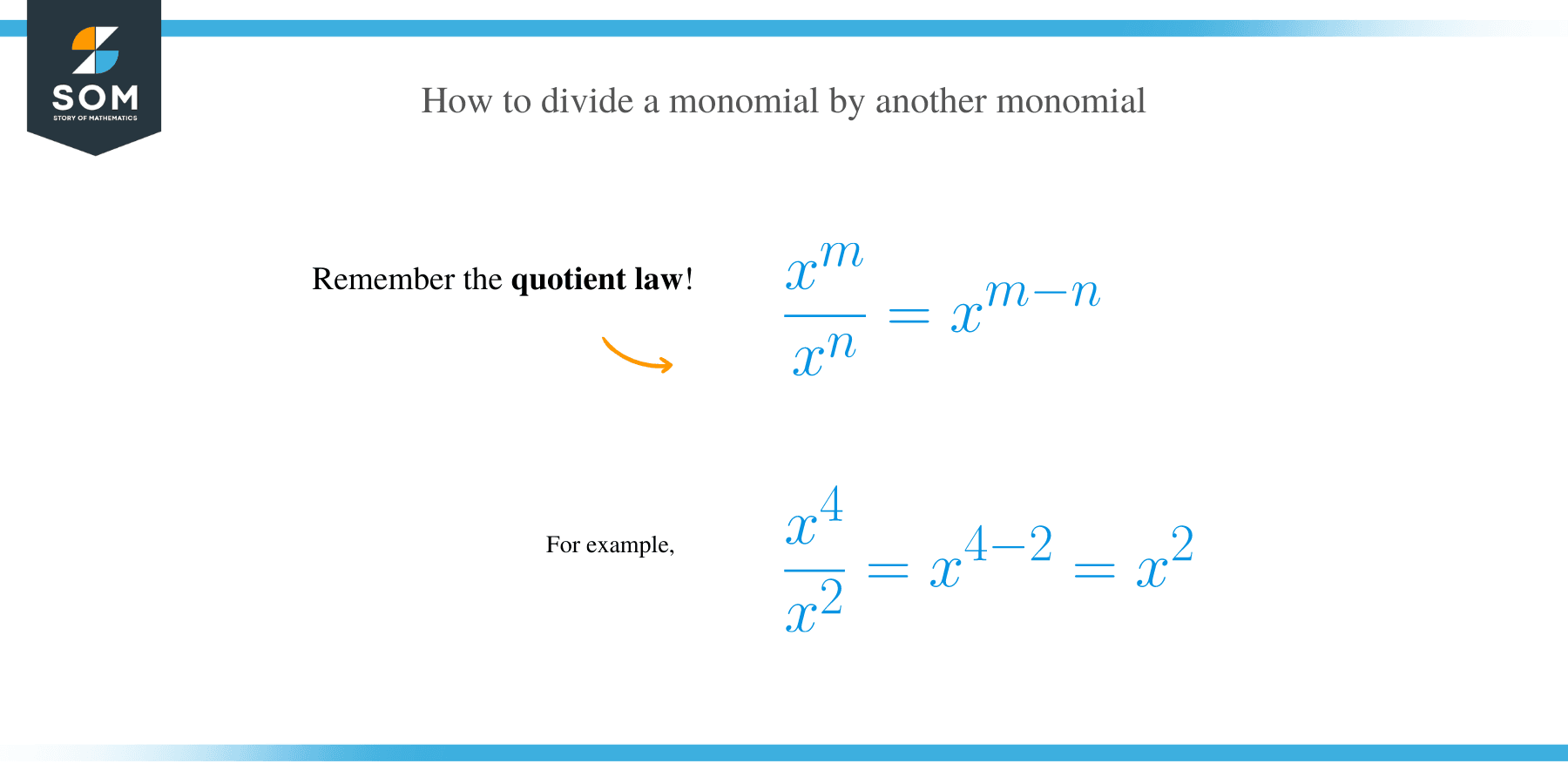
Let’s try a few examples here.
Example 1
Divide 40x2 by 10x
Solution
Divide the coefficients first
40/10 = 4
Now divide the variables using the quotient rule
x2 /x = x2 -1
= x
Multiply the quotient of the coefficients by the quotients of the variables;
⟹ 4* x = 4x
Alternatively;
40x2/10x = (2 * 2 * 5 * 2* x * x)/ (2 * 5 * x)
Since x, 2, and 5 are common factors of both the denominator and numerator, we cancel them out to get;
⟹ 40x2/10x = 4x
Example 2
Divide -15x3yz3 by -5xyz2
Solution
Divide the coefficients normally and use the quotient law x m ÷ x n = x m – n to divide the variables.
-15x3yz3 / -5xyz2 ⟹ (-15/-5) x3 – 1y1 – 1z3 – 2
= 3 x2y0z1
= 3x2z.
Example 3
Divide 35x3yz2 by -7xyz
Solution
Using the Quotient law
35x3yz2 / -7xyz ⟹ (35/-7) x3 – 1y1 – 1z2 – 1
= -5 x2y0z1
= -5x2z.
Example 4
Divide 8x2y3 by -2xy
Solution
8x2y3/-2xy ⟹ (8/-2) x2 – 1y3 – 1
= -4xy2.
How to divide polynomials by monomials?
To divide a polynomial by a monomial, separately divide each term of the polynomial by the monomial and add each operation’s quotient to get the answer.
Let’s try a few examples here.
Example 5
Divide 24x3 – 12xy + 9x by 3x.
Solution
(24x3–12xy + 9x)/3x ⟹ (24x3/3x) – (12xy/3x) + (9x/3x)
= 8x2 – 4y + 3
Example 6
Divide 20x3y + 12x2y2 – 10xy by 2xy
Solution
(20x3y + 12x2y2 – 10xy) /(2xy) ⟹ 20x3y /2xy + 12x2y2/2xy – 10xy/2xy
= 10x2 + 6xy – 5.
Example 7
Divide x6 + 7x5 – 5x4 by x2
Solution
= (x6 + 7x5 – 5x4)/ (x2) ⟹ x6 /x2 + 7x5/x2 – 5x4/x2
Use the Quotient law to divide the variables
= x4 + 7x3 − 5x2
Example 8
Divide 6x5 + 18x4 – 3x2 by 3x2
Solution
= (6x5 + 18x4 – 3x2)/3x2 ⟹ 6x5/3x2 + 18x4/3x2 – 3x2/3x2
=2x3 + 6x2 – 1.
Example 9
Divide 4m4n4 – 8m3n4 + 6mn3 by -2mn
Solution
= (4m4n4 – 8m3n4 + 6mn3)/(-2mn) ⟹ 4m4n4/- 2mn – 8m3n4/-2mn + 6mn3/-2mn
= 2m3n3 + 4m2n3 – 3n2
Example 9
Solve (a3 – a2b – a2b2) ÷ a2
Solution
= (a3 – a2b – a2b2) ÷ a2 ⟹ a3/ a2– a2b/ a2 – a2b2/ a2
= a – b – b2
How to do polynomial long division?
The long division is the most suitable and reliable method of dividing polynomials, even though the procedure is a bit tiresome, the technique is practical for all problems.
The process of dividing polynomials is just similar to dividing integers or numbers using the long division method.
To divide two polynomials, here are the procedures:
- Arrange both the divisor and dividend in descending order of their degrees.
- Divide the 1st term of the dividend by the 1st term of the divisor to obtain the 1st term of the quotient.
- Find the product of all the terms of the divisor and the 1st term quotient and subtract the dividend’s answer.
- If there is a remainder in the above, proceed as repeat procedure 3 until till you get zero as the remainder or you obtain an expression having a smaller degree than that of the divisor.
Example 10
Divide the following polynomials using long division method:
3x3 – 8x + 5 by x – 1
Solution

Example 11
Divide 12 – 14a² – 13a by 3 + 2a.
Solution

Example 12
Divide the polynomials below:
10x⁴ + 17x³ – 62x² + 30x – 3 by (2x² + 7x – 1).
Solution

