Solving Inequalities – Explanation & Examples

What is Inequality in Math?

The word inequality means a mathematical expression in which the sides are not equal to each other. Basically, an inequality compares any two values and shows that one value is less than, greater than, or equal to the value on the other side of the equation.

Basically, there are five inequality symbols used to represent equations of inequality.

Inequality Symbols

These inequality symbols are: less than (<), greater than (>), less than or equal (≤), greater than or equal (≥) and the not equal symbol (≠).

Inequalities are used to compare numbers and determine the range or ranges of values that satisfy the conditions of a given variable.

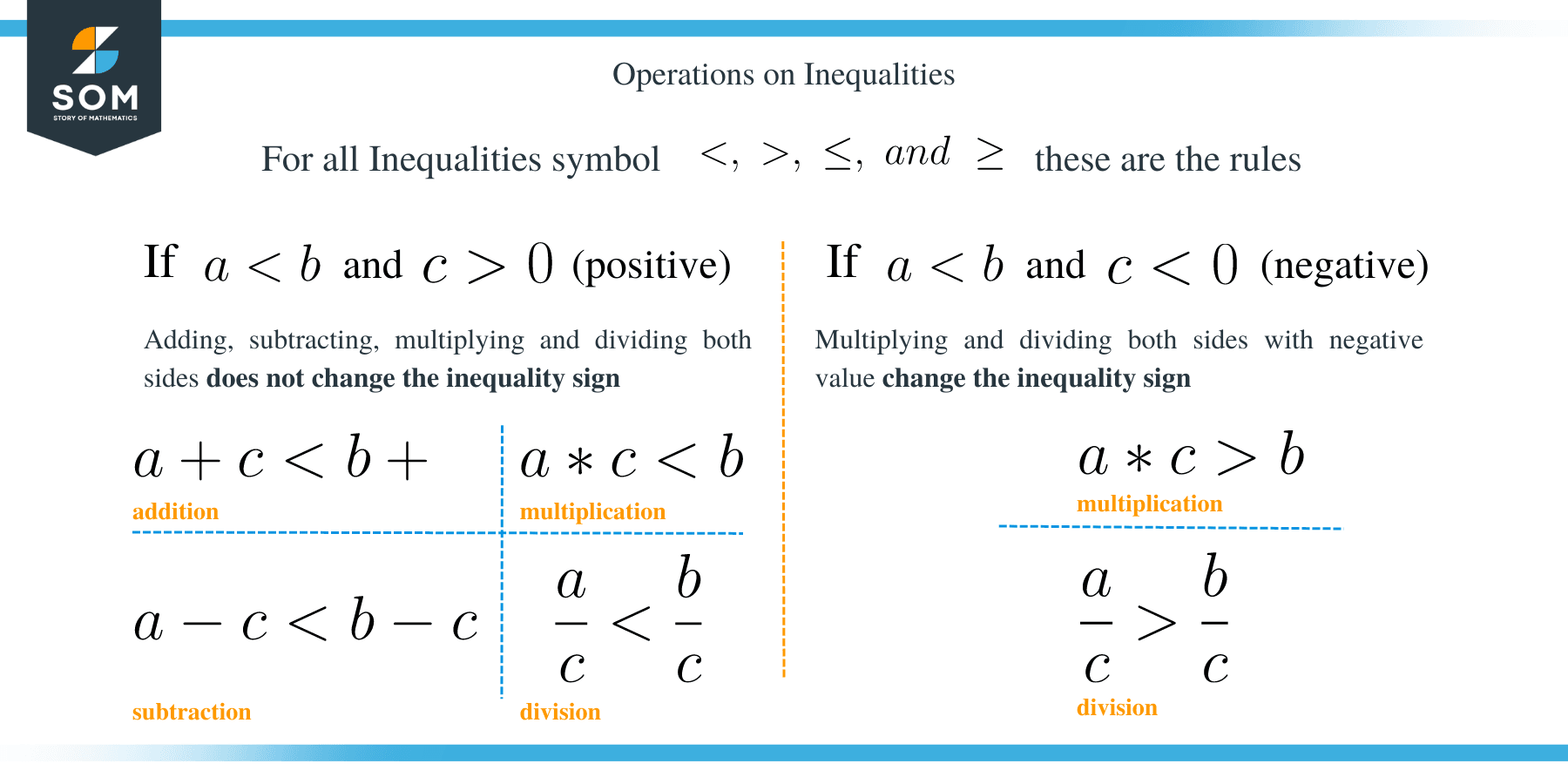
Operations on Inequalities

Operations on linear inequalities involve addition, subtraction, multiplication, and division. The general rules for these operations are shown below.

Although we have used < symbol for illustration, you should note that the same rules apply to >, ≤, and ≥.

• The inequality symbol does not change when the same number is added on both sides of the inequality. For example, if a< b, then a + c < b +
• Subtracting both sides of the inequality by the same number does not change the inequality sign. For example, if a< b, then a – c < b – c.
• Multiplying both sides of an inequality by a positive number does not change the inequality sign. For example, if a< b and if c is a positive number, then a * c < b *
• Dividing both sides of an inequality by a positive number does not change the inequality sign. If a< b and if c is a positive number, then a/c < b/c
• Multiplying both sides of an inequality equation by a negative number changes the direction of the inequality symbol. For example, given that a < b and c is a negative number, then a * c > b *
• Similarly, dividing both sides of an inequality equation by a negative number changes the inequality symbol. If a < b and if c is a negative number, then a /c > b/c

How to Solve Inequalities?

Like linear equations, inequalities can be solved by applying similar rules and steps with a few exceptions. The only difference when solving linear equations is an operation that involves multiplication or division by a negative number. Multiplying or dividing an inequality by a negative number changes the inequality symbol.

Linear inequalities can be solved using the following operations:

• Addition
• Subtraction
• Multiplication
• Division
• Distribution of property

Solving linear inequalities with addition

Let’s see a few examples below to understand this concept.

Example 1

Solve 3x − 5 ≤ 3 − x.

Solution

We start by adding both sides of the inequality by 5

3x – 5 + 5 ≤ 3 + 5 − x

3x ≤ 8 – x

Then add both sides by x.

3x + x ≤ 8 – x + x

4x ≤ 8

Finally, divide both sides of the inequality by 4 to get;

x ≤ 2

 

Example 2

Calculate the range of values of y, which satisfies the inequality: y − 4 < 2y + 5.

Solution

Add both sides of the inequality by 4.

y – 4 + 4 < 2y + 5 + 4

y < 2y + 9

Subtract both sides by 2y.

y – 2y < 2y – 2y + 9

Y < 9 Multiply both sides of the inequality by −1 and change the inequality symbol’s direction. y > − 9

 

Solving linear inequalities with subtraction

Let’s see a few examples below to understand this concept.

 

Example 3

Solve x + 8 > 5.

Solution

Isolate the variable x by subtracting 8 from both sides of the inequality.

x + 8 – 8 > 5 – 8 => x > −3

Therefore, x > −3.

 

Example 4

Solve 5x + 10 > 3x + 24.

Solution

Subtract 10 from both sides of the inequality.

5x + 10 – 10 > 3x + 24 – 10

5x > 3x + 14.

Now we subtract both sides of the inequality by 3x.

5x – 3x > 3x – 3x + 14

2x > 14

x > 7

 

Solving linear inequalities with multiplication

Let’s see a few examples below to understand this concept.

Example 5

Solve x/4 > 5

Solution:

Multiply both sides of an inequality by the denominator of the fraction

4(x/4) > 5 x 4

x > 20

 

Example 6

Solve -x/4 ≥ 10

Solution:

Multiply both sides of an inequality by 4.

4(-x/4) ≥ 10 x 4

-x ≥ 40

Multiply both sides of the inequality by -1 and reverse the direction of the inequality symbol.

x ≤ – 40

 

Solving linear inequalities with division

Let’s see a few examples below to understand this concept.

 

Example 7

Solve the inequality: 8x − 2 > 0.

Solution

First of all, add both sides of the inequality by 2

8x – 2 + 2 > 0 + 2

8x > 2

Now, solve by dividing both sides of the inequality by 8 to get;

x > 2/8

x > 1/4

 

Example 8

Solve the following inequality:

−5x > 100

Solution

Divide both sides of the inequality by -5 and change the direction of the inequality symbol

= −5x/-5 < 100/-5

= x < − 20

 

Solving linear inequalities using the distributive property

Let’s see a few examples below to understand this concept.

Example 9

Solve: 2 (x – 4) ≥ 3x – 5

Solution

2 (x – 4) ≥ 3x – 5

Apply the distributive property to remove the parentheses.

⟹ 2x – 8 ≥ 3x – 5

Add both sides by 8.

⟹ 2x – 8 + 8 ≥ 3x – 5 + 8

⟹ 2x ≥ 3x + 3

Subtract both sides by 3.

⟹ 2x – 3x ≥ 3x + 3 – 3x

⟹ -x ≥ 3

⟹ x ≤ – 3

 

Example 10

A student scored 60 marks in the first test and 45 marks in the second test of the terminal examination. How many minimum marks should the student score in the third test get a mean of least 62 marks?

Solution

Let the marks scored in the third test be x marks.

(60 + 45 + x)/3 ≥ 62
105 + x ≥ 196
x ≥ 93
Therefore, the student must score 93 marks to maintain a mean of at least 62 marks.

 

Example 11

Justin requires at least $500 to hold his birthday party. If already he has saved $ 150 and 7 months are left to this date. What is the minimum amount he must save monthly?

Solution

Let the minimum amount saved monthly = x

150 + 7x ≥ 500

Solve for x

150 – 150 + 7x ≥ 500 – 150

x ≥ 50

Therefore, Justin should save $50 or more

 

Example 12

Find two consecutive odd numbers which are greater than 10 and have the sum of less than 40.

Solution

Let the smaller odd number = x

Therefore, the next number will be x + 2

x > 10 ………. greater than 10

x + (x + 2) < 40 ……sum is less 40

Solve the equations.

2x + 2 < 40

x + 1< 20

x < 19

Combine the two expressions.

10 < x < 19

Therefore, the consecutive odd numbers are 11 and 13, 13 and 15, 15 and 17, 17 and 19.

 

Inequalities and the Number Line

The best tool to represent and visualize numbers is the number line. A number line is defined as a straight horizontal line with numbers placed along at equal segments or intervals. A number line has a neutral point at the middle, known as the origin. On the right side of the origin on the number line are positive numbers, while the left side of the origin is negative numbers.

Linear equations can also be solved by a graphical method using a number line. For example, to plot x > 1, on a number line, you circle the number 1 on the number line and draw a line going from the circle in the direction of the numbers that satisfies the inequality statement.

 

Example 13

If the inequality symbol is greater than or equal to or less than or equal to sign (≥ or ≤), draw the circle over the numerical number and fill or shade the circle. Finally, draw a line going from the shaded circle in the numbers’ direction that satisfies the inequality equation.

 

Example 14

x ≥ 1

The same procedure is used to solve equations involving intervals.

 

 Example 15

–2 < x < 2

Example 16

–1 ≤ x ≤ 2

 

Example 17

–1 < x ≤ 2