Addition Property of Equality – Definition and Examples

The addition property of equality states that if equal quantities each have an equal amount added on to them, then the sums are still equal.

It essentially says that if there are two containers with equal amounts of water, then the containers will still have equal amounts of water when one gallon of water is added to each.  

Both arithmetic and algebra use the addition property of equality.

Before moving on with this section, make sure to review properties of equality and properties of addition, particularly the commutative property first.

This section covers:

• What Is the Addition Property of Equality?
• Addition Property of Equality Definition
• Commutativity and the Addition Property of Equality
• Example of Addition Property of Equality
  

What Is the Addition Property of Equality?

The addition property of equality is a truth about equal quantities. That is, it is true any time there are two or more amounts related with an equal sign.

Arithmetic utilizes the addition property of equality to develop number sense and compare numeric quantities. Algebra also uses it as a strategy to isolate a variable.

Addition Property of Equality Definition

Euclid defines the addition property of equality in Book 1 of his Elements when he says, “when equals be added to equals, the sums are equal.” He referenced this fact so often that he called it “common notion 1,” so it would be easier to cite.

Another way to say this is that when the same amount is added to two quantities that are already equal, it doesn’t change the equality.

Arithmetically, this is:

If $a=b$, then $a+c=b+c$.

The inverse is also true. That is, if different amounts are added to equal quantities, the sums are no longer equal.

Arithmetically, this is:

If $a=b$ and $c\neq d$ then $a+c$ is not equal to $b+d$.

This may seem like an obvious fact that it is not worth stating. On the contrary, however, it has far-reaching implications.

Euclid used this truth in many proofs in his Elements, which helped shape the mathematical knowledge of Western Civilization.

The addition property of equality is also used in algebra when any quantity is subtracted from a variable. This is because adding back the subtracted quantity helps isolate the variable and solve for its value.

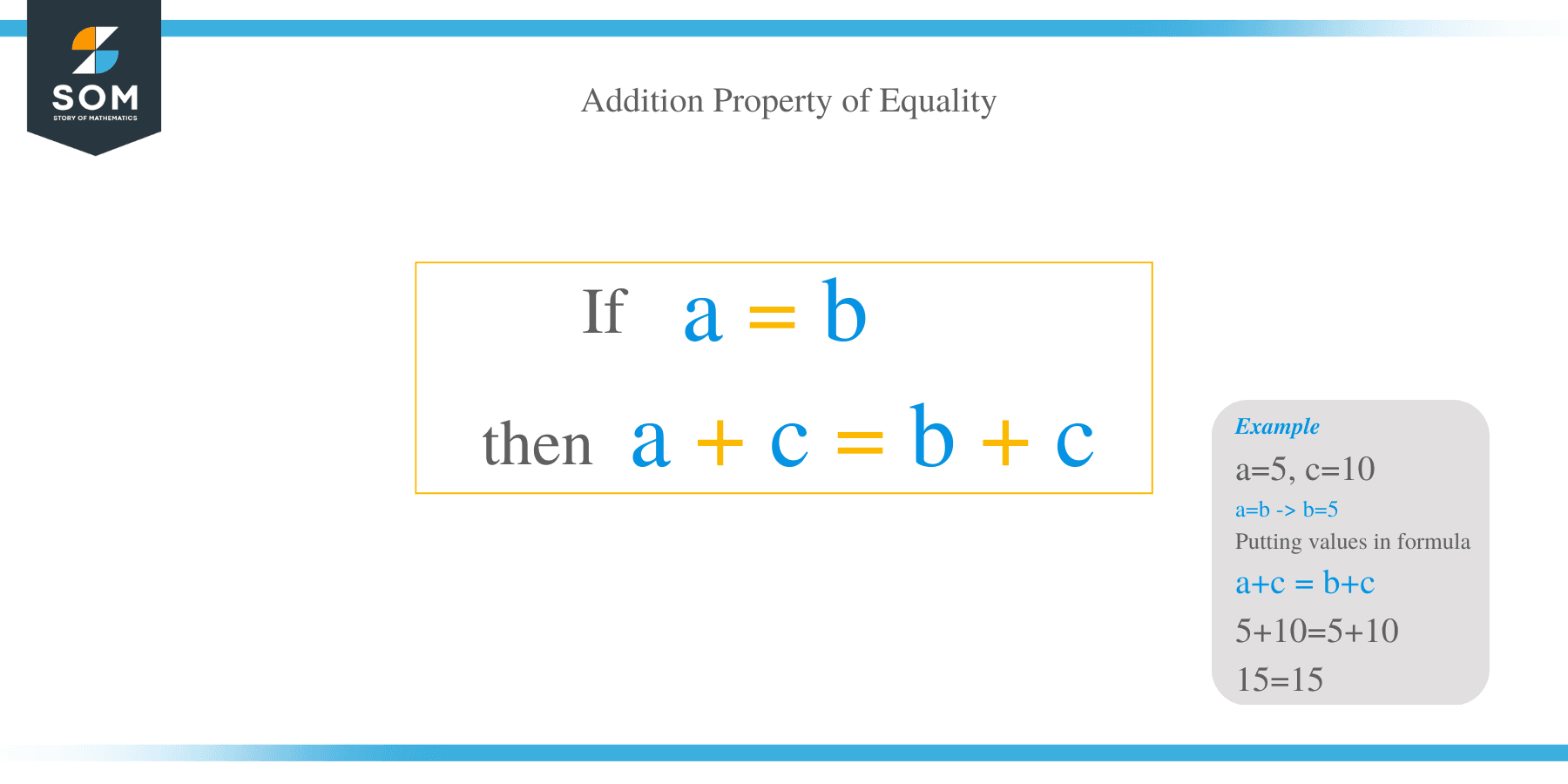
Commutativity and the Addition Property of Equality

Recall that addition is commutative. That means that changing the order of the operations does not change the resulting sum.

Arithmetically, $a+b=b+a$.

It is possible to combine commutativity with the addition property of equality. Suppose $a, b, c$ are real numbers and $a=b$. Then the addition property of equality states:

$a+c=b+c$

Commutativity states that:

$a+c=c+b$, $c+a=b+c$, and $c+a=c+b$

Examples of Addition Property of Equality

This section covers common examples of problems involving the addition property of equality and their step-by-step solutions.

Example 1

Let $a, b, c$, and $d$ be real numbers. If $a$ is equal to $b$ and $c$ is equal to $d$, which of the following are equivalent and why?

• $a+c$ and $b+c$
• $a+c$ and $b+d$
• $a+b$ and $c+d$

Solution

The first two groups are equivalent while the last one is not.

$a+c=b+c$ because $a=b$. Adding $c$ to both means that the same quantity is added to both sides. This is the very definition of the addition property of equality.

$a+c=b+d$ because $a=b$ and $c=d$. We know that $a+c=b+c=b+d$. Therefore, $a+c=b+d$ since they are both equal to $b+c$.

The last one is not necessarily equal since a is not equal to $c$ or $d$ and $b$ is not equal to $c$ or $d$. Since $a=b$ and $c=d$, $a+b$ is equal to $2a$ or $2b$. Likewise, $c+d$ is equal to $2c$ or $2d$. $2a \neq 2c$ and $2a \neq 2d$. Similarly, $2b \neq 2c$ and $2b \neq 2d$.

Example 2

Jack and Denzel are the same height. Each boy then grows two inches taller. How do their heights compare after they have grown taller?

Solution

Jack and Denzel are still the same height after they grew taller.

Let $j$ be Jack’s height in inches and $d$ be Denzel’s height in inches. Based on the given information $j=d$.

After Jack grows two inches taller, his height is $j+2$.

After Denzel grows two inches taller, his height is $d+2$.

Since each grew the same amount, 2 inches, the addition property of equality says that they will still be the same height.

That is, $j+2=d+2$.

Example 3

The amount of product Kayla brings to a craft show is represented by the expression $k+5+3$.

The amount of product Frankie brings to a craft show is represented by the expression $f+3+5$.

If $k=f$, who brought more product to the craft show?

Solution

Each person brings the same amount of product to the craft show.

Kayla brings $k+5+3$ products. Since $5+3=8$, this expression simplifies to $k+8$.

Frankie brings $f+3+5$ products. Since $3+5=8$, this expression simplifies to $f+8$.

Since $k=f$, the additive property of equality states that $k+8=f+8$. Therefore, $k+5+3=f+3+5$.

Therefore, both people bring the same amount of product.

Example 4

One line has length $m$ centimeters and another has length $n$ centimeters. The two lines are the same length.

The line with length $m$ is extended by 4 centimeters, and the length of $n$ is extended four times.

Jeremy considers this situation and says that the two new lines will also have the same length because of the addition property of equality. What is his mistake?

Solution

Although the two original lines, $m$ and $n$, have the same length, the new lines will not have the same length. This is because the two lines do not have the same amount of length added onto them.

The length of the first line increases by 4 centimeters. That is, the line’s new length is $m+4$ centimeters.

On the other hand, the length of the second line increases by four times. This means that the length of the new line is $4n$ centimeters.

Note that $4n=n+3n$.

Therefore, the new lines are $m+4$ centimeters and $n+3n$ centimeters. Even though $m$ and $n$ are equal, the new lines are not equal unless $4=3n$. Since it is not stated that these two quantities are the same, the resulting lines are not known to be equal.

Example 5

Recall that the addition property of equality is true for all real numbers. Use this fact to prove the subtraction property of equality.

That is, prove that:

If $a=b$, then $a-c=b-c$ for any real number, $c$.

Solution

Let $n, a,$ and $b$ be real numbers, and let $a=b$. The addition property of equality states that:

$a+n=b+n$

Since $n$ is a real number, $-n$ is also a real number. Therefore:

$a+(-n)=b+(-n)$

Adding a negative is the same as subtracting, so this equation simplifies to:

$a-n=b-n$

Thus, the subtraction property of equality follows from the addition property of equality. That is, for any real numbers $a, b,$ and $n$ where $a=b$, $a-n=b-n$ as required.

QED.