• Home
  • >
  • Angle of Elevation — Detailed Explanation and Examples

Angle of Elevation – Explanation & Examples

When you look up at an item above you, you can measure the angle of elevation between the item and the ground. Let’s suppose you are taking a walking tour in Tuscany — a region in central Italy. Suddenly, you can’t walk any further and need to stop for a small rest. While you are looking straight ahead, someone asks you to raise your eyes to see the magic. You elevate your eyes to witness the iconic leaning Tower of Pisa within walking distance. What can you determine when you look at the top of the Pisa Tower?

The angle of elevation is basically the measure of an angle between the horizontal line and line of sight of a person’s eyes to some item above. The angle of elevation depends upon the movement of the observer’s eyes. 

With this lesson, we aim to clarify any confusion you might have about the concept of the angle of elevation.

What Is an Angle of Elevation?

When an observer is looking up at an object, the angle made by the line of sight with the horizontal line is called the angle of elevation.

Let us consider a vertical wall with its base fixed to the ground, as shown in Figure 11-1. Let’s say a man is standing some distance away from the wall and looking straight at it. The line drawn from the man’s eye to the far point where the man is staring is known as the line of sight. Since this line is parallel to the ground, we call it the horizontal light of sight — or simply a horizontal line.

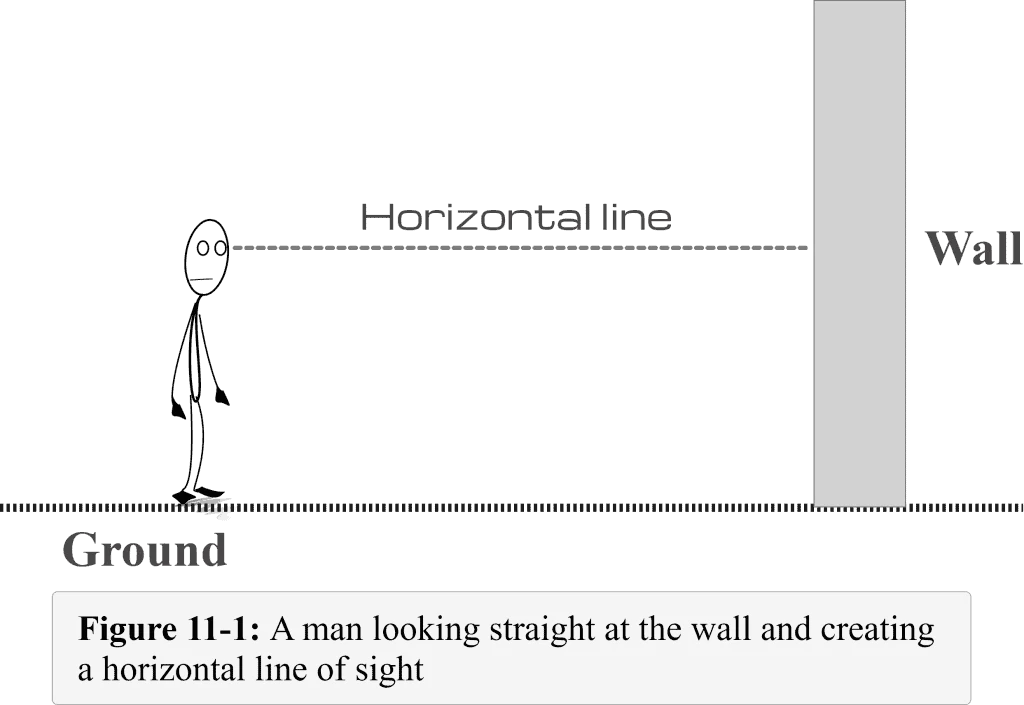
Figure 11 1 A man looking straight at the wall and creating a horizontal line of sight

Now, if the man is looking at the top of the wall, what should the line of sight be?

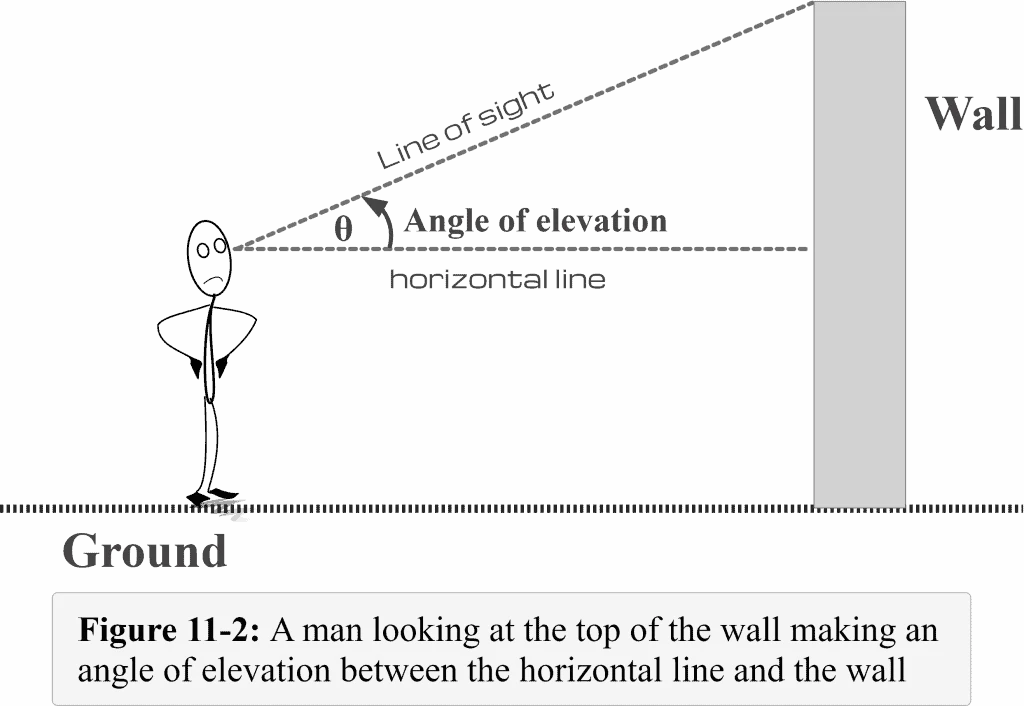
Figure 11 2 A man looking at the top of the wall and making an angle of elevation

The above Figure 11-2 shows that the line drawn from the eye to the top of the wall would be the line of sight. We can easily observe that this line of sight makes some angle with the horizontal line. This angle is called the angle of elevation. You need to ponder that the line of sight is above the horizontal line.

Looking at Figure 11-2, the angle $\theta$ represents the angle of elevation to the top of the wall as seen through the eyes of an observer on the ground.

How To Find the Angle of Elevation

In figure 11.3, a man is standing $3$ m from the building and looking at the top of it. Assume the man is $1.5$ m tall up to his eyes. The height of the building from the horizontal line (eye level of the man) to the top is $5.2$ m. Let us determine the angle of elevation formed by the line of sight with the horizontal line.

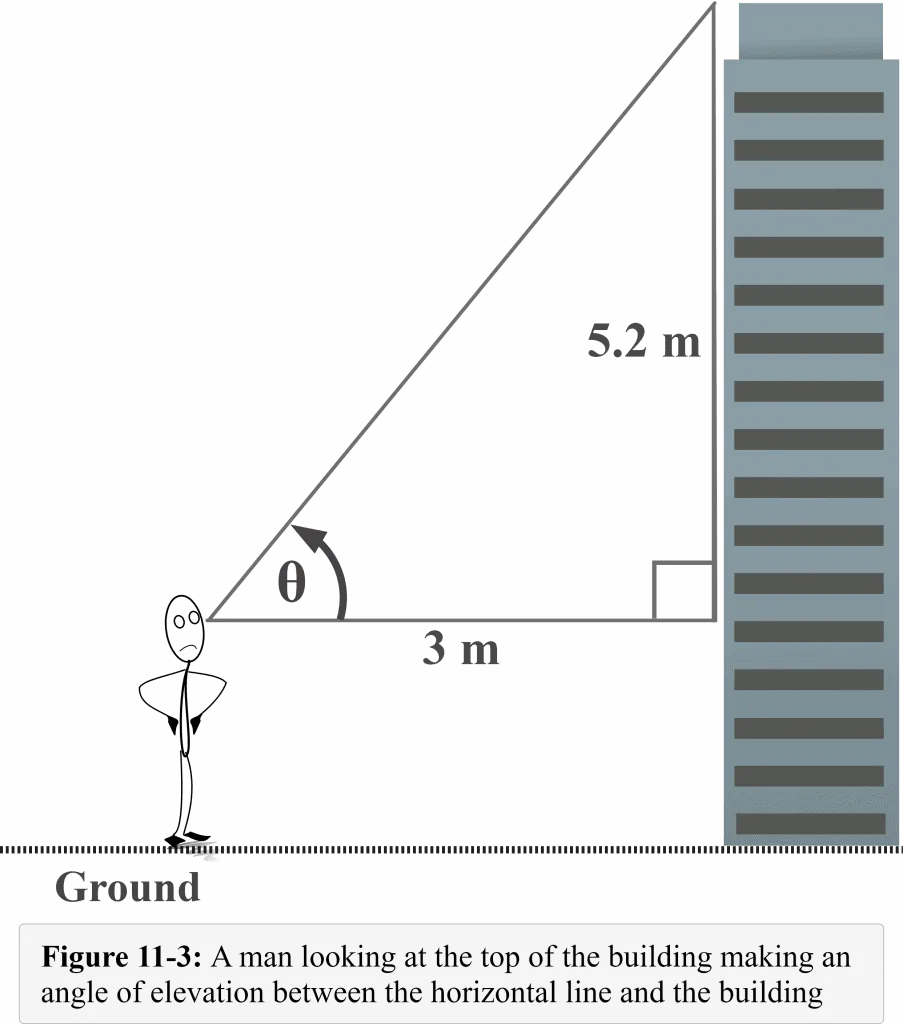
Figure 11 3 A man looking at the top of the building and making an angle of elevation

Let $\theta%%EDITORCONTENT%%nbsp;$ be the required angle of elevation.

Looking at the diagram, it is clear that a right triangle is formed. The terms opposite, adjacent, and hypotenuse are called the lengths of sides.

In our wall example, the side of length $3$ m is the adjacent side that lies right next to the reference angle $\theta$ (angle of elevation), and the side of length $5.2$ m is the opposite side that lies exactly opposite the angle $\theta$. Thus,

Adjacent = $3$ m

Opposite = $5.2$ m

We know that the tangent function is the ratio of the opposite side to the adjacent side.

Using the formula of the tangent function:

${\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

substitute opposite = $5.2$, and adjacent = $3$ in the formula

${\displaystyle \tan \theta ={\frac {5.2}{3}}}$

$\tan \theta = 1.73333333$

solving the equation

$\theta =\tan^{-1}(1.73333333)$

$\theta ≈ 60^{\circ }$ (You can check the calculator to verify)

Therefore, the measure of the required angle of elevation θ is approximately $60^{\circ }$.

Example 1

Mr. Pirlo, who is $6$ feet tall, observes that the angle of elevation to the top of a palm tree at a distance of $40$ feet is $32^{\circ }$. Determine the height of the tree.

Solution:

Step 1 of 3

Create a clear diagram displaying the known measurements

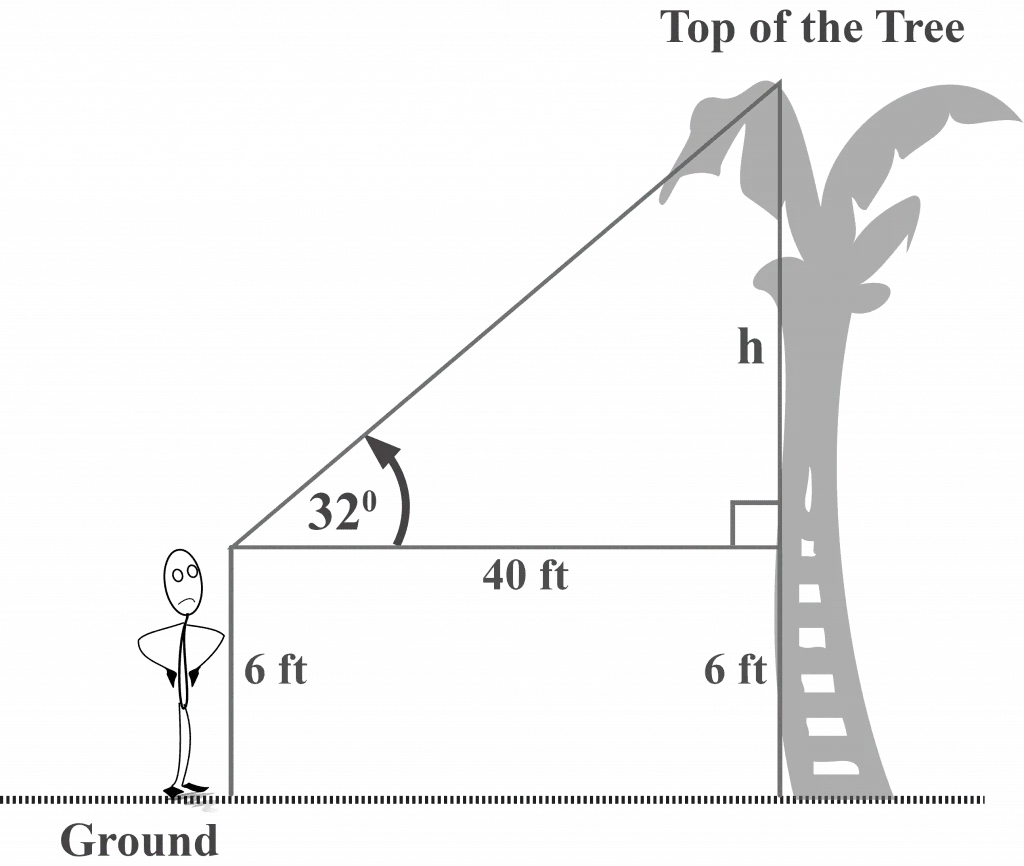
A man observing the angle of elevation as he looks at the top of the tree

Step 2 of 3

Figure out the relationship between the quantities in the diagram to establish equations containing trigonometric ratios.

Looking at the diagram, it is clear that:

Angle of elevation $\theta = 32^{\circ }$

The height of Mr. Pirlo = $6$ feet

Adjacent = $40$ feet

Opposite = $h$ feet

Let the required height of the tree be = $h +$ height of Mr. Pirlo

= $h + 6$

Using the formula of the tangent function:

${\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

substitute opposite = $h$, $\theta = 32^{\circ }$ and adjacent = $40$ in the formula

${\displaystyle \tan 32^{\circ } = {\frac {{h}}{40}}}$

Step 3 of 3

Use a calculator or table to determine the answer.

${\displaystyle \tan 32^{\circ } = {\frac {{h}}{40}}}$

$0.62486935 = {\frac {{h}}{40}}$

$h = 24.9947741$

$h ≈ 25.0$ feet (Rounded to the tenth place)

Required height = $h + 6$

= $25 + 6$

= $31$ feet

Thus, the required height of the tree is $31$ feet.

Example 2

A vertical pool of length $8$ m casts a $6$ m shadow. Find the measure of the angle of elevation of the sun at the moment.

Solution:

First, create a clearly labeled diagram showing the known measurements.

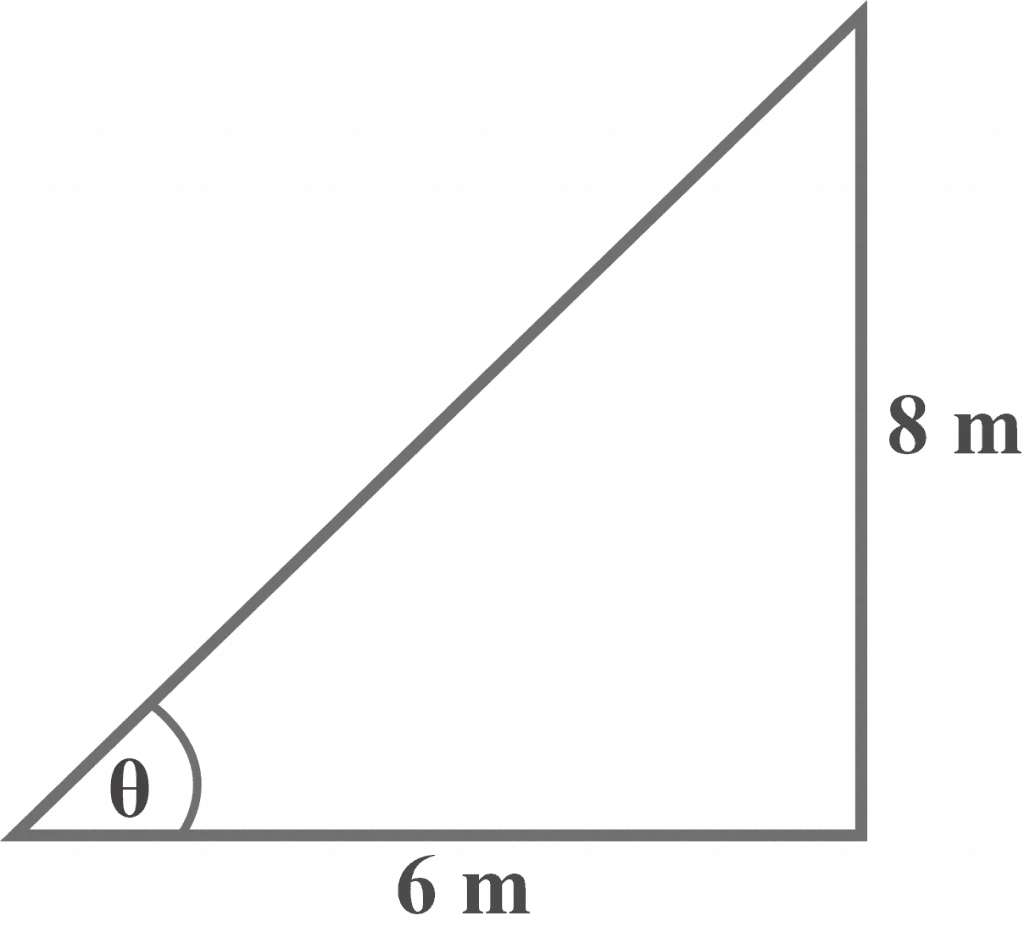
Measuring of the angle of elevation of the sun at the moment.

Let $\theta$ be the required angle of elevation.

Looking at the diagram, it is clear that:

Adjacent $= 6$ m

Opposite $= 8$ m

Using the formula of the tangent function:

${\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

substitute opposite = $8$, and adjacent = $6$ in the formula

${\displaystyle \tan \theta = {\frac {{8}}{6}}}$

$\tan \theta = 1.33333333$

solving the equation

$\theta =\tan^{-1}(1.33333333)$

$\theta ≈ 53.13^{\circ }$

Therefore, the measure of the angle of elevation of the sun at the moment is $53.13^{\circ }$.

Example 3

Let $A$ and $B$ be the two points in line with a flag. If the distance between $A$ and $B$ is $100$ feet and the angle of elevation to the top of the flag at $A$ and $B$ measures $12^{\circ }$ and $15^{\circ }$, respectively, what is the height of the flag?

Solution:

First, create a simple labeled diagram showing the known measurements and depicting the scenario as shown below.

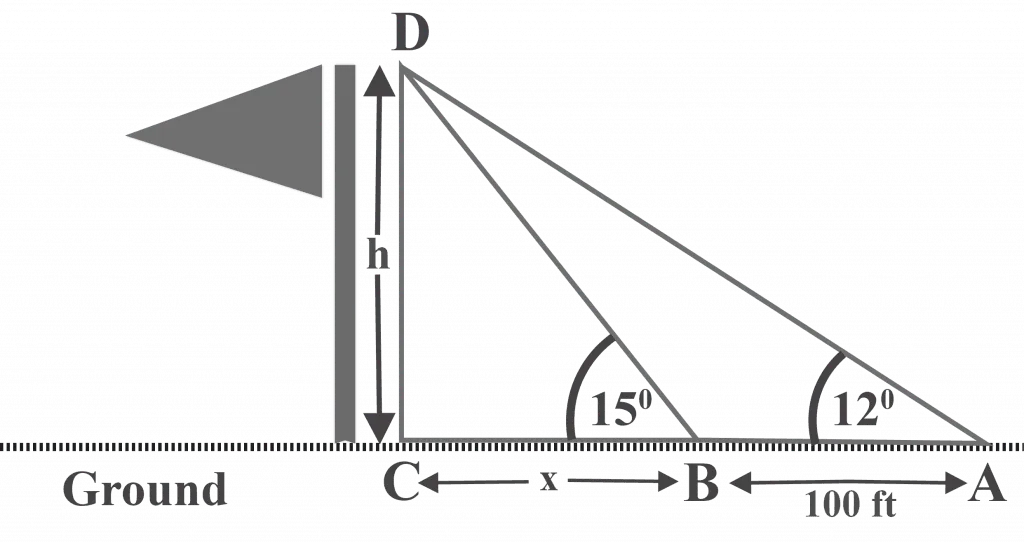
Measuring the height of the flag when angle of elevations are given

Let the height of the flag be = $h$

Looking at the diagram, first consider △DBC

$\theta = 15^{\circ }$

Opposite = $h$

Adjacent = $x$

Using the formula of the tangent function:

${\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

substitute opposite = $h$, $\theta = 15^{\circ }$ and adjacent = $x$ in the formula

${\displaystyle \tan 15^{\circ } = {\frac {{h}}{x}}}$

$h = x\tan 15^{\circ }%%EDITORCONTENT%%nbsp;     — $[1]$

Now we consider △DAC

$\theta = 12^{\circ }$

Opposite = $h$

Adjacent = $x+100$

Using the formula of the tangent function:

${\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

substitute opposite = $h$, $\theta = 12^{\circ }$ and adjacent = $x+100$ in the formula

${\displaystyle \tan 12^{\circ } = {\frac {{h}}{x+100}}}$

$h = (x+100)\tan 12^{\circ }%%EDITORCONTENT%%nbsp;     — $[2]$

tan θ = opposite / adjacent

Using equations $1$ and $2$

$x \tan 15^{\circ } = (x + 100) \tan 12^{\circ }$

$x \tan 15^{\circ } = x \tan 12^{\circ } + 100\tan 12^{\circ }$

$x \tan 15^{\circ } – x \tan 12^{\circ } =   100\tan 12^{\circ }$

$x (\tan 15^{\circ } –  \tan 12^{\circ }) =  100\tan 12^{\circ }$

$x(0.26794919 – 0.21255656) = 100 \tan 12^{\circ }$

$x(0.05539263) = 100(0.21255656)$

$(0.05539263)x = 21.5556562$

$x = 383.727152$

$x ≈ 383.7$ (Rounded to the tenth place)

substitute $x = 383.7$ in equation $1$

$h = x \tan 15^{\circ }$

$h = 383.7 (0.26794919)$

$h = 102.812104$

$h ≈ 102.8$ feet

Therefore, the height of the flag is $102.8$ feet.

Practice Questions

1. The string of a flying kite is $100$ meters, and its angle of elevation is $45^{\circ }$. If the string of the kite is fully stretched, what is the height of the kite above the ground?

2. Mr. Johnson, $5$ feet tall, observes that the angle of elevation of the top of the building at a distance of $50$ feet is $45^{\circ }$. What is the height of the building?

3. A vertical flag of length $10$ m casts a $5$ m shadow. What is the measure of the angle of elevation of the sun at the moment?

4. The two friends, Mr. Tim and Mr. Cook are on the opposite sides of the building. The length of a building is $100$ meters. What will be the distance between them if the angle of elevation of the top of the building measures $18^{\circ }$ and $22^{\circ }$, respectively?

5. Mr. A is working in a restaurant building. Mr. B, at a distance of $10$ meters from the building, finds the angle of elevation of Mr. A to be $30^{\circ }$. Mr. A climbs up $6$ meters, and the observer moves $2$ meters farther from the building. What is the new angle of elevation of Mr. A?


 

Previous Lesson | Main Page | Next Lesson