Area of an Ellipse – Explanation & Examples
In geometry, an is a two-dimensional flat elongated circle that is symmetrical along its shortest and longest diameters. An ellipse resembles an oval shape. In an ellipse, the longest diameter is known as the major axis, whereas the shortest diameter is known as the minor axis.
The distance of two points in the interior of an ellipse from a point on the ellipse is same as the distance of any other point on the ellipse from the same point. These points inside the ellipse are termed as foci. In this article, you will what an ellipse is, and how to find its area by using the area of an ellipse formula. But first see its few applications first.
Ellipses have multiple applications in the field of engineering, medicine, science, etc. For example, the planets revolve in their orbits which are elliptical in shape.
In an atom, it is believed that, electrons revolve around the nucleus in elliptical orbits.
The concept of ellipses is used in medicine for treatment of kidney stones (lithotripsy). Other real-world examples of elliptical shapes are the huge elliptical park in front of the White House in Washington DC and the St. Paul’s Cathedral building.
Up to this point, you have got an idea of what an ellipse is, let’s now proceed by looking at how to calculate area of an ellipse.
How to Find the Area of an Ellipse?
To calculate the area of an ellipse, you need the measurements of both the major radius and minor radius.
Area of an ellipse formula
The formula for area of an ellipse is given as:
Area of an ellipse = πr1r2
Where, π = 3.14, r1 and r2 are the minor and the major radii respectively.
Note: Minor radius = semi -minor axis (minor axis/2) and the major radius = Semi- major axis (major axis/2)
Let’s test our understanding of the area of an ellipse formula by solving a few example problems.
Example 1
What is the area of an ellipse whose minor and major radii are, 12 cm and 7 cm, respectively?
Solution
Given;
r1 =7 cm
r2 =12 cm
By the formula,
Area of an ellipse = πr1r2
= 3.14 x 7 x 12
= 263.76 cm2
Example 2
The major axis and minor axis of an ellipse are, 14 m and 12 m, respectively. What is the area of the ellipse?
Solution
Given;
Major axis = 14m ⇒ major radius, r2 =14/2 = 7 m
Minor axis = 12 m ⇒ minor radius, r1 = 12/2 = 6 m.
Area of an ellipse = πr1r2
= 3.14 x 6 x 7
= 131.88 m2.
Example 3
The area of an ellipse is 50.24 square yards. If the major radius of the ellipse is 6 yards more than the minor radius. Find the minor and major radii of the ellipse.
Solution
Given;
Area = 50.24 square yards
Major radius = 6 + minor radius
Let the minor radius = x
Therefore,
The major radius = x + 6
But, area of an ellipse = πr1r2
⇒50.24 = 3.14 * x *(x + 6)
⇒50.24 = 3.14x (x + 6)
By applying the distributive property of multiplication on the RHS, we get,
⇒50.24 = 3.14x2 + 18.84x
Divide both sides by 3.14
⇒16 = x2 + 6x
⇒x2 + 6x – 16 =0
⇒x2 + 8x – 2x – 16 = 0
⇒ x (x + 8) – 2 (x + 8) = 0
⇒ (x – 2) (x + 8) = 0
⇒ x = 2 or – 4
Substitute x = 2 for the two equations of radii
Therefore,
The major radius = x + 6 ⇒ 8 yards
The minor radius = x = 2 yards
So, the major radius of the ellipse is 8 yards and the minor radius is 2 yards.
Example 4
Find the area of an ellipse whose radii area 50 ft and 30 ft respectively.
Solution
Given:
r1 = 30 ft and r2 = 50 ft
Area of an ellipse = πr1r2
A = 3.14 × 50 ×30
A = 4,710 ft2
Hence, the area of the ellipse is 4,710 ft2.
Example 5
Calculate the area of the ellipse shown below.
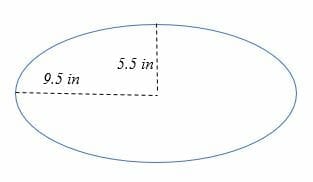
Solution
Given that;
r1 = 5.5 in
r2 = 9.5 in
Area of an ellipse = πr1r2
= 3.14 x 9.5 x 5.5
= 164.065 in2
Area of a semi – ellipse (h2)
A semi ellipse is a half an ellipse. Since we know the area of an ellipse as πr1r2, therefore, the area of a semi ellipse is half the area of an ellipse.
Area of a semi ellipse = ½ πr1r2
Example 6
Find the area of a semi – ellipse of radii 8 cm and 5 cm.
Solution
Area of a semi ellipse = ½ πr1r2
= ½ x 3.14 x 5 x 8
= 62.8 cm2.
