- Home
- >
- Coordinate Geometry – Explanation & Examples
Coordinate Geometry – Explanation and Examples
 Coordinate geometry is defined as the study of objects and shapes in a specified coordinate system.
Coordinate geometry is defined as the study of objects and shapes in a specified coordinate system.
Analytical geometry and Cartesian geometry are two other names for coordinate geometry. It is the opposite of pure geometry, which does not make use of any formulae or specific points on the Cartesian plane.
We will discuss various subtopics of coordinate geometry in this section, including:
- What is Coordinate Geometry?
- How to Do Coordinate Geometry
What is Coordinate Geometry?
Coordinate geometry is similar to pure geometry in that it focuses on objects like points, lines, and circles. Unlike pure geometry, however, it uses a reference system and units to define properties of these objects.
For example, in pure geometry, a point is simply “that which has no part,” and its existence will be postulated. In coordinate geometry, on the other hand, the location of a point relative to other points or objects is just as important as its existence.
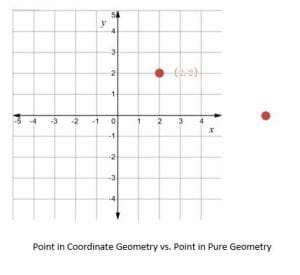
Because coordinate geometry uses units, it is possible to develop equations and formulae to relate objects and discover properties about objects. Some common examples include distance, area, and circumference.
Coordinate Geometry in Two Dimensions
Unless otherwise specified, coordinate geometry usually refers to two-dimensional coordinate geometry. The most common coordinate system used is the Cartesian coordinate system, which is sometimes called rectangular coordinates.
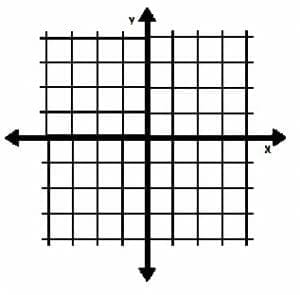
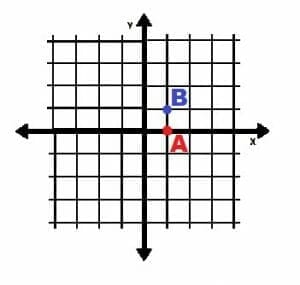
The Cartesian coordinate system has a horizontal axis called the x-axis and a vertical axis called the y-axis. These two axes meet at the origin. The expression (x, y) references a point in this system. Here, x is the horizontal distance from the origin and y is the vertical distance from the origin. A negative number signifies leftward or downward movement. On the other hand, a positive number specifies rightward or upward movement. The origin has coordinates (0, 0), while the point A in the image below has coordinates (1, 2).
Coordinate Geometry in Three Dimensions
Coordinate geometry is not limited to two dimensions! It is also possible to consider objects in three dimensional and even higher dimensions.
The coordinates (x, y, z) represent a point in three-dimensional space found by moving x units along the horizontal axis, y units along the vertical axis, and z units along a third axis.
Volume is an example of how we can use coordinate geometry in three dimensions.
How to Do Coordinate Geometry
Coordinate geometry encompasses many areas of mathematics. This includes finding properties of lines such as their length and their equations. It also includes finding the distances and angles between objects. Coordinate geometry can also make use of formulae to find geometric properties like area.
The basis for understanding any of these concepts is being able to develop and navigate a coordinate system.
How are Coordinate Systems Chosen?
Coordinate systems often map onto real-life objects. For example, geographic maps always feature coordinate systems. In them, latitude measures a vertical distance while longitude measures a horizontal distance. The origin — the point (0, 0) — of the latitude and longitude system is where the equator meets the line for 0 degrees longitude. This point is off of the coast of West Africa. Any measurement in latitude and longitude will use his point as a reference.
Artists, computer programmers, and engineers use coordinate systems all of the time in their work. The origin is typically a point that makes calculations simple or is easily identified.
Are there Other Types of Coordinate Systems?
Cartesian, or rectangular, coordinates are the most common type of coordinate system. In this system, the coordinates (x, y) refer to a point that is x units to the right of the origin and y units above the origin.
This is not, however, the only system out there. Another common system is the polar coordinate system. In it, the point (r, θ) refers to a point that is r units from the origin at an angle of θ from the right horizontal.
For example, in the image below, the point A is at (1, 0) in polar coordinates. The point B is at (√(2), 45) in polar coordinates.
In rectangular coordinates, A is still at the point (1, 0). B, however, is at the point (1, 1).
Cylindrical coordinates extend the concept of polar coordinates to three dimensional space. The coordinates (r, θ, z) represent a point that is r units from the origin at an angle of theta and a height of z.
Alternatively, spherical coordinates also represent objects in three-dimensional space. The coordinates (r, θ, φ) represent a point that is r units from the origin at an angle of theta along one axis and an angle of phi along another axis.
What are Quadrants
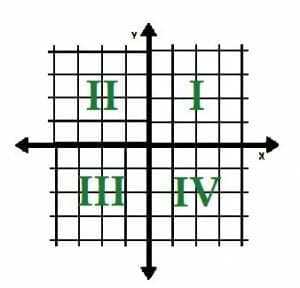
Quadrants are the four “zones” in the Cartesian coordinate system. They are separated from each other by the x and y axes.
Quadrant I has all positive coordinates. In quadrant II, x has negative coordinates while y has positive coordinates. Quadrant III has all negative coordinates, and quadrant IV has positive x coordinates and negative y coordinates. The quadrants are labelled in the image below.
Examples
This section includes common coordinate geometry practice problems and their detailed solutions.
Example 1
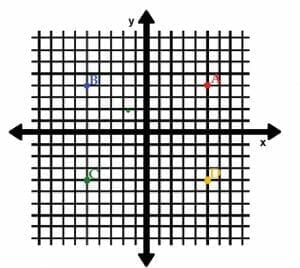
Find the following points in rectangular coordinates, then identify their quadrants:
A=(5, 4)
B=(-5, 4)
C=(-5, -4)
D=(5, -4)
Example 1 Solution
Recall that the first number in a pair of rectangular coordinates is the x-value. It indicates horizontal motion. The second number is the y-value. It indicates vertical motion.
The point A is (5, 4). This means that the point A is located 5 units to the right of the origin and 4 units upwards.
Since both the x and the y values are positive, the point A lies in the first quadrant.
The point B is (-5, 4). Since the x-value is negative, the point lies 5 units to the left of the origin. The y-value is still positive, so this point is also 4 units upwards.
This means the point B is in the second quadrant because its x-value is negative but its y-value is positive.
The point C is (-5, -4). Negative values mean that this point lies 5 units to the left and 4 units down from the origin.
The two negative values also indicate that the point C lies in the third quadrant.
Finally, the point D is (5, -4). This means it is 5 units to the right of the origin and 4 units down.
The point D has a positive x-value and a negative y-value, so it is in the fourth quadrant.
Example 2
Find the following points in polar coordinates. Assume that all theta values are given in radians.
A=(3, 0)
B=(1, π⁄3)
C=(2, π)
D=(1⁄2, π⁄2)
Example 2 Solution
Recall that polar coordinates include a radius and an angle. All points are found by first drawing a line of the given radial length from the origin to the right. Then, rotate that line by the angle given. The new end point of the line is the location of the point.
The point A is (3, 0). This means A is found be creating a line of length 3 units that starts at the origin and extends to the right along the horizontal.
Since the angle of rotation for this point is 0, the point is just the end point of the original line, as shown below.
The point B is (1, π⁄3). The means we start by drawing a line of length one that begins at the origin and extends to the right along the horizontal.
We then rotate this line counterclockwise around the origin by π⁄3 radians. The new endpoint of this line is the point B. Note, if you are familiar with trigonometry, that this point lies on the unit circle.
The point C is (2, π). As in the case of A and B, we start by making a line of length 2 that begins at the origin and extends to the right. Then, rotate this line π radians (180 degrees) counterclockwise about the origin. The new end point is 2 units to the left of the origin along the horizontal.
The point D is (1⁄2, π⁄2). First, create a line that has a length of 1⁄2 units that begins at the origin and extends to the right. Then, rotate this line π⁄2 radians counterclockwise about the origin. Then, since π⁄2=90 degrees, this point will be 1⁄2 units directly above the origin.
Example 3
Find the relationship between the two points A=(1, 2) and B=(-4, 3) in rectangular coordinates.
Example 3 Solution
It helps to first plot the points A and B on the coordinate plane.
The point A is (1, 2), so it is one unit to the right of and two units above the origin.
The point B is (-4, 3), so it is four units to the left of and three units above the origin.
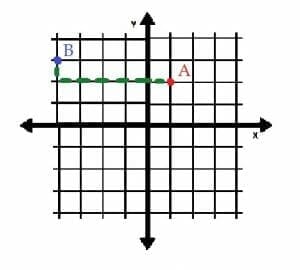
If the point B were moved to the point A, it would need to be moved five units to the right and one unit downwards. On the other hand, A could be placed at B by moving it up one unit and moving it five units to the left.
Example 4
The object shown below is contained in which quadrant(s)?
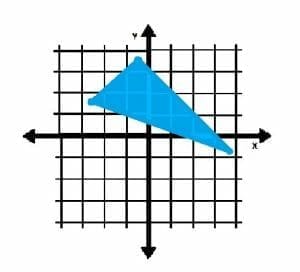
Example 4 Solution
The first quadrant is to the upper right of the origin. The other quadrants follow in order as you move around the coordinate plane counterclockwise.

Since the vertices of the triangle lie in quadrants II and IV, the object clearly has points in those two quadrants.
Some of the points on the interior of the triangle also lie in the first quadrant. Therefore, the answer is: quadrants I, II, and IV.
Example 5
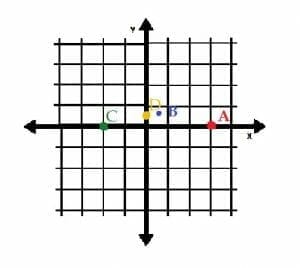
What are the rectangular coordinates of the points shown below?
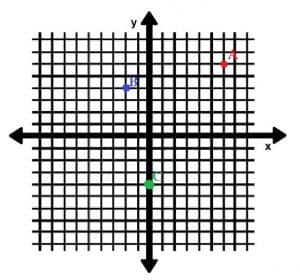
Example 5 Solution
To get from the origin to the point A, one needs to move the point six units to the right and six units up. Therefore, its position is (6, 6).
The point B is two units left of the origin, so its x-value is -2. It is also 4 units above the origin, so its y-value is 4. The coordinate pair is (-2, 4)
Finally, C lies on the y-axis. This means its x-value is zero. Since it is below the origin, its y-value is negative. Therefore, its coordinates are (0, -4).
