- Home
- >
- Spherical Coordinates – Definition, Graph, and Examples
JUMP TO TOPIC
Spherical Coordinates – Definition, Graph, and Examples
The spherical coordinates are used when estimating the surface area of figures such as cones and spheres that are defined in the three-dimensional coordinate system. The spherical coordinate system allows us to understand curves in space better. It allows us to rewrite expressions in terms of two angles and a distance in three-dimensional systems.
The spherical coordinate system is a three-dimensional coordinate system that models three-dimensional geometric figures using the radial distance, the zenith angle, and the azimuth angle.
Refresh your knowledge on Cartesian coordinate systems in 3D and the cylindrical coordinate systems to make the most out of the discussion. In this article, we’ll show you the important components of spherical coordinates and learn how to convert them from one coordinate system to another.
What Are Spherical Coordinates?
The spherical coordinates allow us to find the position of a point in $\mathbb{R}^3$ by using one distance and two angles: $\rho$, $\theta$, and $\varphi$, respectively.
- $\rho$ represents the distance of the point, $P$, from the origin
- $\theta$ represents the angle formed from the positive $x$-axis ($0\leq \theta \leq 2\pi$)
- $\varphi$ represents the angle formed between the $z$-axis and the line segment shown below ($0 \leq \varphi \leq \pi$)
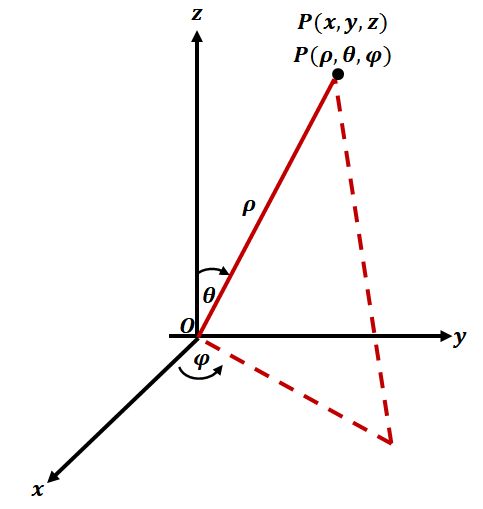
In the three-dimensional coordinate system, we use three axes: $x$, $y$, and $z$ axes. Each pair of axes will form the following planes: $xy$, $yz$, and $xz$ planes. Now, we define the spherical coordinate system by using a fixed point where the three coordinates meet. This common point is the origin. The second component needed in the spherical coordinate system is the zenith direction. It is the direction from the origin to the imaginary point (or zenith) that is above the origin.
When we have a point, $P = (r, \theta, \varphi)$, we call $\rho$ the radial distance or radius and it reflects the three-dimensional distance of $\boldsymbol{P}$ from the origin. The second coordinate, $\theta$, represents the polar angle and is formed from the zenith direction and the line connecting $\boldsymbol{P}$ and the origin. The third coordinate, $\varphi$, is called the azimuth angle and is formed by using a reference line along the plane that is perpendicular with the zenith direction.
To better understand the spherical coordinate system, let’s see how we can translate spherical coordinates to the two 3D coordinate systems that we know: rectangular and cylindrical coordinate systems.
How To Convert To Spherical Coordinates?
We can convert rectangular or cylindrical coordinates to spherical coordinates and vice-versa by using their respective definitions. The location of the spherical coordinates will be the same as its rectangular or cylindrical counterparts. This is why it’s important that we learn how to convert spherical coordinates to other coordinate systems.
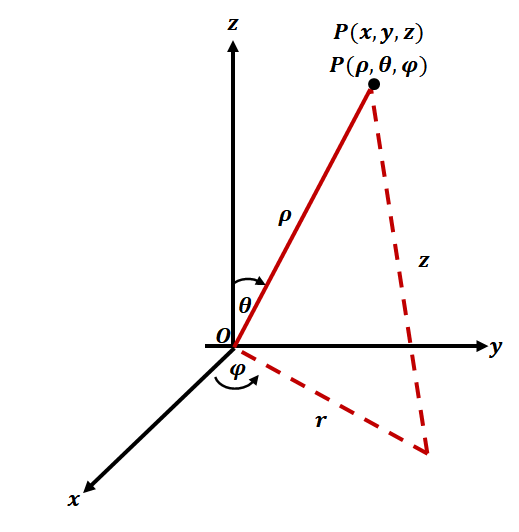
We can define the relationship between spherical and rectangular coordinates using the formulas shown below.
\begin{aligned}\textbf{Spherical} \rightarrow\textbf{Rectangular}\end{aligned} | \begin{aligned}\textbf{Rectangular} \rightarrow \textbf{Spherical}\end{aligned} |
\begin{aligned}x &= \rho \sin \varphi \cos \theta\\ y &= \rho \sin \varphi \sin \theta\\z &= \rho \cos \varphi\end{aligned} | \begin{aligned}\rho^2 &= x^2 + y^2 + z^2 \\\tan \theta &= \dfrac{y}{x}\\\varphi &= \cos^{-1} \left(\dfrac{z}{\sqrt{x^2 + y^2 + z^2}} \right )\end{aligned} |
At first glance, these formulas may look complicated but if we know that the segment formed by $r$ and the $z$-axis are perpendicular, so we can apply fundamental trigonometric identities. By quick inspection, we can confirm that $r = \rho \sin \varphi$. Looking at the $xy$-plane, we can also see that $x = r\cos \theta = \rho \sin \varphi \cos \varphi$. For the rest, you can try deriving on your own using trigonometric formulas.
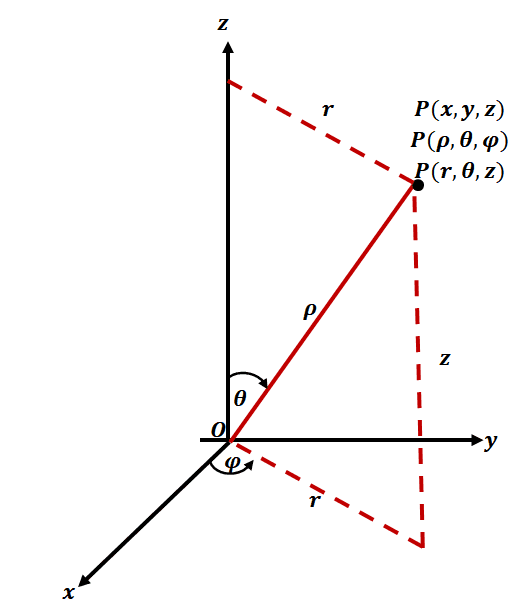
We’ve learned in the past that we can also convert cylindrical coordinate and rectangular coordinate systems; we can extend this to convert spherical to cylindrical coordinate systems as shown below.
\begin{aligned}\textbf{Spherical} \rightarrow \textbf{Cylindrical}\end{aligned} | \begin{aligned}\textbf{Cylindrical} \rightarrow \textbf{Spherical}\end{aligned} |
\begin{aligned}r &= \rho \sin \varphi\\ \theta &= \theta \\z &= \rho \cos \varphi\end{aligned} | \begin{aligned}\rho &= \sqrt{r^2 + z^2}\\\theta &= \theta \\\varphi &= \cos^{-1} \left(\dfrac{z}{\sqrt{r^2 + z^2}}\right)\end{aligned} |
Use these relationships to convert cylindrical to spherical coordinates. We’ll show you two examples of you how we can use these relationships to convert rectangular and cylindrical coordinates to spherical coordinates.
Rectangular Coordinate: $\boldsymbol{(2, 1, 2)}$ | Cylindrical Coordinate: $\boldsymbol{\left(4, \dfrac{\pi}{3}, \dfrac{\pi}{4}\right)}$ |
\begin{aligned}\rho^2 &= 2^2 + 1^2 + 2^2 \\\rho &= 3\\\tan \theta &= \dfrac{1}{2}\\\theta &=\tan^{-1}\left(\dfrac{1}{2} \right ) \\& \approx 26.57^{\circ}\\\varphi &= \cos^{-1} \left(\dfrac{2}{\sqrt{ 2^2 + 1^2 + 2^2}} \right )\\&= \cos^{-1} \left(\dfrac{2}{3}\right)\\& \approx 48.19^{\circ}\end{aligned} | \begin{aligned}r &= 4 \sin \dfrac{\pi}{4}\\&= 2\sqrt{2}\\ \theta &= \dfrac{\pi}{3} \\z &= 4 \cos \dfrac{\pi}{4}\\&= 2\sqrt{2}\end{aligned} |
This means that $(2, 1, 2)$ is equal to $(3, 26.57^{\circ}, 48.19^{\circ})$ in spherical coordinates. Similarly, $\left(4, \dfrac{\pi}{3}, \dfrac{\pi}{4}\right)$ is equal to $\left(2\sqrt{2}, \dfrac{\pi}{3}, 2\sqrt{2} \right)$ in spherical coordinate system.
How To Find Spherical Coordinates?
It’s much easier to find spherical coordinates by converting the point to rectangular coordinates first. Once we have the rectangular coordinate of the point, we can easily locate its position: $x$ units from the $x$-axis, $y$ units from the $y$-axis, and $z$ units from the $z$-axis.
For example, if we want to describe the position of $(2, 30^{\circ}, 60^{\circ})$, we first convert this spherical coordinate to rectangular coordinate as shown below.
\begin{aligned}\boldsymbol{x = \rho \sin \varphi \cos \theta}\end{aligned} | \begin{aligned}x &= 2 \sin 60^{\circ} \cos 30^{\circ}\\&= 1.5\end{aligned} |
\begin{aligned}\boldsymbol{y = \rho \sin \varphi \sin \theta}\end{aligned} | \begin{aligned}y &= 2 \sin 60^{\circ} \sin 30^{\circ}\\&= \dfrac{\sqrt{3}}{2}\\& \approx 0.866\end{aligned} |
\begin{aligned}\boldsymbol{z = \rho \cos \varphi }\end{aligned} | \begin{aligned}z &= 2 \cos 60^{\circ}\\&= 1 \end{aligned} |
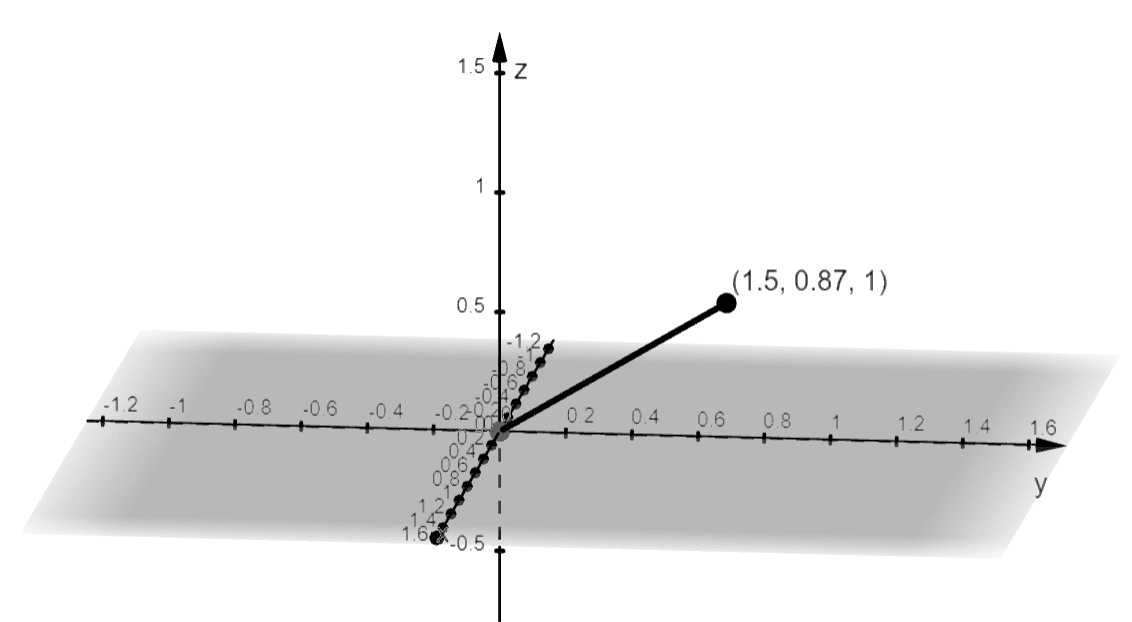
This means that $(2, 30^{\circ}, 60^{\circ})%%EDITORCONTENT%%nbsp; is equivalent to $(1.5, 0.87, 1)$ in rectangular coordinates. This means that it is $1.5$ units along the $x$-unit. From the $x$-axis, move $0.87$ unit in the positive direction and parallel to the $y$-axis. Lastly, move $1.73$ units along the direction that is parallel to the $z$-axis.
How To Graph Spherical Coordinates?
There are two ways to graph spherical coordinates: 1) directly plotting the spherical coordinate using their components and 2) converting the coordinates to rectangular coordinates then plotting the rectangular coordinate instead.
Plotting the Spherical Coordinate Directly
Here are helpful guidelines to keep in mind when plotting spherical coordinates using $\rho$, $\theta$, and $\varphi$:
- Use the projection of the point on the $xy$-plane as a guide.
- Sketch a reference segment connecting the projected point and make sure it forms an angle of $\theta$ along the $x$-axis.
- Sketch the line that is $\rho$ units long and forms angle of $\varphi$ from the $z$-axis.
- Sketch a line segment connecting the reference segment and the line.
- Plot the point on the intersection formed by the line segment and the line similar to our image from the first section.
This process may be tedious especially when you have no tools with you to estimate the angles. This is why we’ll recommend the second route: converting the spherical coordinates to rectangular coordinates first.
Plotting the Spherical Coordinate by Converting It To Rectangular Coordinate
- Convert the spherical coordinate to rectangular coordinate using the formula shown below:
\begin{aligned}x &= \rho \sin \varphi \cos \theta\\ y &= \rho \sin \varphi \sin \theta\\z &= \rho \cos \varphi\end{aligned}
- Use the rectangular coordinate, $(x, y, z)$, to graph the point.
For example, in our previous discussion, we’ve shown that $(2, 30^{\circ}, 60^{\circ})%%EDITORCONTENT%%nbsp; is equal to $(1.5, 0.87, 1)$. Graph the point by moving $1.5$ units along the $x$-axis then moving $0.87$ units along the positive direction of the $y$-axis. Plot the point by moving $1$ parallel to the positive $z$-axis.
Example 1
Convert the spherical coordinate, $(4, 45^{\circ}, 60^{\circ})$, to its cylindrical form.
Solution
Use the following formulas to find the components of the cylindrical coordinate that is equivalent to $(\rho, \theta, \varphi) = (4, 45^{\circ}, 60^{\circ})$.
\begin{aligned}r &= \rho \sin \varphi\\ \theta &= \theta \\z &= \rho \cos \varphi\end{aligned}
Hence, we have the following components for the cylindrical coordinate:
\begin{aligned}r = \rho \sin \varphi\end{aligned} | \begin{aligned}r &= 4\sin 60^{\circ}\\ &= 2\sqrt{3} \end{aligned} |
\begin{aligned}\theta = \theta\end{aligned} | \begin{aligned}\theta &= 45^{\circ} \end{aligned} |
\begin{aligned}z = \rho \cos \varphi \end{aligned} | \begin{aligned}z &= 4\cos 60^{\circ} \\&= 2\end{aligned} |
This means that the spherical coordinate, $(4, 45^{\circ}, 60^{\circ})$, is equivalent to $(2\sqrt{3}, 45^{\circ}, 2)$ in cylindrical form.
Example 2
Convert the spherical coordinate, $(2, 120^{\circ}, 30^{\circ})$, to its rectangular form then plot the point.
Solution
We have the following expressions for $(\rho, \theta, \varphi)$ in rectangular form, $(x, y, z)$:
\begin{aligned}x &= \rho \sin \varphi \cos \theta\\ y &= \rho \sin \varphi \sin \theta\\z &= \rho \cos \varphi\end{aligned}
This means that $(2, 120^{\circ}, 30^{\circ})$ has the following rectangular coordinates as shown below.
\begin{aligned}x = \rho \sin \varphi \cos \theta\end{aligned} | \begin{aligned}x &= 2 \sin 30^{\circ} \cos 120^{\circ}\\&= -\dfrac{1}{2}\end{aligned} |
\begin{aligned}y = \rho \sin \varphi \sin \theta\end{aligned} | \begin{aligned}y &= 2 \sin 30^{\circ} \sin 120^{\circ}\\&= \dfrac{\sqrt{3}}{2}\end{aligned} |
\begin{aligned}z = \rho \cos \varphi \end{aligned} | \begin{aligned}z &= 2 \cos 30^{\circ}\\&= \sqrt{3}\end{aligned} |
This means that the spherical coordinate is equivalent to $\left(-\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}, \sqrt{3}\right)$ or approximately $(-0.5, 0.87, 1.73)$. Use the rectangular form to graph the spherical coordinate, $(2, 120^{\circ}, 30^{\circ})$.
- Move $0.5$ unit along the negative $x$-axis.
- From the $x$-axis, move $0.87$ unit parallel to the positive $y$ direction.
- Now, move $1.73$ units above the origin and along the $z$-axis.
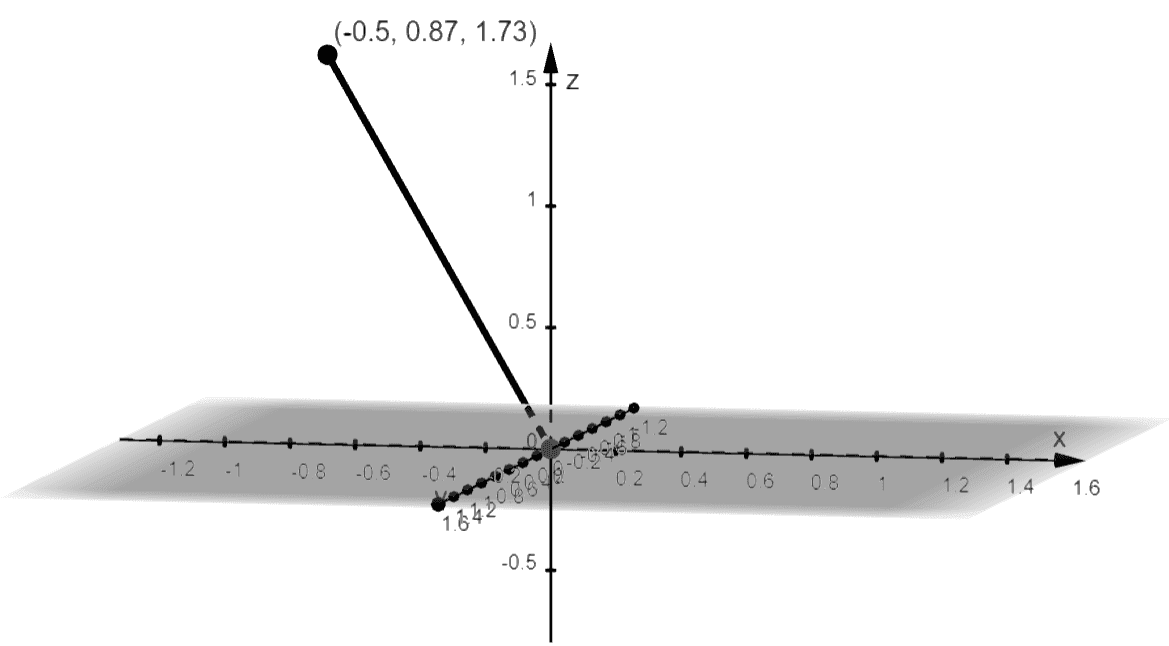
Here’s the graph of the spherical coordinate using its rectangular form.
Practice Questions
1. Convert the following spherical coordinates to their cylindrical forms.
a. $(6, 30^{\circ}, 30^{\circ})$
b. $\left(12, 120^{\circ}, 60^{\circ}\right)$
c. $\left(16, \dfrac{3\pi}{4}, \dfrac{\pi}{4}\right)$
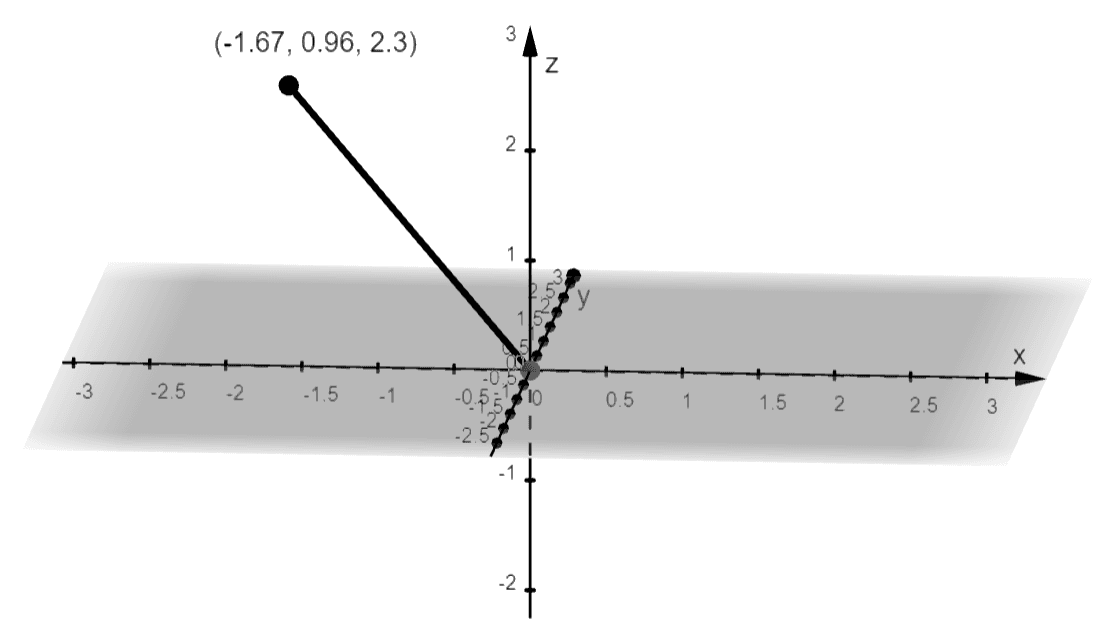
2. Convert the spherical coordinate, $(3, 150^{\circ}, 40^{\circ})$, to its rectangular form then plot the point.
Answer Key
1.
a. $(3, 30^{\circ}, 3\sqrt{3})$
b. $(6\sqrt{3}, 120^{\circ}, 6)$
c. ty}$\left(8\sqrt{2}, \dfrac{3\pi}{4}, 8\sqrt{2} \right)$
2. $(3, 150^{\circ}, 40^{\circ}) = (-1.67, 0.96, 2.30)$
3D images/mathematical drawings are created with GeoGebra.
