Area of Circle – Explanation & Examples

To recall, the area is the region that occupied the shape in a two-dimensional plane. In this article, you will learn the area of a circle and the formulas for calculating the area of a circle.

What is the Area of a Circle?

The area of the circle is the measure of the space or region enclosed inside the circle. In simple words, the area of a circle is the total number of square units inside that circle.

For example, if you draw squares of dimensions 1cm by 1cm inside a circle. Then, the total number of full squares located inside the circle represents the area of the circle. We can measure the area of a circle in m², km², in², mm^2, etc.

Formula for the Area of a Circle

The area of a circle can be calculated using three formulas. These formulas are applied depending on the information you are given.

Let us discuss these formulas for finding the area of a circle.

Area of a circle using the radius

Given the radius of a circle, the formula for calculating the area of a circle states that:

Area of a Circle = πr² square units

A = πr² square units

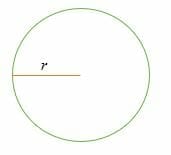
Where A = the area of a circle.

pi (π) = 22/7 or 3.14 and r = the radius of a circle.

Let’s get a better understanding of this formula by working out a few example problems.

Example 1

Find the area of a circle whose radius is 15 mm.

Solution

A = πr² square units

By substitution,

A = 3.14 x 15²

= (3.14 x 15 x 15) mm²

= 706.5 mm²

So, the area of the circle is 706.5 mm²

Example 2

Calculate the area of the circle shown below.

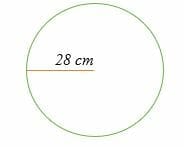
Solution

A = πr² square units

= (3.14 x 28²) cm²

= (3.14 x 28 x 28) cm²

= 2461.76 cm²

Example 3

The area of a circle is 254.34 square yards. What is the radius of the circle?

Solution

A = πr² square units

254.34 = 3.14 x r²

Divide both sides by 3.14.

r² = 254.34/3.14 = 81

Find the square root of both sides.

√r² = √81

r = -9, 9

Since the radius cannot have a negative value, we take positive 9 as the correct answer.

So, the radius of the circle is 9 yards.

Example 4

Lawn sprinkler sprays water 10 feet in every direction as it rotates. What is the area of the sprinkled lawn?

Solution

Here, the radius is 10 feet.

A = πr² square units

= 3.14 x 10²

= (3.14 x 10 x 10) sq. ft

= 314 sq. ft

Therefore, the area of the sprinkled lawn is 314 sq. ft.

Area of a circle using the diameter

When the diameter of a circle is known, the area of the circle is given by,

Area of a Circle = πd²/4 square units

Where d = the diameter of a circle.

Example 5

Find the area of a circle with a diameter of 6 inches.

Solution

A = πd²/4 square units

= 3.14 x 6²/4 Sq. inches.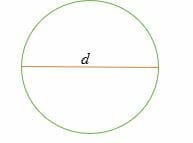

= (3.14 x 6 x 6)/4 Sq. inches

= 28.26 sq. inches

So, the area of the circle with a diameter of 6 inches is 28.26 square inches.

Example 6

Calculate the area of the circle shown below.

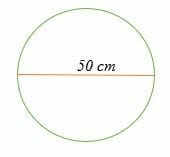
Solution

Given the diameter,

A = πd²/4 square units

= 3.14 x 50²/4

= (3.14 x 50 x 50)/4

=1962.5 cm²

Example 7

Calculate the area of a dinner plate, which has a diameter of 10 cm.

Solution

A = πd²/4 square units

= 3.14 x 10²/4

= (3.14 x 10 x 10)/4

= 78.5 cm²

Example 8

The diameter of a circular plate is 20 cm. Find the dimensions of a square plate that will have the same area as the circular plate.

Solution

Equate the area of the circle to the area of the square

πd²/4 = s²

3.14 x 20²/4 = s²

s² =314

Find the square root of both sides to get,

s = 17.72

Therefore, the dimensions of the square plate will be 17.72 cm by 17.72 cm.

Example 9

Find the diameter of a circle with an area of 156 m².

Solution

A = πd²/4

156 = 3.14d²/4

Multiply both sides by 4.

624 = 3.14d²

Divide both sides by 3.14.

198.726 = d²

d = 14.1 m

Thus, the diameter of the circle will be 14.1 m.

Area of a circle using the circumference

As we already know, the circumference of a circle is the distance around a circle. It is possible to calculate the area of a circle given its circumference.

Area of a circle = C²/4π

A = C²/4π

Where C = the circumference of a circle.

Example 10

Find the area of a circle whose circumference is 25.12 cm.

Solution

Given the circumference,

Area = C²/4π

A = 25.12²/4π

= 50.24 cm²

Example 11

What is the circumference of a circle whose area is 78.5 mm²?

Solution

A = C²/4π

78.5 = C²/4π

Multiply both sides by 4π.

C² = 985.96

Find the square root of both sides.

C = 31.4 mm.

So, the circumference of the circle is 31.4 mm.