Circumference of a Circle – Explanation & Examples

We saw before how to find the perimeter of the polygon. We know that circle is not a polygon. Therefore, it should not have a perimeter. We use an equivalent form for a circle, called circumference.

In this article, we will discuss how to find a circle’s circumference, the circumference of a circle formula, examples, and sample problems about the circumference of a circle.

What is the circumference of a circle?

The distance around a polygon, such as a square or a rectangle, is called the perimeter (P).  On the other hand, the distance around a circle is referred to as the circumference (C). Therefore, the circumference of a circle is the linear distance of an edge of the circle.

Why do we do need to calculate the circumference of a circle?

Finding the circumference of an object is important in the following scenarios:

Whether you want to buy a bra, trouser, or sweater, you need to know the distance around your waist or chest. Though your body isn’t a perfect circle, you will have to measure its circumference using a tape measure. Tailors mostly use this technique to determine the circumference of a dress.

You also need to know the circumference of a circle doing craftwork, putting fencing around your hot tub, or just solving a math problem for school.

How to find the circumference of a circle?

As stated before, the perimeter or circumference of a circle is the distance around a circle or any circular shape. The circumference of a circle is the same as the length of a straight line folded or bent to make the circle. The circumference of a circle is measured in meters, kilometers, yards, inches, etc.

There are two ways of finding the perimeter or circumference of a circle. The first formula involves using the radius, and the second involves using the diameter of a circle. It is important to note that both two methods yield the same result.

Let’s take a look.

The circumference of a circle is given by;

C = 2 * π* R = 2πR

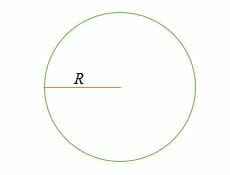
where,

C = Circumference or perimeter,

R = the radius of a circle,

π = the mathematical constant known as Pi

Or

C = π* D = π D

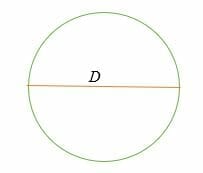
where, D = 2R = The diameter of a circle

For any circle, its circumference ratio to its diameter is equal to a constant known as pi.

Circumference/Diameter = Pi

C /D = Pi or C/2R = pi

The approximate value of pi (π) = 22/7 = 3.1415926535897…. (a non-terminating value)

For the easier computation of a circle’s circumference, pi’s value is taken to be 3.14 (π = 3.14).

Let’s see a few examples below to polish the concept of the circumference.

Example 1

Find the circumference of the circle with a radius of 8 cm.

Solution

Circumference = 2 * π* R = 2πR

= 2 * 3.14 * 8

= 50.24 cm.

Example 2

Calculate the circumference of a circle whose diameter is 70 mm

Solution

Circumference = π* D = π D

= 3.14 * 70

= 219.8 mm

Example 3

Calculate the perimeter of a circular flower garden whose radius is 10 m.

Solution

Circumference = 2 * π* R = 2πR

= 2 * 3.14 * 10

= 62.8 m.

Example 4

The circumference of a circle is 440 yards. Find the diameter and radius of the circle.

Solution

Circumference = 2 * π* R = 2πR

440 =2 * 3.14 * R

440 = 6.28R

Divide both sides by 6.28 to get,

R = 70.06

Therefore, the radius of the circle is 70.06 yards. But, since the diameter is twice the radius of a circle, the diameter is equal to 140.12 yards.

Example 5

The diameter of the wheels of a bicycle is 100 cm. How many revolutions will each wheel make to travel a distance of 157 meters?

Solution

Calculate the circumference of the bicycle’s wheel.

Circumference = π D

= 3.14 * 100

= 314 cm

To get the number of revolutions of the wheel, divide the distance covered by the circumference of the wheel.

We need to convert 157 meters to cm before dividing, so we multiply 157 by 100 to get 15700 cm. Therefore,

Number of revolutions = 15700 cm/314 cm

= 50 revolutions.

Example 6

A piece of a wire in the form of a rectangle of length 100 cm and width 50 cm is cut and folded to make a circle. Calculate the circumference and radius of the circle formed.

Solution

The circumference of the circle formed = the perimeter of the rectangular wire.

Perimeter of a rectangle = 2(L + W)

= 2(100 + 50) cm

= 2 * 150 cm

= 300 cm.

Therefore, the circumference of the circle will be 300 cm.

Now calculate its radius.

Circumference = 2 π R

300 cm = 2 * π * R

300 cm = 2 * 3.14 * R

300 cm = 6.28R

Divide both sides by 6.28.

R = 47.77 cm

So, the radius of the circle will be 47.77 cm.

Example 7

The radius of each wheel of a motorcycle is 0. 85 m. How far will the motorcycle move if each wheel takes 1000 revolutions? Assume the motorcycle is moving on a straight line.

Solution

First, find the circumference of the wheel.

Circumference = 2 π R

= 2 * 3.14 * 0.85

= 5.338 m.

To find the distance traveled, multiply the circumference of the wheel by the number of revolutions taken.

Distance = 5.338 * 1000

= 5338 m

Therefore, the distance traveled is equal to 5.338 kilometers.