Common Difference – Formula, Explanation, and Examples
Learning about common differences can help us better understand and observe patterns. When working with arithmetic sequence and series, it will be inevitable for us not to discuss the common difference.
The common difference reflects how each pair of two consecutive terms of an arithmetic series differ.
In this article, we’ll understand the important role that the common difference of a given sequence plays. We’ll learn about examples and tips on how to spot common differences of a given sequence.
We’ll also explore different types of problems that highlight the use of common differences in sequences and series. This is why reviewing what we’ve learned about arithmetic sequences is essential.
For now, let’s begin by understanding how common differences affect the terms of an arithmetic sequence.
What is the common difference?
The common difference is an essential element in identifying arithmetic sequences. These are the shared constant difference shared between two consecutive terms.
Why don’t we take a look at the two examples shown below?
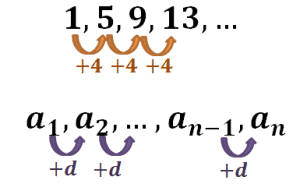
Why don’t we take a look at the two examples shown below?
- For the first sequence, each pair of consecutive terms share a common difference of $4$.
- The second sequence shows that each pair of consecutive terms share a common difference of $d$.
In general, when given an arithmetic sequence, we are expecting the difference between two consecutive terms to remain constant throughout the sequence.
Common difference definition
Let’s say we have an arithmetic sequence, $\{a_1, a_2, a_3, …, a_{n-1}, a_n\}$, this sequence will only be an arithmetic sequence if and only if each pair of consecutive terms will share the same difference.
We call this the common difference and is normally labelled as $d$. This means that if $\{a_1, a_2, a_3, …, a_{n-1}, a_n\}$ is an arithmetic sequence, we have the following:
\begin{aligned} a_2 – a_1 &= d\\ a_3 – a_2 &= d\\.\\.\\.\\a_n – a_{n-1} &=d \end{aligned}
We can use the definition we’ve discussed in this section when finding the common difference shared by the terms of a given arithmetic sequence.
How to find the common difference?
When given some consecutive terms from an arithmetic sequence, we find the common difference shared between each pair of consecutive terms.
Let’s say we have $\{8, 13, 18, 23, …, 93, 98\}$. We can find the common difference by subtracting the consecutive terms. We can confirm that the sequence is an arithmetic sequence as well if we can show that there exists a common difference.
\begin{aligned} 13 – 8 &= 5\\ 18 – 13 &= 5\\23 – 18 &= 5\\.\\.\\.\\98 – 93 &= 5\end{aligned}
This shows that the sequence has a common difference of $5$ and confirms that it is an arithmetic sequence.
We can also find the fifth term of the sequence by adding $23$ with $5$, so the fifth term of the sequence is $23 + 5 = 28$.
What if we’re given limited information and need the common difference of an arithmetic sequence?
Common difference formula
We might not always have multiple terms from the sequence we’re observing. However, we can still find the common difference of an arithmetic sequence’s terms using the different approaches as shown below.
Here are helpful formulas to keep in mind, and we’ll share some helpful pointers on when it’s best to use a particular formula.
$d = a_{k + 1}– a_k$
This formula for the common difference is most helpful when we’re given two consecutive terms, $a_{k + 1}$ and $a_k$. This also shows that given $a_k$ and $d$, we can find the next term using $a_{k + 1} = a_k + d$.
$d = \dfrac{a_n – a_1}{n – 1} $
This formula for the common difference is best applied when we’re only given the first and the last terms, $a_1 and a_n$, of the arithmetic sequence and the total number of terms, $n$.
We’ll learn how to apply these formulas in the problems that follow, so make sure to review your notes before diving right into the problems shown below.
Example 1
Find the common difference of the following arithmetic sequences.
a. $\{4, 11, 18, 25, 32, …\}$
b. $\{-20, -24, -28, -32, -36, …\}$
c. $\left\{\dfrac{1}{2}, \dfrac{3}{2}, \dfrac{5}{2}, \dfrac{7}{2}, \dfrac{9}{2}, … \right\}$
d. $\left\{-\dfrac{3}{4}, -\dfrac{1}{2}, -\dfrac{1}{4},0,…\right\}$
Solution
Each arithmetic sequence contains a series of terms, so we can use them to find the common difference by subtracting each pair of consecutive terms.
Let’s start with $\{4, 11, 18, 25, 32, …\}$:
\begin{aligned} 11 – 4 &= 7\\ 18 – 11 &= 7\\25 – 18 &= 7\\32 – 25&= 7\\.\\.\\.\\d&= 7\end{aligned}
This means that the common difference is equal to $7$.
Moving on to $\{-20, -24, -28, -32, -36, …\}$, we have:
\begin{aligned} -24 – (-20) &= -4\\ -28 – (-24) &= -4\\-32 – (-28) &= -4\\-36 – (-32) &= -4\\.\\.\\.\\d&= -4\end{aligned}
Hence, the second sequence’s common difference is equal to $-4$.
Let’s go ahead and check $\left\{\dfrac{1}{2}, \dfrac{3}{2}, \dfrac{5}{2}, \dfrac{7}{2}, \dfrac{9}{2}, … \right\}$:
\begin{aligned} \dfrac{3}{2} – \dfrac{1}{2} &= 1\\ \dfrac{5}{2} – \dfrac{3}{2} &= 1\\ \dfrac{7}{2} – \dfrac{5}{2} &= 1\\ \dfrac{9}{2} – \dfrac{7}{2} &= 1\\.\\.\\.\\d&= 1\end{aligned}
This means that third sequence has a common difference is equal to $1$.
Working on the last arithmetic sequence,$\left\{-\dfrac{3}{4}, -\dfrac{1}{2}, -\dfrac{1}{4},0,…\right\}$,we have:
\begin{aligned} -\dfrac{1}{2} – \left(-\dfrac{3}{4}\right) &= \dfrac{1}{4}\\ -\dfrac{1}{4} – \left(-\dfrac{1}{2}\right) &= \dfrac{1}{4}\\ 0 – \left(-\dfrac{1}{4}\right) &= \dfrac{1}{4}\\.\\.\\.\\d&= \dfrac{1}{4}\end{aligned}
Hence, the fourth arithmetic sequence will have a common difference of $\dfrac{1}{4}$.
Example 2
Which of the following terms can’t be part of an arithmetic sequence?
a. $11, 14, 17$
b. $-36, -39, -42$
c.$-\dfrac{1}{2}, \dfrac{1}{2}, \dfrac{5}{2}$
d. $-4 \dfrac{1}{4}, -2 \dfrac{1}{4}, \dfrac{1}{4}$
Solution
As we have mentioned, the common difference is an essential identifier of arithmetic sequences. If the sequence of terms shares a common difference, they can be part of an arithmetic sequence.
Starting with $11, 14, 17$, we have $14 – 11 = 3$ and $17 – 14 = 3$. This shows that the three sequences of terms share a common difference to be part of an arithmetic sequence.
Moving on to $-36, -39, -42$, we have $-39 – (-36) = -3$ and $-42 – (-39) = -3$. This means that they can also be part of an arithmetic sequence.
As for $-\dfrac{1}{2}, \dfrac{1}{2}, \dfrac{3}{2}$, we have $\dfrac{1}{2} – \left(-\dfrac{1}{2}\right) = 1$ and $\dfrac{5}{2} – \dfrac{1}{2} = 2$. Since their differences are different, they can’t be part of an arithmetic sequence.
For the fourth group, $-4 \dfrac{1}{4}, -2 \dfrac{1}{4}, \dfrac{1}{4}$, we can see that $-2 \dfrac{1}{4} – \left(- 4 \dfrac{1}{4}\right) = 2$ and $- \dfrac{1}{4} – \left(- 2 \dfrac{1}{4}\right) = 2$. This means that the three terms can also be part of an arithmetic sequence.
Hence, $-\dfrac{1}{2}, \dfrac{1}{2}, \dfrac{5}{2}$ can never be part of an arithmetic sequence.
Example 3
The first and the last terms of an arithmetic sequence are $9$ and $14$, respectively. If the sequence contains $100$ terms, what is the second term of the sequence?
Solution
When given the first and last terms of an arithmetic sequence, we can actually use the formula, $d = \dfrac{a_n – a_1}{n – 1}$, where $a_1$ and $a_n$ are the first and the last terms of the sequence. We also have $n = 100$, so let’s go ahead and find the common difference, $d$.
\begin{aligned}d &= \dfrac{a_n – a_1}{n – 1}\\&=\dfrac{14 – 5}{100 – 1}\\&= \dfrac{9}{99}\\&= \dfrac{1}{11}\end{aligned}
The first and the second term must also share a common difference of $\dfrac{1}{11}$, so the second term is equal to $9 \dfrac{1}{11}$ or $\dfrac{100}{11}$.
Example 4
Consider the arithmetic sequence, $\{4a + 1, a^2 – 4, 8a – 4, 8a + 12,… \}$, what could $a$ be?
Solution
For the sequence, $\{4a + 1, a^2 – 4, 8a – 4, 8a + 12,… \}$, to be an arithmetic sequence, they must share a common difference.
The common difference between the third and fourth terms is as shown below.
\begin{aligned}8a + 12 – (8a – 4)&= 8a + 12 – 8a – (-4)\\&=0a + 16\\&= 16\end{aligned}
In terms of $a$, we also have the common difference of the first and second terms shown below.
\begin{aligned}a^2 – 4 – (4a +1) &= a^2 – 4 – 4a – 1\\&=a^2 – 4a – 5\end{aligned}
Since these terms all belong in one arithmetic sequence, the two expressions must be equal. Equate the two and solve for $a$.
\begin{aligned}a^2 – 4a – 5 &= 16\\a^2 – 4a – 21 &=0 \\(a – 7)(a + 3)&=0\\\\a&=7\\a&=-3\end{aligned}
This means that $a$ can either be $-3$ and $7$.
